LinearModelFit

LinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]

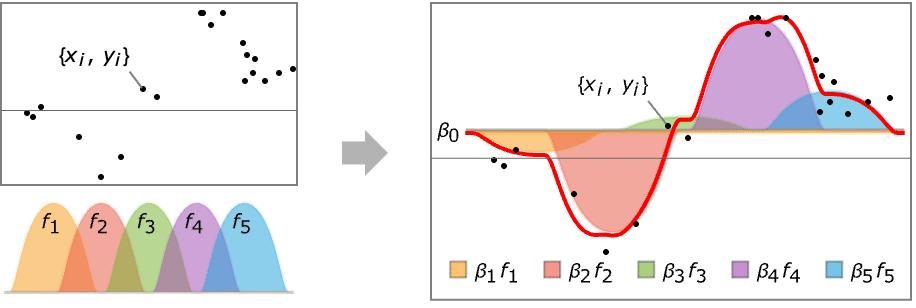
构建形为 的线性模型，拟合连续 xi 值的 yi.

LinearModelFit[data,{f1,f2,…},{x1,x2,…}]

构建线性模型，其中 fi 依赖于变量 xk.

LinearModelFit[{m,v}]

从设计矩阵 m 和响应向量 v 构建一个线性模型.

更多信息和选项

  • LinearModelFit 试图使用函数的线性组合对输入数据建模.
  • LinearModelFit 给出形为 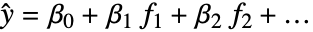的线性模型，假定原来的 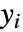是独立的正态分布，具有均值 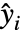和常见标准差.
  • LinearModelFit 返回符号 FittedModel 对象，用来表示构建的线性模型.
  • LinearModelFit 在特定点 x1、… 的最佳拟合函数的值可以从 model[x1,…] 得到.
  • data 的可能的形式为：
  • {y1,y2,…}与形式 {{1,y1},{2,y2},…} 等价
    {{x11,x12,…,y1},…}独立值 xij 列表和响应 yi
    {{x11,x12,…}y1,…}输入值和响应构成的规则列表
    {{x11,x12,…},…}{y1,y2,…}输入值列表和响应构成的规则
    {{x11,…,y1,…},…}n拟合矩阵的第 n 列
  • 在多元数据的情况下，如 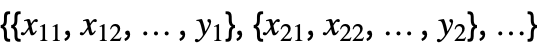{{x_(11),x_(12),... ,y_(1)},{x_(21),x_(22),... ,y_(2)},...}，坐标 xi1, xi2, … 的数量应等于变量 xi 的数量.
  • 数据点可以是近似实数. 不确定性可以用 Around 指定.
  • 另外，可用设计矩阵指定 data，不指定函数和变量：
  • {m,v}设计矩阵 m 和响应向量 v
  • 在 LinearModelFit[{m,v }] 中，设计矩阵 m 是由数据点上的基函数 fi 的值形成的，其形式为 {{f1,f2,…},{f1,f2,…},…}. 响应向量 v 是响应列表 {y1,y2,…}.
  • 使用设计矩阵时，可用 LinearModelFit[{m,v},{f1,f2,…}] 指定基函数 fi.
  • 对于设计矩阵 m 和响应向量 v，模型为 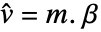，其中 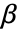是要估计的参数向量.
    • 选项
  • LinearModelFit 采用下列选项：
  • ConfidenceLevel 95/100参数和预测的置信度
    IncludeConstantBasis True是否包含一个常基函数
    LinearOffsetFunction None线性预测值的已知偏移
    NominalVariables None名义变量或分类变量
    VarianceEstimatorFunction Automatic起到随机变量的效果，而不是固定效果
    Weights Automatic数据元素的权
    WorkingPrecision Automatic内部计算的精度
  • 设置 IncludeConstantBasis->False，拟合模型形式为 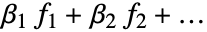. 如果设计矩阵已在输入文件中指定，则忽略 IncludeConstantBasis 选项.
  • 设置 LinearOffsetFunction->h，拟合形式为 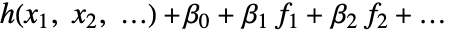的一个模型.
  • 在 ConfidenceLevel->p 下，对参数和预测区间计算概率-p 的置信区间.
  • 设置 Weights->{w1,w2,…}，yi 的误差方差假定与 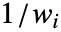成正比.
  • 设置 Weights->Automatic，如果数据包含精确值，权重将设为 1. 如果数据包含 Around 值，权重将设置为 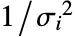，其中 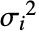为总响应方差.
  • 总响应方差 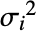是初始响应方差 si2 和独立值方差 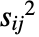的函数.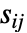
  • 使用 AroundReplace 在模型中传播，得到的方差与响应方差 si2 相加. 内部使用函数 FindRoot 根据 Fasano 和 Vio 方法找到自洽解.
  • 设置 VarianceEstimatorFunction->f，方差通过 f[res,w] 估计，其中 res={y1-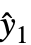,y2-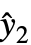,…} 是残差列表，w={w1,w2,…} 是测量 yi 权列表.
  • 用 VarianceEstimatorFunction->(1&) 和 Weights->{1/Δy12,1/Δy22,…}， Δyi 视为已知的测量不确定度 yi，参数标准误差实际上仅从权计算.
    • 属性
  • FittedModel 的属性和诊断信息可从 model["property"] 中获取.
  • 用 model["property"] 得到的数据和拟合函数的属性包括：
  • "BasisFunctions"基本函数列表
    "BestFit"拟合函数
    "BestFitParameters"参数估计
    "Data"输入数据或设计矩阵和响应向量
    "DesignMatrix"模型的设计矩阵
    "Function"最佳拟合的纯函数
    "Response"输入数据中的响应值
    "Weights"用于拟合数据的权重
  • 残差类型包括：
  • "FitResiduals"具体响应和预测响应的差异
    "StandardizedResiduals"通过除以每个残差的标准误差的拟合残差
    "StudentizedResiduals"通过除以单个删除误差估计的拟合残差
  • 与平方误差的和相关的属性包括：
  • "ANOVA"方差分析数据
    "CoefficientOfVariation"响应均值除以估计的标准偏差
    "EstimatedVariance"误差方差的估计
    "PartialSumOfSquares"删除模型平方和的变化
    "SequentialSumOfSquares"按组件分隔的模型平方和
  • 参数估计的属性包括：
  • "CorrelationMatrix"渐近线的参数相关矩阵
    "CovarianceMatrix"渐近线的参数协方差矩阵
    "Eigenstructure"参数相关矩阵的特征结构
    "ParameterEstimates"拟合参数信息表
    "VarianceInflationFactors"估计参数的膨胀因子列表
  • 影响度量的相关属性包括：
  • "BetaDifferences"参数值的影响度的 DFBETAS 测量
    "CatcherMatrix"catcher 矩阵
    "CookDistances"库克距离列表
    "CovarianceRatios"观察影响的 COVRATIO 测量
    "DurbinWatsonD"自相关的 Durbin–Watson 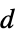统计
    "FitDifferences"预期值的影响度的 DFFITS 测量
    "FVarianceRatios"观察影响的 FVARATIO 测量
    "HatDiagonal"帽子矩阵的对角元素
    "SingleDeletionVariances"方差估计列表，忽略第 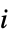个数据点
  • 预期值的属性包括：
  • "MeanPredictionBands"均值预期的置信带
    "MeanPredictions"平均预测值的置信区间
    "PredictedResponse"数据的拟合值
    "SinglePredictionBands"基于单个观察值的置信带
    "SinglePredictions"单一观测值预测响应的置信区间
  • 拟合优度度量的属性包括：
  • "AdjustedRSquared"模型参数数量的 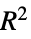调整
    "AIC"Akaike 信息标准
    "AICc"有限样本校正 AIC
    "BIC"Bayesian 信息标准
    "RSquared"决定系数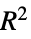
  • 对于属性 "RSquared" 和 "AdjustedRSquared"，平方的的总和计算仅在包括常数基础时进行平均调整.
  • "PredictedResponse"数据的拟合值
    "SinglePredictionBands"基于单一观测值的置信区间

范例

打开所有单元关闭所有单元

基本范例  (1)

拟合某些数据的一个线性模型：

查看模型的函数形式：

在某个点的计算：

可视化显示拟合函数：

提取拟合的信息：

绘制残差：

范围  (17)

数据  (7)

拟合单变量的模型，假设增大的整数独立数值：

这相当于：

拟合多变量模型，假设响应是最后一个变量：

这相当于：

指定一列数据作为响应：

拟合规则列表：

拟合输入值列表和响应构成的规则：

拟合有分类预期变量的模型：

拟合给出设计矩阵和响应向量的模型：

拟合关于 x 和 y 的基函数的模型：

模型  (3)

求函数的最佳拟合线性系数：

将数据拟合为自变量线性函数的线性组合：

这相当于明确指定常量函数：

将数据拟合为自变量非线性函数的线性组合：

属性  (7)

数据 & 拟合函数  (1)

拟合一个线性模型：

获取线性模型的可用属性列表：

提取原数据：

获取并绘制最优拟合：

获取纯函数形式的拟合函数：

获取所得拟合的设计矩阵和响应向量：

残差  (1)

检查拟合的残差：

可视化显示原拟合残差：

在图形中显示尺度残差：

绘制标准化残差和 Studentized 残差的绝对误差：

平方和  (1)

拟合某些数据的一个线性模型：

提取估计误差方差和变化系数：

获取模型的方差分析表：

从表中得到F统计：

参数估计诊断  (1)

得到参数信息的一个格式化表格：

获取拟合参数的 统计量：

影响度量  (1)

拟合包含极值的一个线性模型：

用单个删除方差，检测消去每个点的误差方差的影响：

检测库克距离，识别更高的影响点：

用 DFFITS 值估计每个拟合值的影响：

用 DFBETAS 值估计每个估计参数上每个点的影响：

预期值  (1)

拟合一个线性模型：

绘制与估计值相应预期值：

获取平均预测置信区间的表格式结果：

获取单一预测置信区间的表格式结果：

得到单个预期区间：

提取 99% 均值预期带：

拟合优度度量  (1)

得到一个线性模型的拟合优度：

计算所有线性子模型的拟合优度：

通过 排列模型：

调整 排列模型，改变增加项的顺序：

推广和延伸  (1)

在模型的函数形式上执行其它的数学操作：

符号积分和数值积分：

求出一个预期值，得到模型的一个特定值：

选项  (11)

ConfidenceLevel  (1)

缺省给出95%置信区间：

用 99% 的置信区间：

在 FittedModel 中设置级别为 90%：

IncludeConstantBasis  (1)

拟合一个简单的线性回归模型：

拟合有截断零的线性模型：

LinearOffsetFunction  (1)

拟合一个线性模型的数据：

拟合有已知 Sqrt[x] 项的线性模型：

NominalVariables  (1)

拟合数据，将第一个变量视为名义变量：

将所有变量视为名义变量：

VarianceEstimatorFunction  (1)

用缺省的无偏差估计：

假设一个已知的误差方差：

通过均值平方误差估计方差：

Weights  (5)

用等权拟合一个模型：

给出某些数据点的明确权：

使用 Around 值，以赋予数据点不同的权重：

找出用于考虑数据不确定性的权重：

在独立值和响应中使用 Around 值：

用 Around 值拟合一个以上变量的模型：

尝试使用 FixedPoint 算法来查找模型的权重：

降低 DampingFactor，增加 MaxIterations，以达到收敛：

WorkingPrecision  (1)

用 WorkingPrecision 在参数估计中得到更高的精度：

得到拟合函数：

在拟合后，化简属性计算中的精度：

应用  (6)

拟合一个线性模型的前 100 素数：

可视化显示拟合：

残差的系统趋向违背了独立正态误差的假设：

拟合多变量的线性模型：

按照数据点可视化检查残差：

绘制每个预期变量相应的残差：

绘制库克距离，诊断杠杆作用：

求出给出截断值上距离的坐标：

提取相关的数据点：

用 - 图形，检查正态误差的假设：

比较标准化残差和标准正态值：

比较 Studentized 残差：

模拟有连续变量和名义变量的某些数据：

分析数据的方差模型：

得到方差分析表：

按照处理方式将数据分组：

可视化显示分组数据和相关曲线：

用属性计算其它结果：

提取设计矩阵和残差：

计算White的异方差一致协方差估计：

假设同方差性比较协方差：

比较基于两个协方差估计的标准误差：

执行一个 Breusch Pagan 测试：

拟合一个模型：

拟合有相同预期值的模型的平方误差：

计算 Breusch Pagan 测试统计：

计算 值：

属性和关系  (9)

DesignMatrix 构建 LinearModelFit 使用的设计矩阵：

在缺省情况下，LinearModelFit 和 GeneralizedLinearModelFit 拟合等价模型：

假设正态分布误差，LinearModelFit 拟合线性模型：

假设正态分布误差，NonlinearModelFit 拟合非线性模型：

Fit 和 LinearModelFit 拟合等价模型：

LinearModelFit 允许提取拟合的其它信息：

拟合一个线性模型：

用设计矩阵和响应向量，执行相同拟合：

通过 LeastSquares 得到参数估计：

LinearModelFit 拟合线性模型：

FindFit 给出线性模型和非线性模型的参数估计：

LinearModelFit 使用 TimeSeries 的时间戳作为变量：

缩放时间戳，重新拟合：

拟合数值：

对于包含多个路径的 TemporalData，LinearModelFit 对各个路径分别进行拟合：

进行简单的线性模型拟合：

使用带有单个线性层的神经网络进行同样的拟合：

Wolfram Research (2008)，LinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LinearModelFit.html （更新于 2024 年）.

文本

Wolfram Research (2008)，LinearModelFit，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LinearModelFit.html （更新于 2024 年）.

CMS

Wolfram 语言. 2008. "LinearModelFit." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/LinearModelFit.html.

APA

Wolfram 语言. (2008). LinearModelFit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LinearModelFit.html 年

BibTeX

@misc{reference.wolfram_2024_linearmodelfit, author="Wolfram Research", title="{LinearModelFit}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/LinearModelFit.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_linearmodelfit, organization={Wolfram Research}, title={LinearModelFit}, year={2024}, url={https://reference.wolfram.com/language/ref/LinearModelFit.html}, note=[Accessed: 21-November-2024 ]}