- See Also
-
Related Guides
- Statistical Model Analysis
- Matrix-Based Minimization
- Tabular Modeling
- Statistical Data Analysis
- Tabular Processing Overview
- Numerical Data
- Life Sciences & Medicine: Data & Computation
- Scientific Data Analysis
- Scientific Models
- Time Series Processing
- Finite Mathematics
- Financial & Economic Data
- Supervised Machine Learning
- Financial Computation
- Tech Notes
-
- See Also
-
Related Guides
- Statistical Model Analysis
- Matrix-Based Minimization
- Tabular Modeling
- Statistical Data Analysis
- Tabular Processing Overview
- Numerical Data
- Life Sciences & Medicine: Data & Computation
- Scientific Data Analysis
- Scientific Models
- Time Series Processing
- Finite Mathematics
- Financial & Economic Data
- Supervised Machine Learning
- Financial Computation
- Tech Notes
LinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]
constructs a linear model of the form ![]() that fits the yi for successive xi values.
that fits the yi for successive xi values.
LinearModelFit[data,{f1,f2,…},{x1,x2,…}]
constructs a linear model where the fi depend on the variables xk.
LinearModelFit[{m,v}]
constructs a linear model from the design matrix m and response vector v.




LinearModelFit
LinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]
constructs a linear model of the form ![]() that fits the yi for successive xi values.
that fits the yi for successive xi values.
LinearModelFit[data,{f1,f2,…},{x1,x2,…}]
constructs a linear model where the fi depend on the variables xk.
LinearModelFit[{m,v}]
constructs a linear model from the design matrix m and response vector v.
Details and Options










- LinearModelFit attempts to model the input data using a linear combination of functions.
- LinearModelFit produces a linear model of the form
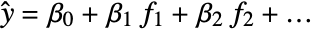 under the assumption that the original
under the assumption that the original 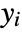 are independent normally distributed with mean
are independent normally distributed with mean 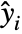 and common standard deviation.
and common standard deviation. - LinearModelFit returns a symbolic FittedModel object to represent the linear model it constructs.
- The value of the best-fit function from LinearModelFit at a particular point x1, … can be found from model[x1,…].
- Possible forms of data are:
-
{y1,y2,…} equivalent to the form {{1,y1},{2,y2},…} {{x11,x12,…,y1},…} a list of independent values xij and the responses yi {{x11,x12,…}y1,…} a list of rules between input values and response {{x11,x12,…},…}{y1,y2,…} a rule between a list of input values and responses {{x11,…,y1,…},…}n fit the n 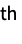 column of a matrix
column of a matrixTabular[…]name fit the column name in a tabular object - With multivariate data such as
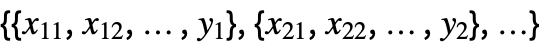 , the number of coordinates xi1, xi2, … should equal the number of variables xi.
, the number of coordinates xi1, xi2, … should equal the number of variables xi. - The data points can be approximate real numbers. Uncertainty can be specified using Around.
- Additionally, data can be specified using a design matrix without specifying functions and variables:
-
{m,v} a design matrix m and response vector v - In LinearModelFit[{m,v }], the design matrix m is formed from the values of basis functions fi at data points in the form {{f1,f2,…},{f1,f2,…},…}. The response vector v is the list of responses {y1,y2,…}.
- When a design matrix is used, the basis functions fi can be specified using the form LinearModelFit[{m,v},{f1,f2,…}].
- For a design matrix m and response vector v, the model is
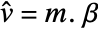 , where
, where 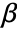 is the vector of parameters to be estimated.
is the vector of parameters to be estimated. - LinearModelFit takes the following options:
-
ConfidenceLevel 95/100 confidence level to use for parameters and predictions IncludeConstantBasis True whether to include a constant basis function LinearOffsetFunction None known offset in the linear predictor NominalVariables None variables considered as nominal or categorical VarianceEstimatorFunction Automatic function for estimating the error variance Weights Automatic weights for data elements WorkingPrecision Automatic precision used in internal computations - With the setting IncludeConstantBasis->False, a model of the form
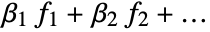 is fitted. The option IncludeConstantBasis is ignored if the design matrix is specified in the input.
is fitted. The option IncludeConstantBasis is ignored if the design matrix is specified in the input. - With the setting LinearOffsetFunction->h, a model of the form
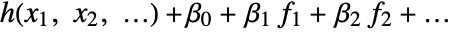 is fitted.
is fitted. - With ConfidenceLevel->p, probability-p confidence intervals are computed for parameter and prediction intervals.
- With the setting Weights->{w1,w2,…}, the error variance for yi is assumed proportional to
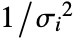 .
. - With the setting Weights->Automatic, the weights will be set to 1 if the data contains exact values. If the data contains Around values, the weights will be set to
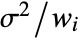 with
with 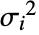 the total response variance.
the total response variance. - The total response variance
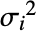 is a function of the initial response variance si2 and the independent values variance
is a function of the initial response variance si2 and the independent values variance 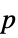 .
. - The
 are propagated through the model using AroundReplace and the resulting variance is added to response variance si2. The function FindRoot is used internally to find a self-consistent solution according to the Fasano and Vio method.
are propagated through the model using AroundReplace and the resulting variance is added to response variance si2. The function FindRoot is used internally to find a self-consistent solution according to the Fasano and Vio method. - With the setting VarianceEstimatorFunction->f, the variance is estimated by f[res,w], where res={y1-
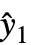 ,y2-
,y2-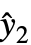 ,…} is the list of residuals and w={w1,w2,…} is the list of weights for the measurements yi.
,…} is the list of residuals and w={w1,w2,…} is the list of weights for the measurements yi. - Using VarianceEstimatorFunction->(1&) and Weights->{1/Δy12,1/Δy22,…}, Δyi is treated as the known uncertainty of measurement yi, and parameter standard errors are effectively computed only from the weights.
- The properties and diagnostics of the FittedModel can be obtained from model["property"].
- Properties related to data and the fitted function obtained using model["property"] include:
-
"BasisFunctions" list of basis functions "BestFit" fitted function "BestFitAround" fitted function and mean uncertainty "BestFitDataAround" fitted function and data uncertainty "BestFitParameters" parameter estimates "Data" the input data or design matrix and response vector "DesignMatrix" design matrix for the model "Function" best fit pure function "Response" response values in the input data "Weights" weights used to fit the data - Types of residuals include:
-
"FitResiduals" difference between actual and predicted responses "StandardizedResiduals" fit residuals divided by the standard error for each residual "StudentizedResiduals" fit residuals divided by single deletion error estimates - Properties related to the sum of squared errors include:
-
"ANOVA" analysis of variance data "CoefficientOfVariation" estimated standard deviation divided by the response mean "EstimatedVariance" estimate of the error variance "PartialSumOfSquares" changes in model sum of squares as nonconstant basis functions are removed "SequentialSumOfSquares" the model sum of squares partitioned componentwise - Properties and diagnostics for parameter estimates include:
-
"CorrelationMatrix" parameter correlation matrix "CovarianceMatrix" parameter covariance matrix "Eigenstructure" eigenstructure of the parameter correlation matrix "ParameterEstimates" table of fitted parameter information "VarianceInflationFactors" list of inflation factors for the estimated parameters - Properties related to influence measures include:
-
"BetaDifferences" DFBETAS measures of influence on parameter values "CatcherMatrix" catcher matrix "CookDistances" list of Cook distances "CovarianceRatios" COVRATIO measures of observation influence "DurbinWatsonD" Durbin–Watson 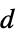 ‐statistic for autocorrelation
‐statistic for autocorrelation"FitDifferences" DFFITS measures of influence on predicted values "FVarianceRatios" FVARATIO measures of observation influence "HatDiagonal" diagonal elements of the hat matrix "SingleDeletionVariances" list of variance estimates with the 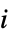
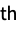 data point omitted
data point omitted - Properties of predicted values include:
-
"MeanPredictionBands" confidence bands for mean predictions "MeanPredictions" confidence intervals for the mean predictions "PredictedResponse" fitted values for the data "SinglePredictionBands" confidence bands based on single observations "SinglePredictions" confidence intervals for the predicted response of single observations - Properties that measure goodness of fit include:
-
"AdjustedRSquared" 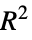 adjusted for the number of model parameters
adjusted for the number of model parameters"AIC" Akaike Information Criterion "AICc" finite sample corrected AIC "BIC" Bayesian Information Criterion "RSquared" coefficient of determination 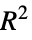
- The properties "BestFit", "BestFitAround", "BestFitDataAround", "SinglePredictionBands" and "MeanPredictionBands" can also be called as {"prop",x} or {"prop",{x1,x2,…}} to evaluate these properties at specific independent values.
- For the properties "RSquared" and "AdjustedRSquared", the computation of the total sum of squares is mean adjusted only when the constant basis is included.
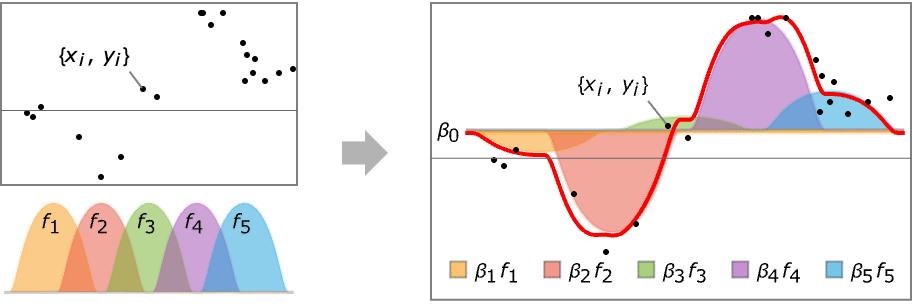
Data
Options
Properties
Examples
open all close allBasic Examples (1)
Scope (18)
Data (8)
Fit a model of one variable assuming increasing integer independent values:
Fit a model of more than one variable, assuming the response is the last one:
Specify a column as the response:
Fit a rule of input values and responses:
Fit a model with categorical predictor variables:
Fit a model given a design matrix and response vector:
Fit the model referring to the basis functions as x and y:
Fit a Tabular object by specifying the response column:
Model (3)
Properties (7)
Data & Fitted Functions (1)
Residuals (1)
Sums of Squares (1)
Parameter Estimation Diagnostics (1)
Influence Measures (1)
Fit some data containing extreme values to a linear model:
Use single deletion variances to check the impact on the error variance of removing each point:
Check Cook distances to identify highly influential points:
Use DFFITS values to assess the influence of each point on the fitted values:
Use DFBETAS values to assess the influence of each point on each estimated parameter:
Prediction Values (1)
Plot the predicted values against the observed values:
Obtain tabular results for the mean prediction confidence intervals:
Obtain tabular results for the single prediction confidence intervals:
Get the single prediction intervals from the table:
Extract 99% mean prediction bands:
Compute the 99% mean prediction bands at a specific location:
Generalizations & Extensions (1)
Options (11)
ConfidenceLevel (1)
The default gives 95% confidence intervals:
Set the level to 90% within FittedModel:
IncludeConstantBasis (1)
LinearOffsetFunction (1)
Fit data to a linear model with a known Sqrt[x] term:
NominalVariables (1)
VarianceEstimatorFunction (1)
Weights (5)
Fit a model using equal weights:
Give explicit weights for the data points:
Use Around values to give different weights to data points:
Find the weights that were used to account for the uncertainty in the data:
Use Around values in both the independent values and responses:
Fit a model of more than one variable with Around values:
Try the FixedPoint algorithm to find the weights for the model:
Reduce the damping factor and increase the MaxIterations to reach convergence:
WorkingPrecision (1)
Use WorkingPrecision to get higher precision in parameter estimates:
Reduce the precision in property computations after the fitting:
Applications (6)
Fit the first 100 primes to a linear model:
The systematic trend in the residuals violates the assumption of independent normal errors:
Fit a linear model of multiple variables:
Visually inspect the residuals by data point:
Plot the residuals against each predictor variable:
Plot Cook's distances to diagnose leverage:
Find the positions of distances above a given cutoff value:
Extract the associated data points:
Use ![]() -
-![]() plots to check the assumption of normal errors:
plots to check the assumption of normal errors:
Compare standardized residuals to standard normal values:
Do the comparison with Studentized residuals:
Simulate some data with a continuous and a nominal variable:
Fit an analysis of covariance model to the data:
Obtain an analysis of variance table for the model:
Visualize the grouped data and associated curves:
Use properties to compute additional results:
Extract the design matrix and residuals:
Compute White's heteroskedasticity-consistent covariance estimate:
Compare with the covariance assuming homoskedasticity:
Compare standard errors based on the two covariance estimates:
Fit the squared errors to a model with the same predictors:
Properties & Relations (10)
DesignMatrix constructs the design matrix used by LinearModelFit:
By default, LinearModelFit and GeneralizedLinearModelFit fit equivalent models:
LinearModelFit fits linear models assuming normally distributed errors:
NonlinearModelFit fits nonlinear models assuming normally distributed errors:
Fit and LinearModelFit fit equivalent models:
LinearModelFit allows for extraction of additional information about the fitting:
Perform the same fitting using a design matrix and response vector:
Obtain the parameter estimates via LeastSquares:
LinearModelFit fits linear models:
FindFit gives parameter estimates for linear and nonlinear models:
LinearModelFit will use the time stamps of a TimeSeries as variables:
Rescale the time stamps and fit again:
LinearModelFit acts pathwise on a multipath TemporalData:
Do the same fit using a neural net with a single linear layer:
Compute the AIC from first principles:
Compute the ![]() from first principles:
from first principles:
If the model does not include a constant basis, the denominator is not mean adjusted:
Tech Notes
Related Guides
-
▪
- Statistical Model Analysis ▪
- Matrix-Based Minimization ▪
- Tabular Modeling ▪
- Statistical Data Analysis ▪
- Tabular Processing Overview ▪
- Numerical Data ▪
- Life Sciences & Medicine: Data & Computation ▪
- Scientific Data Analysis ▪
- Scientific Models ▪
- Time Series Processing ▪
- Finite Mathematics ▪
- Financial & Economic Data ▪
- Supervised Machine Learning ▪
- Financial Computation
History
Introduced in 2008 (7.0) | Updated in 2023 (13.3) ▪ 2024 (14.1) ▪ 2025 (14.2) ▪ 2025 (14.3)
Text
Wolfram Research (2008), LinearModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/LinearModelFit.html (updated 2025).
CMS
Wolfram Language. 2008. "LinearModelFit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/LinearModelFit.html.
APA
Wolfram Language. (2008). LinearModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearModelFit.html
BibTeX
@misc{reference.wolfram_2025_linearmodelfit, author="Wolfram Research", title="{LinearModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/LinearModelFit.html}", note=[Accessed: 17-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_linearmodelfit, organization={Wolfram Research}, title={LinearModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/LinearModelFit.html}, note=[Accessed: 17-December-2025]}