MeanDeviation
MeanDeviation[data]
gives the mean absolute deviation from the mean of the elements in data.
Details


- MeanDeviation is also known as MAD.
- MeanDeviation is a measure of dispersion.
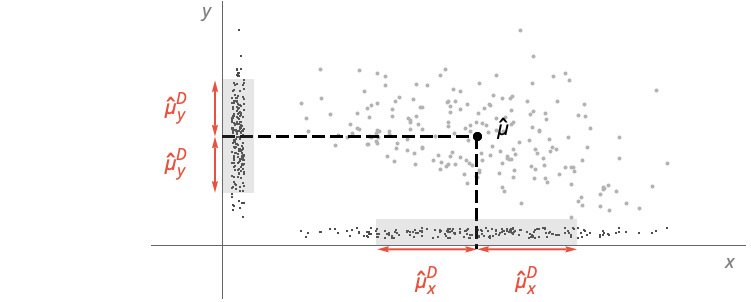
- For VectorQ data
 , the mean deviation
, the mean deviation 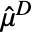 is given by
is given by 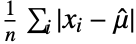 , where
, where 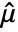 is the mean of data.
is the mean of data. - For MatrixQ data, the mean deviation is computed for each column vector with MeanDeviation[{{x1,y1,…},{x2,y2,…},…}] equivalent to {MeanDeviation[{x1,x2,…}],MeanDeviation[{y1,y2,…}],…}. »
- For ArrayQ data, the mean deviation is equivalent to ArrayReduce[MeanDeviation,data,1]. »
- MeanDeviation handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times »
Examples
open allclose allBasic Examples (4)
MeanDeviation of a list of numbers:
MeanDeviation of symbolic data:
MeanDeviation of the columns of a matrix:
MeanDeviation of a list of dates:
Scope (18)
Basic Uses (6)
Exact input yields exact output:
Approximate input yields approximate output:
Find the mean deviation of WeightedData:
Find the mean deviation of EventData:
Find the mean deviation for TimeSeries:
Array Data (5)
MeanDeviation for a matrix works columnwise:
MeanDeviation for a tensor works across the first index: »
When the input is an Association, MeanDeviation works on its values:
SparseArray data can be used just like dense arrays:
Find mean deviation of a QuantityArray:
Image and Audio Data (2)
Channelwise mean deviation value of an RGB image:
Mean deviation value of a grayscale image:
On audio objects, MeanDeviation works channelwise:
Applications (3)
Properties & Relations (4)
MeanDeviation is the Mean of absolute deviations from the Mean:
MeanDeviation is equivalent to the 1‐norm of the deviations divided by the Length:
For large uniform datasets, MeanDeviation and MedianDeviation are nearly the same:
MeanDeviation as a scaled ManhattanDistance from the Mean:
Neat Examples (1)
Ratio of MeanDeviation to MedianDeviation for increasing sample size:
Text
Wolfram Research (2007), MeanDeviation, Wolfram Language function, https://reference.wolfram.com/language/ref/MeanDeviation.html (updated 2024).
CMS
Wolfram Language. 2007. "MeanDeviation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/MeanDeviation.html.
APA
Wolfram Language. (2007). MeanDeviation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanDeviation.html