MixtureDistribution
MixtureDistribution[{w1,…,wn},{dist1,…,distn}]
それぞれが重み wiを持つ成分分布 distiの累積分布関数の和として累積分布関数が与えられる混合分布を表す.
詳細
- 値
 の累積分布関数は,
の累積分布関数は,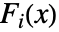 が distiの累積分布関数である
が distiの累積分布関数である 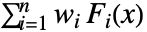 に比例する.
に比例する. - 分布 distiはすべて連続的かすべて離散的かのどちらかでなければならない.また,次元がすべて等しくなければならない.
- 重み wiは任意の非負の実数でよい.
- MixtureDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
例題
すべて開くすべて閉じるスコープ (30)
基本的な用法 (10)
パラメトリック分布 (5)
ノンパラメトリック分布 (3)
SmoothKernelDistributionとの混合分布を定義する:
EmpiricalDistributionとの混合分布を定義する:
HistogramDistributionとの混合分布を定義する:
派生分布 (10)
MixtureDistributionで与えられる成分の混合分布を定義する:
最大値と最小値のOrderDistributionの混合分布を求める:
TruncatedDistributionの混合分布を求める:
ProductDistributionの混合分布の確率密度関数を求める:
TransformedDistributionの混合分布を定義する:
MarginalDistributionの混合分布を定義する:
CensoredDistributionとの混合分布を定義する:
ParameterMixtureDistributionとの混合分布:
CopulaDistributionとの混合分布を定義する:
互換的なQuantityDistributionの混合分布を評価するとQuantityDistributionになる:
PDFをプロットする:
アプリケーション (7)
NProbabilityを使ってこれを関数としてまとめる:
アメリカ合衆国の女性の身長は正規分布に従っており,平均64インチ,標準偏差は2インチである.男性の身長も正規分布に従っており,平均70インチ,標準偏差は2インチである.人口の男女比が1.1対1の場合,総人口の身長は次のような二峰性分布になる:
人口100人の町の典型的な身長分布のシミュレーションを行う:
あるバイナリ伝送ではコード0で![]() ボルトの信号を,コード1で
ボルトの信号を,コード1で ![]() ボルトの信号を送る.1は確率
ボルトの信号を送る.1は確率 ![]() で送られるが信号はホワイトノイズで破損するとして,受信された信号の確率密度関数を求める:
で送られるが信号はホワイトノイズで破損するとして,受信された信号の確率密度関数を求める:
p=0.4で v=1の受信機での伝送のシミュレーションを行う:
2つの信号を区別するためには電位差がより大きくなければならない:
MixtureDistributionを使って多峰モデルを作成することができる:
選択した年代における合衆国の地震のマグニチュードには2つのモードがある:
これから起る30の地震のマグニチュードのシミュレーションを行う:
中型車の市街地と高速道路での平均走行可能距離は二変量正規分布に従う:
運転の65%が市街地で行われると仮定すると走行可能距離はMixtureDistributionに従う:
ガウス混合モデルは画像分割のためによく使われる.画像は画素の配列として表される.画素は強度(あるいは色)を示すスカラー(あるいはベクトル)である:
Histogramを使って画素値の分布を可視化する:
EstimatedDistributionを使って画素値を3要素のガウス混合にフィットする:
特性と関係 (8)
重み w の混合分布は重み w/Total[w]のものと等価である:
混合分布の確率密度関数はその成分の確率密度関数の凸結合である:
混合分布の累積分布関数はその成分の累積分布関数の凸結合である:
有限個の値を仮定すると,離散重みを持つParameterMixtureDistributionは混合分布で表すことができる:
可算個の値を仮定すると,離散重みを持つParameterMixtureDistributionは混合分布で近似することができる:
連続的な重みを持つParameterMixtureDistributionを混合分布で近似する:
KernelMixtureDistributionはデータから派生したMixtureDistributionである:
テキスト
Wolfram Research (2010), MixtureDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MixtureDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "MixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MixtureDistribution.html.
APA
Wolfram Language. (2010). MixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MixtureDistribution.html