RSolveValue

RSolveValue[eqn,expr,n]

给出 expr 的值，其值由自变量为 n 的常差分方程 eqn 的一个符号解决定.

RSolveValue[{eqn1,eqn2,…},expr,…]

使用一组差分方程的符号解.

RSolveValue[eqn,expr,{n1,n2,…}]

使用部分递推方程 eqn 的解.

更多信息和选项

  • RSolveValue[eqn,a,n] 给出 a 为纯函数的解.
  • 方程可涉及形为 a[n+λ] 的对象，其中 λ 是常量，或推广为形式为 a[ψ[n]]、a[ψ[ψ[n]]、a[ψ[…[ψ[n]]…]] 的对象，ψ 可有以下形式：
  • n+λ算术差分方程
    μ n几何或 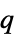-差分方程
    μ n+λ算术-几何函数差分方程
    μ nα几何-幂函数差分方程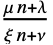
    线性分数函数差分方程
  • 可以给出像 a[0]==val 这样的方程来指定结束条件.
  • 如果没有指定足够多的结束条件，RSolveValue 将使用引入未定常数的通解.
  • 可通过指定 a∈Vectors[p] 或 a∈Matrices[{m,p}] 来表明自变量 a 的值是向量或矩阵. » »
  • 用整数对由 RSolveValue 引入的常数进行索引. 选项 GeneratedParameters 指定应用于每个索引的函数. 默认为GeneratedParameters->C，它会生成常数 C[1]、C[2] ….
  • GeneratedParameters->(Module[{C},C]&) 保证积分常数是唯一的，甚至在不同的 RSolveValue 调用之间.
  • 对于部分递推方程， RSolveValue 将生成任意函数 C[n][…].
  • 由 RSolveValue 给出的解在某些时候包括不能直接被 Sum 计算的和. 可在这样的和中使用有局部名称的虚变量.
  • RSolveValue[eqn,a[Infinity],n] 给出解 a 在 Infinity 处的极限值.
  • RSolveValue 能处理常差分方程和 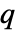-差分方程.
  • RSolveValue 能处理差分-代数方程以及常差分方程.
  • RSolveValue 可以求解常系数的任意阶线性递推方程. 它还可以求解许多非常数系数的最大阶数为二的线性方程，以及许多非线性方程.
  • RSolveValue[u[t]sys,resp,t] 可用于解离散时间模型，其中 sys 可以是 TransferFunctionModel 或 StateSpaceModel，响应函数 resp 可为以下形式： »
  • "StateResponse"sys 对输入 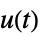的状态响应
    "OutputResponse"sys 对输入 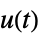的输出响应

范例

打开所有单元关闭所有单元

基本范例  (4)

解一个差分方程：

包含一个边界条件：

得到一个a 的"纯函数"解：

对这个解绘图：

解一个函数方程：

获得在一个点的解的值：

值的列表：

范围  (54)

基本用途  (9)

计算一阶差分方程的通解：

通过附加一个初始条件获得一个特殊解：

绘制一阶差分方程的解：

生成一个值的表：

通过第二个参数用 a 来验证差分方程的解：

获得一个高阶差分方程的通解：

特殊解：

解一组差分方程：

对它们的解绘图：

验证解：

计算解在某个点的值：

计算解在 Infinity 处的极限值：

解一个偏差分方程：

获得一个特殊解：

绘制得到的解：

在通解里面对任意常数用不同名：

线性差分方程  (7)

几何方程：

有变系数的一阶方程：

一个三阶的常系数方程：

初始值条件：

对得到的解绘图：

二阶非齐次方程：

依照初等函数的二阶变系数方程：

柯西-欧拉方程：

通常来说，解的表达需要特殊函数：

具有恒定系数的高阶非均质方程：

非线性差分方程  (5)

可解的逻辑斯谛方程：

Riccati 方程：

依照三角和双曲函数的解：

高阶方程：

非线性卷积方程：

差分方程组  (8)

常系数线性方程组：

有边界条件：

绘制解：

线性分数方程组：

对角方程组：

有多项式解的变系数线性方程组：

线性常系数差分-代数方程组：

一个 index-2 方程组：

用向量变量求解线性方程组：

用矩阵变量变量求解线性方程组：

求解具有恒定系数的非均质线性常微分方程组：

部分差分方程  (3)

有常系数的一阶线性部分差分方程：

用函数 Sin[2k] 替代自由函数 C[1]：

绘制所得的解：

2、3、4 阶常系数线性方程：

非齐次：

变系数线性方程：

Q–差分方程  (6)

一阶常系数 -差分方程：

同一个方程的另外一种表达方式：

初始值：

二阶方程：

三阶：

非齐次：

对 用一个数值：

对得到的解绘图：

线性变系数方程：

非线性方程：

Riccati 方程：

-差分方程的线性常系数系统：

泛函差分方程  (4)

找到算术差分方程的通解：

验证解：

解算术-几何差分方程的初始值问题：

对得到的解绘图：

解一个线性分数差分方程：

生成一个解的值的表：

解一个几何幂差分方程：

验证解：

递归数列的极限  (5)

计算线性递归数列的极限值：

图示数列收敛至极限值：

计算线非性递归数列的极限值：

图示数列收敛至极限值：

计算三角递归数列的极限值：

图示数列收敛至极限值：

计算二阶递归数列的极限值：

图示数列收敛至极限值：

对满足差分方程的斐波纳契序列计算相邻项比值 (f[n+1]/f[n]) 的极限：

求解差分方程，计算比值：

用 DiscreteLimit 计算比值的极限：

图示数列收敛至极限值：

或者使用 RSolveValue 的 DiscreteLimit 计算极限：

系统模型  (7)

计算离散时间 StateSpaceModel 对正弦输入信号的 OutputResponse 和 StateResponse：

传递函数模型对正弦输入的输出响应：

非零初始条件下状态空间模型的响应：

单输入系统对单位阶跃输入的状态响应：

绘制八个步阶的响应：

通用离散时间系统的状态响应：

对单位阶跃序列的输出响应：

离散时间系统对时间依赖的输入的输出响应：

τ=0.1 的响应：

推广和延伸  (2)

得到解的平方的一个表达式：

没有边界条件给出两个产生参数：

一个边界条件：

两个边界条件：

选项  (1)

GeneratedParameters  (1)

用不同命名的常数：

用下标常数：

应用  (13)

这是模拟当只对本金 p 付了利息 r 时，第 n 年的数额 a[n] :

这是对当前数额 a[n] 所付的利息，即复利：

这里 a[n] 表示有 n 个圆盘的汉诺塔问题所需要移动的次数：

这里 a[n] 是用 2×1 的瓷砖铺一个 n×3 的空间的方法数：

折半搜索问题中需做比较的次数：

快速傅里叶变换中算术运算操作的次数：

嵌套根式 满足非线性差分方程：

计算嵌套根式的精确值：

图示数列收敛至精确值：

积分 满足差分方程：

积分 满足差分方程：

的级数系数的差分方程:

一个 n×n，对角线 为c，a，b 的三对角矩阵的行列式满足：

模拟在 n 维的单位球体的表面积 s[n]：

在 n 维的单位球体的体积：

对 应用牛顿法，或计算：

对 应用前向欧拉方法，得到：

解这个描述 Karatsuba 乘算法复杂度的差分方程：

比较教科书乘算法的复杂度：

对于较大的 n，计算线性递归数列的第 n 项：

属性和关系  (10)

RSolveValue 返回解的一个表达式：

RSolve 返回一个解的规则：

解满足它们的差分和边界方程：

对应于 Sum 的差分方程：

对应于 Product 的差分方程：

RSolveValue 找到该差分方程的一个符号解：

RecurrenceTable 生成同样一个问题的子程序解：

FindLinearRecurrence 找到一个列表的最小线性递推：

RSolveValue 找到满足递推的序列：:

LinearRecurrence 产生线性递归数列的第 n 项：

用 RSolveValue 获得同样的结果：

用 RecurrenceFilter 过滤一个信号：

用 RSolveValue 解相对应的差分方程：

预测基于 ARProcess 的时间序列的下一个值：

用 RSolveValue 得到同样的结果：

用 RFixedPoints 求由两个递归方程组成的方程组的不动点：

用 RStabilityConditions 分析不动点的稳定性：

用不动点作为初始条件，求解方程组：

针对给定的初始条件求解方程组：

绘制解：

可能存在的问题  (4)

大写的 和大写的 不能被用作自变量：

用小写的 或小写的 进行替换：

作为一个序列，该差分方程的解是唯一的：

作为一个函数，它只在上至周期 1 的函数的范围是唯一的：

RSolveValue 只返回单个分支如果解有多个分支：

用 RSolve 得到所有解的分支：

验证方程涉及到有下标的变量时的解：

巧妙范例  (1)

计算一个函数的第 n 次迭代或组成:

Wolfram Research (2014)，RSolveValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RSolveValue.html （更新于 2024 年）.

文本

Wolfram Research (2014)，RSolveValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RSolveValue.html （更新于 2024 年）.

CMS

Wolfram 语言. 2014. "RSolveValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/RSolveValue.html.

APA

Wolfram 语言. (2014). RSolveValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RSolveValue.html 年

BibTeX

@misc{reference.wolfram_2024_rsolvevalue, author="Wolfram Research", title="{RSolveValue}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RSolveValue.html}", note=[Accessed: 07-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rsolvevalue, organization={Wolfram Research}, title={RSolveValue}, year={2024}, url={https://reference.wolfram.com/language/ref/RSolveValue.html}, note=[Accessed: 07-November-2024 ]}