RegionCentroid

RegionCentroid[reg]

gives the centroid of the region reg.

Details and Options

  • RegionCentroid is also known as center of mass, center of gravity, or barycenter.
  • The centroid is effectively given by Integrate[{x1,…,xn},{x1,…,xn}∈reg]/RegionMeasure[reg].
  • The centroid is in the region when the region is convex. Otherwise it is typically not in the region.
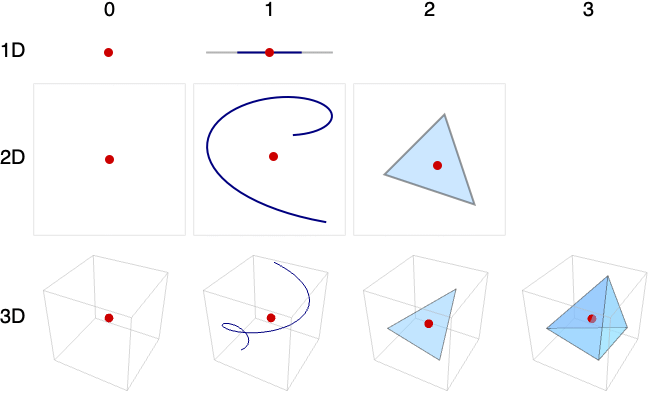
  • Examples of cases where rows correspond to embedding dimension and columns to geometric dimension:
  • If the region reg consists of a finite number of points, the RegionCentroid gives the mean.
  • A region with infinite RegionMeasure has no RegionCentroid and returns a point with Indeterminate coordinates.
  • RegionCentroid takes an Assumptions option that can be used to specify assumptions on parameters.
  • RegionCentroid can be used with symbolic regions in GeometricScene.

Examples

open allclose all

Basic Examples  (2)

Find the centroid of a region:

The centroid of a Polygon:

Scope  (21)

Special Regions  (10)

The centroid for Point corresponds to the mean of the coordinates:

Points can be used in any number of dimensions:

Line:

Lines can be used in any number of dimensions:

Rectangle can be used in 2D:

Cuboid can be used in any number of dimensions:

A 4D Cuboid:

A Simplex can correspond to a point, line, or triangle in 2D:

Simplices can be used in any number of dimensions:

The centroid of a standard unit Simplex in dimension :

The centroid of a Polygon may lie outside the region:

In 3D:

Disk can be used in 2D:

Ball can be used in any dimension:

In 4D:

Disk as an ellipse can be used in 2D:

Ellipsoid can be used in any dimension:

Circle can be used in 2D:

As an ellipse:

Cylinder can be used in 3D:

Cone can be used in 3D:

Formula Regions  (2)

The centroid of a disk represented as an ImplicitRegion:

The centroid of a cylinder:

The centroid of a disk represented as a ParametricRegion:

Using a rational parameterization of the disk:

The centroid of a cylinder:

Mesh Regions  (2)

The centroid of a MeshRegion:

A 1D mesh embedded in 2D:

In 3D:

The centroid of a BoundaryMeshRegion:

In 3D:

Derived Regions  (5)

The centroid of a RegionIntersection:

The centroid of a TransformedRegion:

The centroid of a RegionBoundary:

General Boolean combination :

Inverse transformed region :

Geographic Regions  (2)

The centroid of a polygon with GeoPosition:

The centroid of a polygon with GeoGridPosition:

Applications  (5)

Find the center of mass for a mesh region:

Compute the center of mass of a region with density given by and compare to the centroid:

Visualize it:

The center of mass is shifted because the density is highest in the lower-left:

Find a perpendicular bisector of a triangle:

Visualize circumcenter and bisectors in red:

Compute a centroidal Voronoi diagram from a random set of points:

Define a function that computes the centroid of each Voronoi region in a Voronoi mesh:

Recursively apply VoronoiMesh to the centroids of the precursive Voronoi regions:

Visualize the Voronoi mesh and centroids at each iteration:

The generating point (black) of each Voronoi region converges toward the region's centroid (red):

Estimate the centroid of a region by taking the Mean of a random sampling of points in the region:

Properties & Relations  (3)

RegionCentroid is not necessarily in the region if the region is not convex:

RegionCentroid is equivalent to Integrate[p,p∈ℛ]/m with m=RegionMeasure[ℛ]:

The centroid for is given by when disjoint:

Possible Issues  (1)

RegionCentroid returns a point with Indeterminate coordinates for a region with infinite RegionMeasure:

Wolfram Research (2014), RegionCentroid, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionCentroid.html.

Text

Wolfram Research (2014), RegionCentroid, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionCentroid.html.

CMS

Wolfram Language. 2014. "RegionCentroid." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionCentroid.html.

APA

Wolfram Language. (2014). RegionCentroid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionCentroid.html

BibTeX

@misc{reference.wolfram_2024_regioncentroid, author="Wolfram Research", title="{RegionCentroid}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionCentroid.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regioncentroid, organization={Wolfram Research}, title={RegionCentroid}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionCentroid.html}, note=[Accessed: 21-November-2024 ]}