RegionCentroid

RegionCentroid[reg]

領域 reg の重心を与える．

詳細とオプション

  • RegionCentroidは，質量中心，力学重心，重心等としても知られている．
  • 重心は，事実上，Integrate[{x1,…,xn},{x1,…,xn}∈reg]/RegionMeasure[reg]で与えられる．
  • 領域が凸面のとき，重心は領域内にある．それ以外の場合は，通常，重心は領域内にはない．
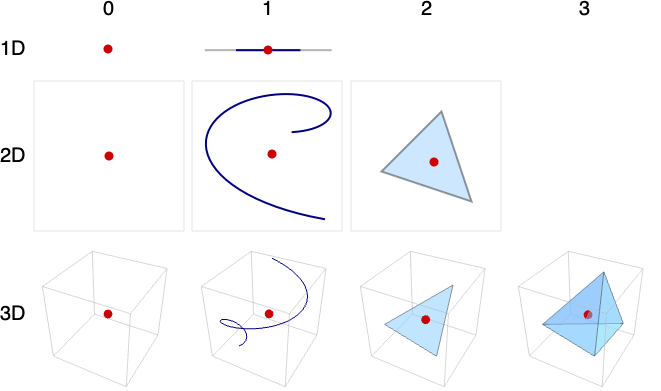
  • 行が埋込み次元，列が幾何学次元に対応する，いくつかの例．
  • 領域 reg が有限個の点からなっている場合，RegionCentroidは平均を与える．
  • 無限のRegionMeasureからなる領域にはRegionCentroidはなく，点がIndeterminate座標で返される．
  • RegionCentroidは，パラメータに関する仮定を指定するために使うことができるAssumptionsオプションを取る．
  • RegionCentroidは，GeometricSceneの記号領域と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

領域の重心を求める：

Polygonの重心：

スコープ  (21)

特別領域  (10)

Pointについての重心は座標の平均に相当する：

点は任意の次元に使うことができる：

Line：

線は任意数の次元に使うことができる：

Rectangleは2Dで使うことができる：

Cuboidは任意数の次元で使うことができる：

4DのCuboid：

Simplexは，2Dの点，線，三角形のいずれかに合致することができる：

単体は任意数の次元で使うことができる：

次元の標準的な単位Simplexの重心：

Polygonの重心は領域の外側にあることがある：

3Dで：

Diskは2Dで使うことができる：

Ballは任意の次元で使うことができる：

4Dで：

楕円としてのDiskは2Dで使うことができる：

Ellipsoidは任意の次元で使うことができる：

Circleは2Dで使うことができる：

楕円として：

Cylinderは3Dで使うことができる：

Coneは3Dで使うことができる：

数式定義領域  (2)

ImplicitRegionとして表された円板の重心：

円柱の重心：

ParametricRegionとして表された円板の重心：

円板の有理パラメータ化を使う：

円柱の重心：

メッシュ領域  (2)

MeshRegionの重心：

2Dに埋め込まれた1Dメッシュ：

3Dに：

BoundaryMeshRegionの重心：

3Dでの：

派生領域  (5)

RegionIntersectionの重心：

TransformedRegionの重心：

RegionBoundaryの重心：

一般的なブール値の組合せ：

逆変換された領域 ：

地理的領域  (2)

GeoPositionを使った多角形の重心：

GeoGridPositionを使った多角形の重心：

アプリケーション  (5)

メッシュ領域の質量中心を求める：

で与えられる，密度を持つ領域の質量の中心を計算し，重心と比べる：

これを可視化する：

密度が左下で最も高くなるので，質量の中心がシフトする：

三角形の垂直二等分線を求める：

外心と垂直二等分線を赤で可視化する：

点のランダムな集合から，重心ボロノイ図を計算する：

ボロノイメッシュ中の各ボロノイ領域の重心を計算する関数を定義する：

先行するボロノイ領域の重心にVoronoiMeshを反復的に適用する：

各反復におけるボロノイメッシュと重心を可視化する：

各ボロノイ領域の生成点（黒）は領域の重心（赤）に収束する：

領域内の点を無作為抽出したサンプルのMeanを取ることで，領域の重心を推測する：

特性と関係  (3)

RegionCentroidは，領域が凸状ではない場合は，必ずしも領域内にある訳ではない：

RegionCentroidは，m=RegionMeasure[ℛ]であるIntegrate[p,p∈ℛ]/m に等しい：

についての重心は，互いに素な場合は，で与えられる：

考えられる問題  (1)

RegionCentroidは，無限RegionMeasureの領域については，Indeterminate座標の点を返す：

Wolfram Research (2014), RegionCentroid, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionCentroid.html.

テキスト

Wolfram Research (2014), RegionCentroid, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionCentroid.html.

CMS

Wolfram Language. 2014. "RegionCentroid." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionCentroid.html.

APA

Wolfram Language. (2014). RegionCentroid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionCentroid.html

BibTeX

@misc{reference.wolfram_2024_regioncentroid, author="Wolfram Research", title="{RegionCentroid}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionCentroid.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regioncentroid, organization={Wolfram Research}, title={RegionCentroid}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionCentroid.html}, note=[Accessed: 21-November-2024 ]}