RegionCentroid
RegionCentroid
RegionCentroid[reg]
给出区域 reg 的几何中心.
更多信息和选项
- RegionCentroid 又被称为质量中心，引力中心，或重心.
- 几何中心由 Integrate[{x1,…,xn},{x1,…,xn}∈reg]/RegionMeasure[reg] 有效给出.
- 当区域是凸的，几何中心在区域内. 否则它一般不在区域内.
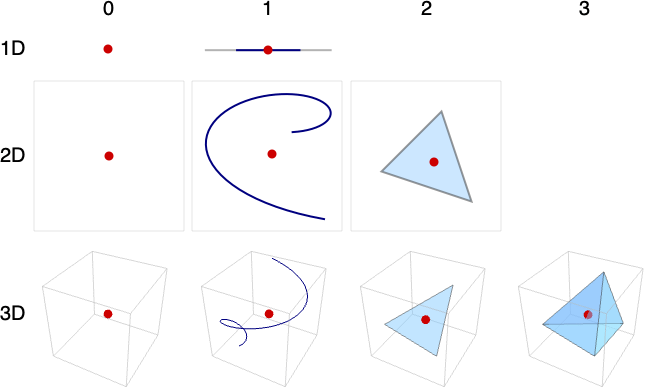
- 范例（行对应于嵌入维度和列对应于几何维度）：
- 如果区域 reg 由有限个点组成，RegionCentroid 将给出平均值.
- 有无限 RegionMeasure 的区域没有 RegionCentroid，将返回一个有 Indeterminate 坐标的点.
- RegionCentroid 接受一个可用来指定参数的假定的选项 Assumptions .
- RegionCentroid 可用于 GeometricScene 中的符号区域.
范例
打开所有单元 关闭所有单元基本范例 (2)
RegionCentroid[Disk[{x, y}, r]]RegionCentroid[Rectangle[{a, b}, {c, d}]]Polygon 的几何中心：
ℛ = Polygon[{{0, 0}, {1, 0}, {1.5, 0.5}, {1, 1}, {0, 1}, {-0.5, 0.5}}];RegionCentroid[ℛ]Graphics[{LightBlue, ℛ, Red, Point[RegionCentroid[ℛ]]}]范围 (25)
特定区域 (10)
Point 的几何中心对应于坐标的平均值：
ℛ = Point[Tuples[Range[5], 2]];
Region[ℛ]RegionCentroid[ℛ]RegionCentroid[Point[Tuples[Range[5], 4]]]Line：
ℛ = Line[{{0, 0}, {1, 1}, {1, 0}}];
Graphics[{ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]RegionCentroid[Line[{{0}, {1}}]]RegionCentroid[Line[{{0, 0, 0}, {1, 1, 1}}]]Rectangle 可用在二维：
RegionCentroid[Rectangle[{Subscript[l, x], Subscript[l, y]}, {Subscript[u, x], Subscript[u, y]}]]ℛ = Rectangle[{0, 1}, {3, 3}];
Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Cuboid 可用在任意数目的维度：
RegionCentroid[Cuboid[{Subscript[l, x], Subscript[l, y], Subscript[l, z]}, {Subscript[u, x], Subscript[u, y], Subscript[u, z]}]]ℛ = Cuboid[{1, 2, 3}, {5, 5, 5}];
Graphics3D[{{Opacity[0.5], ℛ}, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]四维 Cuboid：
RegionCentroid[Cuboid[{Subscript[l, x], Subscript[l, y], Subscript[l, z], Subscript[l, w]}, {Subscript[u, x], Subscript[u, y], Subscript[u, z], Subscript[u, w]}]]Simplex 可对应于点，线或二维三角形：
ℛ = {Simplex[{{0, 0}}], Simplex[{{0, 0}, {1, 1}}], Simplex[{{0, 0}, {1, 0}, {0, 1}}]};Table[Framed@Graphics[{Lighter[Blue, 0.5], s, Red, Point[RegionCentroid[s]]}, ImageSize -> 50], {s, ℛ}]RegionCentroid /@ ℛRegionCentroid[Simplex[{{0}, {1}}]]RegionCentroid[Simplex[{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}}]]在 
维的标准单位 Simplex 的几何中心：
Table[RegionCentroid[Simplex[n]], {n, 1, 5}]Polygon 的几何中心可能会在区域外：
ℛ = Polygon[{{0, 0}, {3, -1}, {1, 0}, {3, 1}}];
Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]ℛ = Polygon[{{0, 0, 0}, {(5/3), (2/3), -(4/3)}, {(8/15), (8/15), -(4/15)}, {1, 2, 0}}];
Graphics3D[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Disk 可被用在二维：
RegionCentroid[Disk[{Subscript[c, x], Subscript[c, y]}, r]]ℛ = Disk[{2, 3}, 2];
Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Ball 可被用在任何维度：
RegionCentroid[Ball[{Subscript[c, x], Subscript[c, y], Subscript[c, z]}, r]]ℛ = Ball[{1, 2, 3}, 4];
Graphics3D[{{Opacity[0.5], ℛ}, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]RegionCentroid[Ball[{Subscript[c, x], Subscript[c, y], Subscript[c, z], Subscript[c, w]}, r]]作为椭圆的 Disk 可被用在二维：
RegionCentroid[Disk[{Subscript[c, x], Subscript[c, y]}, {Subscript[r, x], Subscript[r, y]}]]ℛ = Disk[{0, 0}, {3, 2}];
Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Ellipsoid 可用在任何维度：
RegionCentroid[Ellipsoid[{Subscript[c, x], Subscript[c, y], Subscript[c, z], Subscript[c, w]}, {Subscript[r, x], Subscript[r, y], Subscript[r, z], Subscript[r, w]}]]ℛ = Ellipsoid[{0, 0, 0}, {3, 2, 1}];
Graphics3D[{{Opacity[0.5], ℛ}, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Circle 可用在二维：
RegionCentroid[Circle[{Subscript[c, x], Subscript[c, y]}, r]]ℛ = Circle[{0, 0}, 1];
Graphics[{ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]RegionCentroid[Circle[{Subscript[c, x], Subscript[c, y]}, {Subscript[r, x], Subscript[r, y]}]]ℛ = Circle[{0, 0}, {3, 2}];
Graphics[{ℛ, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Cylinder 可被用在三维：
RegionCentroid[Cylinder[{{Subscript[x, 1], Subscript[y, 1], Subscript[z, 1]}, {Subscript[x, 2], Subscript[y, 2], Subscript[z, 2]}}, r]]ℛ = Cylinder[{{0, 0, 0}, {0, 0, 2}}, 1];
Graphics3D[{{Opacity[0.5], ℛ}, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]Cone 可被用在三维：
RegionCentroid[Cone[{{Subscript[x, 1], Subscript[y, 1], Subscript[z, 1]}, {Subscript[x, 2], Subscript[y, 2], Subscript[z, 2]}}, r]]ℛ = Cone[{{0, 0, 0}, {0, 0, 2}}, 1];
Graphics3D[{{Opacity[0.5], ℛ}, Red, Point[RegionCentroid[ℛ]]}]RegionCentroid[ℛ]公式区域 (2)
圆盘的几何中心被表示成 ImplicitRegion：
RegionCentroid[ImplicitRegion[x^2 + y^2 ≤ 1, {x, y}]]RegionCentroid[ImplicitRegion[x^2 + y^2 ≤ 1, {x, y, {z, 0, 2}}]]圆盘的几何中心被表示成 ParametricRegion：
RegionCentroid[ParametricRegion[{r Cos[θ], r Sin[θ]}, {{r, 0, 1}, {θ, 0, 2π}}]]RegionCentroid[ParametricRegion[{r(1 - t^2/1 + t^2), r(2t/1 + t^2)}, {t, {r, 0, 1}}]]RegionCentroid[ParametricRegion[{r Cos[θ], r Sin[θ], z}, {{r, 0, 1}, {θ, 0, 2π}, {z, 0, 2}}]]网格区域 (2)
MeshRegion 的几何中心：
ℛ = DelaunayMesh[RandomReal[1, {10, 2}]];c = RegionCentroid[ℛ]Show[ℛ, Graphics[{Red, Point[c]}]]ℛ = MeshRegion[{{0, 0}, {1, 0}, {2, -1}, {2, 1}}, {Line[{{1, 2, 3, 4, 2}}]}];c = RegionCentroid[ℛ]Show[ℛ, Graphics[{Red, Point[c]}]]ℛ = DelaunayMesh[RandomReal[1, {20, 3}]];c = RegionCentroid[ℛ]Show[HighlightMesh[ℛ, Style[2, Opacity[0.15]]], Graphics3D[{Red, PointSize[Medium], Point[c]}]]BoundaryMeshRegion 的几何中心：
ℛ = ConvexHullMesh[RandomReal[1, {10, 2}]];c = RegionCentroid[ℛ]Show[ℛ, Graphics[{Red, Point[c]}]]ℛ = ConvexHullMesh[RandomReal[1, {20, 3}]];c = RegionCentroid[ℛ]Show[HighlightMesh[ℛ, Style[2, Opacity[0.25]]], Graphics3D[{Red, PointSize[Medium], Point[c]}]]导出区域 (5)
RegionIntersection 的几何中心：
ℛ = RegionIntersection[Disk[{0, 0}, 1], Disk[{0, 1}, 1]];c = RegionCentroid[ℛ]Show[DiscretizeRegion[ℛ], Graphics[{Red, Point[c]}]]TransformedRegion 的几何中心：
ℛ = TransformedRegion[Disk[{0, 0}, 1], ShearingTransform[30 Degree, {1, 0}, {0, 1}]];c = RegionCentroid[ℛ]Show[DiscretizeRegion[ℛ, {{-2, 2}, {-1, 1}}], Graphics[{Red, Point[c]}]]RegionBoundary 的几何中心：
ℛ = RegionBoundary[Simplex[2]]c = RegionCentroid[ℛ]Show[DiscretizeRegion[ℛ, {{-1.1, 1.1}, {-1.1, 1.1}}], Graphics[{Red, Point[c]}]]
{r1, r2, r3} = {Disk[], ParametricRegion[{{u v, u ^ 2 - v ^ 2}, -1 ≤ u + v ≤ 1}, {u, v}], Simplex[{{0, 0}, {0, 1}, {1, 0}}]};RegionCentroid[BooleanRegion[#1 && (#2 || !#3)&, {r1, r2, r3}]]//Together
ℛ = InverseTransformedRegion[Disk[], {Indexed[#1, 1] + Indexed[#1, 2] + 1, Indexed[#1, 1] - Indexed[#1, 2] + 2}& , 2]RegionCentroid[ℛ]地理区域 (2)
Polygon 与 GeoPosition 一起使用所得边界多边形的质心：
ℛ = Polygon[GeoPosition[{{{40.083441, -88.235716}, {40.083607, -88.257488}, {40.082603, -88.257149},
{40.076136999999996, -88.25740499999999}, {40.076178, -88.270888}, {40.076516, -88.271558},
{40.083686, -88.271512}, {40.083659999999995, -88.267046}, ... 33323}, {40.098112, -88.228687},
{40.095216, -88.228627}, {40.095179, -88.238547}, {40.094480999999995, -88.238546},
{40.094508999999995, -88.23267}, {40.094106, -88.232556}, {40.090666999999996, -88.232477},
{40.090741, -88.235745}}}]];RegionCentroid[ℛ]Polygon 与 GeoGridPosition 一起使用所得边界多边形的质心：
ℛ = Polygon[GeoGridPosition[{{{-0.9950503945490105, 1.2366760550756015},
{-0.9952074890903578, 1.2369207053693891}, {-0.9952196732768064, 1.2369073327446167},
{-0.9953160063787643, 1.236848436956935}, {-0.9954141759436825, 1.2369993898475449},
{-0. ... 197645333103}, {-0.9949098578570917, 1.2368130881428654},
{-0.9948663952535768, 1.2367477711687371}, {-0.9948714472169538, 1.2367426500757825},
{-0.9949211061652593, 1.2367089232486177}, {-0.9949439717990124, 1.236746107097628}}}, "Bonne"]];RegionCentroid[ℛ]CSG 区域 (2)
二维空间中 CSGRegion 的几何中心：
ℛ = CSGRegion["Difference", {Disk[], Disk[{0.5, 0.5}]}];c = RegionCentroid[ℛ]Show[ℛ, Graphics[{Red, Point[c]}]]三维空间中 CSGRegion 的几何中心：
ℛ = CSGRegion["Difference", {Cube[3], Cuboid[{-1, -3, -1}, {3, 3, 3}]}];c = RegionCentroid[ℛ]Show[ℛ, Graphics3D[{Red, Point[c]}]]细分区域 (2)
二维空间中 SubdivisionRegion 的几何中心：
ℛ = SubdivisionRegion[Rectangle[]];c = RegionCentroid[ℛ]Show[ℛ, Graphics[{Red, Point[c]}]]三维空间中 SubdivisionRegion 的几何中心：
ℛ = SubdivisionRegion[Cube[]];c = RegionCentroid[ℛ]Show[Region[ℛ, BaseStyle -> {FaceForm[Opacity[0.2]]}], Graphics3D[{Red, Point[c]}]]应用 (5)
gm = ExampleData[{"Geometry3D", "Cow"}, "MeshRegion"]c = RegionCentroid[gm]Show[MeshRegion[gm, BaseStyle -> Opacity[.4]], Graphics3D[{Red, Point@c}]]
ℛ = Disk[];c1 = RegionCentroid[ℛ]
c2 = Integrate[{x, y}(x - 1)^2(y - 1)^2, {x, y}∈ℛ] / Area[ℛ]Legended[Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[c2], Blue, Point[c1]}], PointLegend[{Red, Blue}, {"Center of Mass", "Centroid"}]]ContourPlot[(x - 1)^2(y - 1)^2, {x, y}∈ℛ]pts = {a, b, c} = {{1, 2}, {0, 0}, {3, 0}};circumCenter = RegionCentroid[Circumsphere[pts]];bisector = Line[{circumCenter, RegionCentroid[Line[{a, b}]]}];Graphics[{{LightGray, Circumsphere[pts]}, {LightBlue, Triangle[pts]}, {Dashed, Red, bisector}, {Blue, Point[pts]}, {Red, PointSize[Large], Point[circumCenter]}}]pts = RandomReal[1, {100, 2}];ℛ = VoronoiMesh[pts, {{0, 1}, {0, 1}}];定义一个函数，计算沃罗诺伊网格的每个沃罗诺伊区域的几何中心：
vcf[pts_] := RegionCentroid /@ MeshPrimitives[VoronoiMesh[pts, {{0, 1}, {0, 1}}], "Faces"];对先导的沃罗诺伊区域的几何中心递归应用 VoronoiMesh：
centroids = NestList[vcf, pts, 3];vm = VoronoiMesh[#, {{0, 1}, {0, 1}}]& /@ centroids;每个沃罗诺伊区域生成点（黑色）向着区域的几何中心 （红色）收敛：
MapThread[Show[#1, Graphics[{Black, Point[#2], Red, Point[vcf[#2]]}]]&, {vm, centroids}]对区域的点的随机抽样取 Mean，估算区域的几何中心：
ℛ = ConvexHullMesh[RandomReal[1, {10, 2}]];
mf = RegionMember[ℛ];
pts = Select[RandomVariate[UniformDistribution[RegionBounds[ℛ]], 1000], mf];
Show[ℛ, Graphics[Point[pts]]]{c1, c2} = {Mean[pts], RegionCentroid[ℛ]}Show[ℛ, Graphics[{Red, Point[c1], Black, Point[c2]}]]属性和关系 (3)
RegionCentroid 不一定在区域内如果该区域不是凸的：
ℛ = Polygon[{{0, 0}, {3, -1}, {1, 0}, {3, 1}}];
c = RegionCentroid[ℛ];
Graphics[{LightBlue, EdgeForm[Gray], ℛ, Red, Point[c]}]RegionCentroid 等同于 Integrate[p,p∈ℛ]/m 且 m=RegionMeasure[ℛ]：
ℛ = Sphere[{1, 2, 3}];
m = RegionMeasure[ℛ];{RegionCentroid[ℛ], Integrate[p, p∈ℛ] / m}
{Subscript[ℛ, 1], Subscript[ℛ, 2]} = {Disk[{0, 0}], Disk[{2, 0}]};{m1, m2} = RegionMeasure /@ {Subscript[ℛ, 1], Subscript[ℛ, 2]};
{c1, c2} = RegionCentroid /@ {Subscript[ℛ, 1], Subscript[ℛ, 2]};(m1 c1 + m2 c2) / (m1 + m2)RegionCentroid[RegionUnion[Subscript[ℛ, 1], Subscript[ℛ, 2]]]//Simplify可能存在的问题 (1)
对于具有无限 RegionMeasure 的区域，RegionCentroid 返回带有 RegionMeasure 坐标的点：
ℛ = HalfSpace[{1, 1}, 0];RegionMeasure[ℛ]RegionCentroid[ℛ]
Wolfram Research (2014)，RegionCentroid，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionCentroid.html.
文本
Wolfram Research (2014)，RegionCentroid，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionCentroid.html.
CMS
Wolfram 语言. 2014. "RegionCentroid." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RegionCentroid.html.
APA
Wolfram 语言. (2014). RegionCentroid. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RegionCentroid.html 年