WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

Rotate[g,θ]

境界ボックスの中央で反時計回りに θ ラジアン回転された2Dグラフィックスプリミティブあるいはその他の任意のオブジェクト g を表す．

Rotate[g,θ,{x,y}]

点{x,y}の回りで回転させる．

Rotate[g,{u,v}]

原点の回りを回転させて2Dあるいは3Dベクトル u を v に変換する．

Rotate[g,θ,w]

原点に固定された3Dベクトル w の回りで3Dグラフィックスプリミティブを θ ラジアン回転させる．

Rotate[g,θ,w,p]

p に固定された3Dベクトル w の回りを回転させる．

Rotate[g,θ,{u,v}]

3Dベクトル u と v で定義される平面上で角度 θ 回転させる．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
関連するガイド
関連するワークフロー
関連リンク
履歴
引用書式

Rotate

Rotate[g,θ]

境界ボックスの中央で反時計回りに θ ラジアン回転された2Dグラフィックスプリミティブあるいはその他の任意のオブジェクト g を表す．

Rotate[g,θ,{x,y}]

点{x,y}の回りで回転させる．

Rotate[g,{u,v}]

原点の回りを回転させて2Dあるいは3Dベクトル u を v に変換する．

Rotate[g,θ,w]

原点に固定された3Dベクトル w の回りで3Dグラフィックスプリミティブを θ ラジアン回転させる．

Rotate[g,θ,w,p]

p に固定された3Dベクトル w の回りを回転させる．

Rotate[g,θ,{u,v}]

3Dベクトル u と v で定義される平面上で角度 θ 回転させる．

詳細とオプション

  • θ Degreeすなわち θ°は角度を度で指定する．
  • Rotateがグラフィックスの外側に現れた場合，Rotate[g,θ]中のオブジェクト g 等は任意の式でよい．
  • g の境界ボックス内で{Left,Bottom}のような特別な点を指定することができる．
  • x の位置はLeft，CenterあるいはRightとして指定できる．y の位置はBottom，CenterあるいはTopとして指定できる．
  • Rotateがグラフィックス内に現れた場合，座標{x,y}はグラフィックスの座標系内にあるとみなされる．
  • Rotateがグラフィックスの外側に現れた場合，座標{x,y}は回転されているオブジェクトの境界ボックスの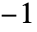から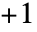の範囲にあるとみなされる．
  • Rotate[g,θ]はRotate[g,θ,{Center,Center}]に等しい．
  • スケールされた座標Scaled[{x,y}]で指定されたオブジェクトについては，Rotateは実質的に対応する通常の座標に対して変換を適用する．
  • Rotateがグラフィックス内に現れた場合，Normal[expr]は，可能であれば，すべてのRotate[gi,…]構文を座標系が明示的に変換された giのバージョンで置き換える．

例題

すべて開く すべて閉じる

例  (3)

正方形を30°回転させる：

直方体を 軸に沿って30° 回転させる：

テキストを45°回転させる：

スコープ  (8)

2Dの形に適用された変換：

3Dの形に適用された変換：

点に固定されたベクトルの周りの回転：

ベクトルをベクトルにマップする回転：

ベクトルとで定義された平面での回転：

テキストを回転させる：

スケールされた座標のオブジェクトを回転させる：

長方形の下方右のコーナーを固定する：

アプリケーション  (2)

垂直方向のテキストが入った格子：

ダイヤモンド格子：

特性と関係  (1)

Normalは可能であれば座標を明示的に変換する：

考えられる問題  (4)

デフォルトで，Rotateは境界ボックスの中心を回転の中心として使う：

回転の中心を明示的に指定する：

変換によってオブジェクトが見えなくなることがある：

PlotRangeを調整して変換されたオブジェクトを表示する：

回転されたテキストのベースラインの中心は周囲のテキストのベースラインと揃う：

別の揃え方については，回転の明示的な中心を指定する：

テキストの境界ボックスは常に直線的なので，連続する回転によって余分な空間が導入されることがある：

おもしろい例題  (2)

正多角形の回転：

ネストして回転された平方根：

Wolfram Research (2007), Rotate, Wolfram言語関数， https://reference.wolfram.com/language/ref/Rotate.html （2008年に更新）.

テキスト

Wolfram Research (2007), Rotate, Wolfram言語関数， https://reference.wolfram.com/language/ref/Rotate.html （2008年に更新）.

CMS

Wolfram Language. 2007. "Rotate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Rotate.html.

APA

Wolfram Language. (2007). Rotate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rotate.html

BibTeX

@misc{reference.wolfram_2025_rotate, author="Wolfram Research", title="{Rotate}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Rotate.html}", note=[Accessed: 18-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_rotate, organization={Wolfram Research}, title={Rotate}, year={2008}, url={https://reference.wolfram.com/language/ref/Rotate.html}, note=[Accessed: 18-September-2025]}