TransformedRegion

TransformedRegion[reg,f]

変換された領域を表す．ただし，reg は領域であり f は関数である．

詳細とオプション

例題

すべて開くすべて閉じる

例  (2)

回転された長方形：

で変換された円板：

スコープ  (24)

特別な領域  (10)

変換された領域の中には明示的に計算されたものがある：

変換を可視化する：

単位球体の一次分数変換：

変換を可視化する：

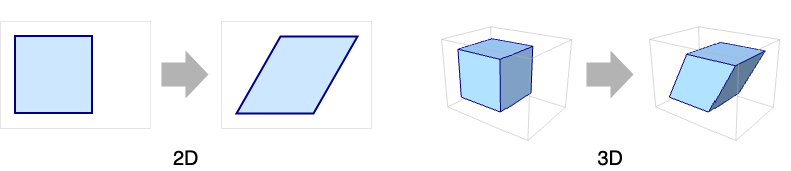
単位Diskを変換する：

点の帰属判定：

点の帰属条件：

単位Rectangleをせん断する：

RegionBoundsを計算する：

標準的なTriangleを回転させる：

領域は一定で有界のままである：

Circleをスケールする：

ArcLengthを計算する：

非線形変換で変換された円板：

Indexedを使って同じ点のマッピングを表す：

RegionMeasureを計算する：

非線形変換によって，3DのCuboidから2Dに点をマップする：

幾何次元と埋込み次元：

RegionCentroidを計算する：

可視化する：

点からの符号付き距離：

3DのCuboidを回転させる：

点からの距離：

領域内の最近点：

最近点：

回転された単位立方体上で積分する：

最適化する：

方程式を解く：

数式定義領域  (6)

ParametricRegionをせん断する：

ArcLengthを計算する：

指定された点からの領域内の最近点：

回転されたParametricRegion：

Areaを計算する：

RegionBoundsを計算する：

RegionDistance：

ImplicitRegionをせん断する：

領域は非有界のままである：

点の帰属判定：

点の帰属条件：

ImplicitRegionをスケールする：

Volumeを計算する：

領域上で積分(Integrate)する：

最適化：

方程式を解く：

非線形変換によって変換されたImplicitRegion：

Indexedを使って同じ点のマッピングを表す：

RegionMeasureを計算する：

非線形変換による3D球体から2Dへの点のマッピング：

幾何次元と埋込み次元：

RegionCentroidを計算する：

可視化：

メッシュ領域  (3)

BoundaryMeshRegionを回転させる：

変換された領域もBoundaryMeshRegionQである：

点の帰属判定：

RegionCentroidを計算する：

これを可視化する：

Areaを計算する：

この領域上で積分する：

MeshRegionをせん断する：

変換された領域もMeshRegionQである：

Volumeを計算する：

RegionBoundsを計算する：

点からのRegionDistance：

領域上で積分(Integrate)する：

低次元MeshRegionをスケールする：

ArcLengthを計算する：

領域上の，指定された点からの最近点：

派生領域  (5)

TransformedRegionを変換する：

Volumeを計算する：

領域上で積分(Integrate)する：

最適化：

方程式を解く：

RegionDifferenceを変換する：

Areaを計算する：

RegionBoundsを計算する：

指定された点からのSignedRegionDistance：

RegionBoundaryを変換する：

ArcLengthを計算する：

領域上の，指定された点からの最近点：

RegionProductを変換する：

Volumeを計算する：

RegionBoundsを計算する：

点からのRegionDistance：

非線形変換によって，RegionUnionを変換する：

Indexedを使って同じ点のマッピングを表す：

RegionBoundsを計算する：

アプリケーション  (2)

任意の三角形は標準的な三角形のアフィン変換である：

この変換は で与えられる．ただし，A=TemplateBox[{{{, {{{p, _, 1}, -, {p, _, 0}}, ,, ..., ,, {{p, _, 3}, -, {p, _, 0}}}, }}}, Transpose]である：

もとの単位三角形と変換された単位三角形を比較する：

中心がの単位Cuboidの透視変換を求める：

この領域を可視化する：

Volumeを計算する：

Wolfram Research (2014), TransformedRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/TransformedRegion.html.

テキスト

Wolfram Research (2014), TransformedRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/TransformedRegion.html.

CMS

Wolfram Language. 2014. "TransformedRegion." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TransformedRegion.html.

APA

Wolfram Language. (2014). TransformedRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransformedRegion.html

BibTeX

@misc{reference.wolfram_2024_transformedregion, author="Wolfram Research", title="{TransformedRegion}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/TransformedRegion.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_transformedregion, organization={Wolfram Research}, title={TransformedRegion}, year={2014}, url={https://reference.wolfram.com/language/ref/TransformedRegion.html}, note=[Accessed: 21-November-2024 ]}