Triangle
Triangle[{p1,p2,p3}]
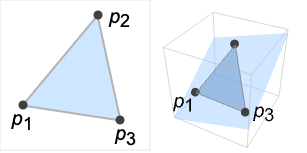
represents a filled triangle with corner points p1, p2, and p3.
Triangle[{{p11,p12,p13},…}]
represents a collection of triangles.
Details and Options

- Triangle can be used as a geometric region and a graphics primitive.
- Triangle represents a planar region consisting of all convex combinations of corner points pi,
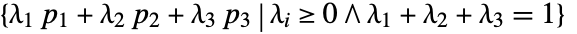 .
. - Triangle[] is equivalent to Triangle[{{0,0},{1,0},{0,1}}].
- CanonicalizePolygon can be used to convert a triangle to an explicit Polygon object.
- As a geometric region, the points pi can have any length.
- Triangle can be used in Graphics and Graphics3D.
- In graphics, the points pi can be Scaled, Offset, ImageScaled, and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Texture, and color.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures - Triangle can be used with symbolic points in GeometricScene.
Background & Context
- Triangle[{p1,p2,p3}] represents the filled triangle with vertices p1, p2 and p3, where each pi is specified as a list with length corresponding to the embedding dimension. Most commonly, the vertices of a Triangle are lists of length two (giving a triangle in the 2D plane) or three (giving a triangle embedded in 3D space). The zero-argument form Triangle[] evaluates to the standard 2-simplex Triangle[{{0,0},{1,0},{0,1}}]. The syntax Triangle[{{p11,p12,p13},…,{pk1,pk2,pk3}}] may be used to represent a multi-triangle collection.
- Triangle objects can be visually formatted in two and three dimensions using Graphics and Graphics3D, respectively. As with other graphics primitives, the appearance of Triangle objects in graphics can be modified by specifying edge and face directives EdgeForm and FaceForm, color directives such as Red, the transparency directive Opacity and the style option Antialiasing. Texture may be used to apply objects as textures on the faces of Triangle objects, and the options VertexColors, VertexNormals and VertexTextureCoordinates may be used to apply additional formatting.
- Triangle may also serve as a region specification over which a computation should be performed. RegionMeasure (and Area) returns the area of a Triangle object, while RegionDimension and RegionEmbeddingDimension return 2 and Length[pi], respectively, for Triangle[{p1,p2,p3}]. In addition, GeometricTransformation and more specific transformation functions such as Translate and Rotate can be used to represent the result of applying relevant geometric transformations to a Triangle.
- Triangle is related to a number of other symbols. AASTriangle, SSSTriangle, ASATriangle and SASTriangle return two-dimensional Triangle objects constructed using relevant side and angle specifications. Triangle is a special case of both Polygon and Simplex, in the sense that Triangle[{p1,p2,p3}] is equivalent to both Polygon[{p1,p2,p3}] and Simplex[{p1,p2,p3}]. The three-dimensional simplex generalization of Triangle is implemented as Tetrahedron.
Examples
open allclose allBasic Examples (4)
Different styles applied to Triangle:
Scope (18)
Graphics (8)
Styling (2)
Coordinates (3)
Applications (6)
The standard simplex and Kuhn simplex in 2D are triangles:
Define an equilateral triangle by side length:
Compute its Area:
Equivalently use SSSTriangle:
Define an isosceles triangle by base length and height:
Compute its Area:
Find a perpendicular bisector of a triangle:
Visualize circumcenter and bisectors in red:
One way of measuring the quality of a triangle is the radius/edge ratio:
A lower ratio indicates that the triangle will not be unusually thin:
Properties & Relations (5)
Triangle is a special case of Polygon:
Triangle is a special case of Simplex:
ImplicitRegion can represent any Triangle region:
ParametricRegion can represent any Triangle region:
BoundaryMeshRegion can represent any Triangle region:
Text
Wolfram Research (2014), Triangle, Wolfram Language function, https://reference.wolfram.com/language/ref/Triangle.html (updated 2019).
CMS
Wolfram Language. 2014. "Triangle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Triangle.html.
APA
Wolfram Language. (2014). Triangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Triangle.html