Triangle
詳細とオプション

- Triangleは,幾何領域としてあるいはグラフィックスプリミティブとして使うことができる.
- Triangleは,すべての角の点 pi が凸である組合せからなる平面領域,つまり
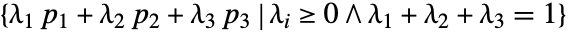 を表す.
を表す. - Triangle[]はTriangle[{{0,0},{1,0},{0,1}}]に等しい.
- CanonicalizePolygonを使って三角形を明示的なPolygonオブジェクトに変換できる.
- 幾何学的な領域としては,点 pi は,任意の長さでよい.
- Triangleは,GraphicsおよびGraphics3Dで使える.
- グラフィックスでは,点 pi は,Scaled,Offset,ImageScaled,Dynamicのいずれの式でもよい.
- グラフィックスの描画は,FaceForm,EdgeForm,Texture,色等の指示子に影響される.
- グラフィックスで使える設定とオプション
-
VertexColors Automatic 補間される頂点の色 VertexNormals Automatic 陰影のための有効な頂点の法線 VertexTextureCoordinates None テクスチャのための座標 - Triangleは,GeometricSceneの記号的な点と一緒に使うことができる.
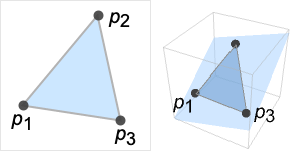
予備知識
- Triangle[{p1,p2,p3}]は,頂点が p1,p2,p3の塗り潰された三角形を表す.各 piは埋込み次元に対応する長さのリストとして指定される.通常,Triangleの頂点は,長さ2のリスト(2D平面の三角形)あるいは長さ3のリスト(3D空間に埋め込まれた三角形)である.引数のない形のTriangle[]を評価すると,標準的な2単体Triangle[{{0,0},{1,0},{0,1}}]になる.シンタックスTriangle[{{p11,p12,p13},…,{pk1,pk2,pk3}}]を使って複数の三角形の集合を表すことができる.
- Triangleオブジェクトは,GraphicsおよびGraphics3D, を使って,それぞれ2Dおよび3Dで視覚的にフォーマットすることができる.Triangleオブジェクトの外観は,他のグラフィックスプリミティブと同じように,辺と面の指示子EdgeFormおよびFaceForm,Redのような色指示子,透過性指示子Opacity,スタイルオプションAntialiasingを指定して変更することができる.Textureを使ってTriangleオブジェクトの表面のテクスチャとしてオブジェクトを適用することができ,オプション VertexColors,VertexNormals,VertexTextureCoordinatesを使って追加的なフォーマットを行うことができる.
- Triangleは計算を行う領域の指定にも使うことができる.Triangle[{p1,p2,p3}]に対してRegionMeasure(およびArea)はTriangleオブジェクトの面積を返すのに対し,RegionDimensionおよびRegionEmbeddingDimensionは,それぞれ2およびLength[pi]を返す.これに加え,GeometricTransformation,あるいはTranslateやRotateのようにより特殊な変換関数を使って,Triangleに適切な幾何変換を適用した結果を表すことができる.
- Triangleは他の多くのシンボルと関連している.AASTriangle,SSSTriangle,ASATriangle,SASTriangleは,適切な辺と角の指定を使って構築した二次元のTriangleオブジェクトを返す.Triangleは,Triangle[{p1,p2,p3}]がPolygon[{p1,p2,p3}]とSimplex[{p1,p2,p3}]の両方と等価であるという意味で,PolygonとSimplexの両方の特殊ケースである.Triangleの三次元単体一般化はTetrahedronとして実装されている.
例題
すべて開く すべて閉じる例 (4)
スコープ (18)
グラフィックス (8)
座標 (3)
アプリケーション (6)
特性と関係 (5)
ImplicitRegionは,任意のTriangleの領域を表すことができる:
ParametricRegionは,任意のTriangleの領域を表すことができる:
BoundaryMeshRegionは,任意のTriangleの領域を表すことができる:
関連項目
Polygon AASTriangle SSSTriangle ASATriangle SASTriangle Tetrahedron Simplex GeometricScene
形式: STL
Function Repository: Orthocenter HeronFormula LucasCircles NagelPoint EulerLinePoints LemoineInellipse
テキスト
Wolfram Research (2014), Triangle, Wolfram言語関数, https://reference.wolfram.com/language/ref/Triangle.html (2019年に更新).
CMS
Wolfram Language. 2014. "Triangle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Triangle.html.
APA
Wolfram Language. (2014). Triangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Triangle.html
BibTeX
@misc{reference.wolfram_2025_triangle, author="Wolfram Research", title="{Triangle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Triangle.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_triangle, organization={Wolfram Research}, title={Triangle}, year={2019}, url={https://reference.wolfram.com/language/ref/Triangle.html}, note=[Accessed: 07-February-2026]}

