VonMisesDistribution
VonMisesDistribution[μ,κ]
平均 μ,集中度 κ のvon Mises分布を表す.
詳細
- von Mises分布における値
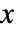 の確率密度は,
の確率密度は,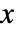 が
が 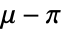 から
から 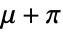 までのとき
までのとき 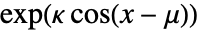 に比例する.
に比例する. - VonMisesDistributionでは,μ は任意の実数でよく,κ は任意の非負の実数でよい.
- VonMisesDistributionでは,μ と κ は任意の無次元量でよい. »
- VonMisesDistributionは,Mean,CDF,RandomVariate等の関数とともに用いることができる.
予備知識
- VonMisesDistribution[μ,κ]は,区間
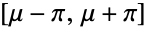 上でサポートされ,実数 μ(分布の平均)および非負の実数 κ(分布の集中度)によってパラメータ化された連続統計分布表す.この2つは,ともに確率密度関数(PDF)の全体的な動作を決定する.von Mises分布のPDFは単一の峰(大域的最大値)がある単峰性であることが多いが,その全体的な形(高さ,広がり,最大値の水平位置)は μ と κ の値によって決定される.von Mises分布は,円形正規分布あるいはTikhonov分布と呼ばれることがある.
上でサポートされ,実数 μ(分布の平均)および非負の実数 κ(分布の集中度)によってパラメータ化された連続統計分布表す.この2つは,ともに確率密度関数(PDF)の全体的な動作を決定する.von Mises分布のPDFは単一の峰(大域的最大値)がある単峰性であることが多いが,その全体的な形(高さ,広がり,最大値の水平位置)は μ と κ の値によって決定される.von Mises分布は,円形正規分布あるいはTikhonov分布と呼ばれることがある. - von Mises分布は1900年代の初めに提唱され,1918年にドイツの数学者・統計学者であるRichard von Misesによる論文で,当時知られていた化学元素の原子の重みの分布をモデル化するツールの統計学モデルとして導入された.von Mises分布は,実線上で定義されたNormalDistributionの円形版で,円形統計学の分野で最も研究された分布の一つである.これは,一般化され,数多くのコンテキストでモデリングツールとして適用されてきた.特に,von Mises分布は,病気の蔓延,タンパク質データ,信号処理における干渉アライメント,機械学習におけるプライバシー保護アルゴリズム等の現象のモデル化に使われてきている.
- RandomVariateを使って,von Mises分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,VonMisesDistribution[μ,κ]](より簡略な表記では xVonMisesDistribution[μ,κ])を使って,確率変数 x がvon Mises分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[VonMisesDistribution[μ,κ],x]およびCDF[VonMisesDistribution[μ,κ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がvon Mises分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックvon Mises分布を推定することが,FindDistributionParametersを使ってデータをベータ分布にフィットすることができる.ProbabilityPlotを使って記号von Mises分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号von Mises分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたvon Mises分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってvon Mises分布を含む高次元分布を構築することが,ProductDistributionを使ってvon Mises分布を含む独立成分分布の結合分布を計算することができる.
- VonMisesDistributionは数多くの分布と関係がある.VonMisesDistributionは,VonMisesDistribution[μ,0]のPDFがUniformDistribution[{μ-π,μ+π}] のPDFと厳密に等しいという意味でUniformDistributionを直接一般化したものであり,VonMisesDistributionのPDFが κ→∞ のときにNormalDistributionのPDFに近付くという意味でNormalDistributionの極限でもある.VonMisesDistributionは,WignerSemicircleDistribution,LogNormalDistribution,HalfNormalDistribution,BinormalDistribution,InverseGaussianDistributionとも密接な関係がある.
例題
すべて開くすべて閉じるスコープ (5)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元のQuantityを使ってVonMisesDistributionを定義する:
特性と関係 (3)
Wolfram Research (2010), VonMisesDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/VonMisesDistribution.html (2016年に更新).
テキスト
Wolfram Research (2010), VonMisesDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/VonMisesDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "VonMisesDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/VonMisesDistribution.html.
APA
Wolfram Language. (2010). VonMisesDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VonMisesDistribution.html