WeibullDistribution

WeibullDistribution[α,β]

形状母数 α，尺度母数 β のワイブル(Weibull)分布を表す．

WeibullDistribution[α,β,μ]

形状母数 α，尺度母数 β，位置母数 μ のワイブル分布を表す．

詳細

  • WeibullDistributionはRosin–Rammler分布としても知られている．
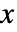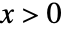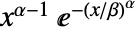  • ワイブル分布における値 の確率密度は，のときは に比例し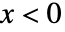，のときは0になる． »
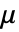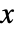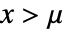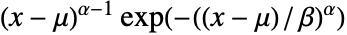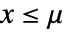  • 位置母数 のワイブル分布における値 の確率密度は， のときはに比例し のときは0である．
  • WeibullDistributionでは，α と β は任意の正の実数でよく，μ は任意の実数でよい．
  • WeibullDistributionでは，β と μ は単位次元が等しい任意の数量でよく，α は無次元量でよい． »
  • WeibullDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • WeibullDistribution[α,β,μ]は，区間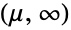上でサポートされ，実数 μ（「位置母数」と呼ばれる）および正の実数で α と β（それぞれ「形状母数」および「尺度母数」と呼ばれる）でパラメータ化された連続統計分布を表す．これらの母数は，ともに分布の確率密度関数(PDF)の動作を決定する．ワイブル分布のPDFは，α，β，μ の値によって，単一の「峰」（大域的最大値）を持つ単峰性，領域の下端に潜在的特異値が近付く単調減少等を含む任意の形になる．加えて，PDFの裾部は，α，β，μ の値によって「太い」（つまり，PDFは 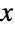の大きい値について非指数的に減少する）か「薄い」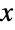（ の大きい値についてPDFが指数的に減少する）．この動作は，分布のSurvivalFunctionを分析することで量的に厳密にすることができる．ワイブル分布は，Rosin–Rammler分布と呼ばれることがある．母数が2つの形WeibullDistribution[α,β]はWeibullDistribution[α,β,0]に等しい．
  • WeibullDistributionは，「極値分布」と分類される4つの分布の一つである（他の3つはFrechetDistribution，ExtremeValueDistribution，GumbelDistribution）．極値分布はすべて「非常に珍しい」，中央値から甚だしく外れたデータ集合からなる）「極端な」あるいは「稀な」事象の数量化のためのツールとして使われる．ワイブル分布は，1920年代にFréchetが発見したが，スウェーデン人の科学者であるWaloddi Weibullに因んで名付けられた．ワイブル分布は，そのはじめから，粒子サイズの分布や風速，洪水，旱魃，壊滅的な保険損失等を含む数多くの現実世界の事象のモデル化に使われて来た．ワイブル分布は，生存分析，製造業，工学，保険数理等にも使われている．
  • RandomVariateを使って，ワイブル分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,WeibullDistribution[α,β,μ]]（より簡略な表記では xWeibullDistribution[α,β,μ]）を使って，確率変数 x がワイブル分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[WeibullDistribution[α,β,μ],x]およびCDF[WeibullDistribution[α,β,μ],x]を使って得られる．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がワイブル分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックワイブル分布を推定することが，FindDistributionParametersを使ってデータをワイブル分布にフィットすることができる．ProbabilityPlotを使って記号ワイブル分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号ワイブル分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたワイブル分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってワイブル分布を含む高次元分布を構築することが，ProductDistributionを使ってワイブル分布を含む独立成分分布の結合分布を計算することができる．
  • WeibullDistributionは他のいくつかの分布と関係がある．上述のように，WeibullDistributionはExtremeValueDistribution，FrechetDistribution，GumbelDistributionと定性的関係を共有している．これらの関係はWeibullDistributionのPDFがExtremeValueDistribution，FrechetDistribution，GumbelDistributionの変換(TransformedDistribution)として実現できることに注目することで，定量化することができる．WeibullDistributionは，WeibullDistribution[1,1/λ]のCDFおよびWeibullDistribution[2, 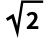σ]のPDFがそれぞれExponentialDistribution[λ]のCDFおよびRayleighDistribution[σ]のPDFと等しいという意味で，ExponentialDistributionとRayleighDistributionの両方の一般化である．WeibullDistributionは，MinStableDistribution，MaxStableDistribution，GammaDistribution，GompertzMakehamDistributionとも密接な関係がある．

例題

すべて開くすべて閉じる

例  (5)

確率密度関数：

位置母数あり：

累積分布関数：

位置母数あり：

平均：

分散：

中央値：

スコープ  (8)

ワイブル分布から擬似乱数のサンプルを生成する：

そのヒストグラムと確率密度関数を比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度は第1母数のみに依存する：

極限値：

尖度は第1母数のみに依存する：

尖度は最小値に達する：

極限値：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

FactorialMoment：

Cumulant：

ハザード関数：

位置母数あり：

分位関数：

位置母数あり：

母数でQuantityを一貫して使うとQuantityDistributionが返される：

四分位点を計算する：

アプリケーション  (8)

ある部品の寿命が，，で時間単位で与えられるWeibullDistributionに従っている．この部品が300時間使用可能である確率を求める：

この部品のうち300時間を経過しても使用可能なものが500時間経っても使用可能である確率を求める：

故障までの平均時間を求める：

独立した30個のこのような部品の故障までの時間のシミュレーションを行う：

あるデバイスの寿命はWeibullDistributionに従う．このデバイスの信頼性を求める：

ハザード関数は α>1 と beta の任意の値について増加する：

直列のこのようなデバイス2つの信頼性を求める：

並列のこのようなデバイス2つの信頼性を求める：

両方の系の信頼性を と について比較する：

2つの工場で作られている部品がある．工場Aからの製品の寿命は ，のワイブル分布に従い，工場Bからの製品の故障までの時間は, と （単位：10年）のワイブル分布に従う．工場Aからの部品が工場Bからの部品よりも早く故障する確率を求める：

部品の60%は工場Aで製造されると仮定する．無作為に抽出した部品の故障までの時間の分布を求める：

故障までの平均時間を求める：

各工場の製品の故障までの平均時間を求める：

フェージングチャネル理論では，WeibullDistributionを使って800–900MHzの周波数範囲を使う移動無線システムのフェージング振幅のモデル化が行われる．瞬間的な信号対ノイズ比の分布を求める．ただし，， は記号あたりのエネルギー， はホワイトノイズのスペクトル密度である：

もWeibullDistributionに従うことを示す：

平均を求める：

フェージングの量を求める：

極限値：

WeibullDistributionを使って風速を近似することができる：

推定分布を求める：

その確率密度関数を風速データのヒストグラムと比較する：

風速が時速30キロより大きくなる日の確率を求める：

平均風速を求める：

1ヶ月間の毎日の平均風速のシミュレーションを行う：

ある場所では平均風速が秒速7メートルで形状母数2のワイブル分布に従うという：

結果の風速分布：

GE製1.5 MWの風力タービンの動力曲線：

1年間に生み出される総エネルギー量の平均は4.3GWhである：

年間最大の地震のマグニチュードはWeibullDistributionを使ってモデル化できる．アメリカ合衆国における過去200年間の地震について考察する：

年間最大値を求める：

欠測値を除きサンプルを作る：

ワイブル分布をサンプルにフィットする：

サンプルのヒストグラムを推定分布の確率密度関数と比較する：

モデルを使い，年間最大地震のマグニチュードが6以上である確率を求める：

年間最大地震の平均マグニチュードを求める：

30年間の年間最大地震のマグニチュードのシミュレーションを行う：

BenktanderWeibullDistributionと関連する定常更新分布を求める：

生存関数：

切断WeibullDistributionと比較する：

特性と関係  (18)

ワイブル分布は平行移動と正の因子によるスケーリングの下では閉じている：

WeibullDistributionの族は最小値の下では閉じている：

WeibullDistributionのCDFは最小安定化条件方程式を解く：

と を固定し簡約する：

WeibullDistributionのベキ乗もまたWeibullDistributionである：

すべてのモーメントが等しい：

ランダムサンプリングを通して確率密度関数を比較する：

他の分布との関係：

デフォルト位置は0である：

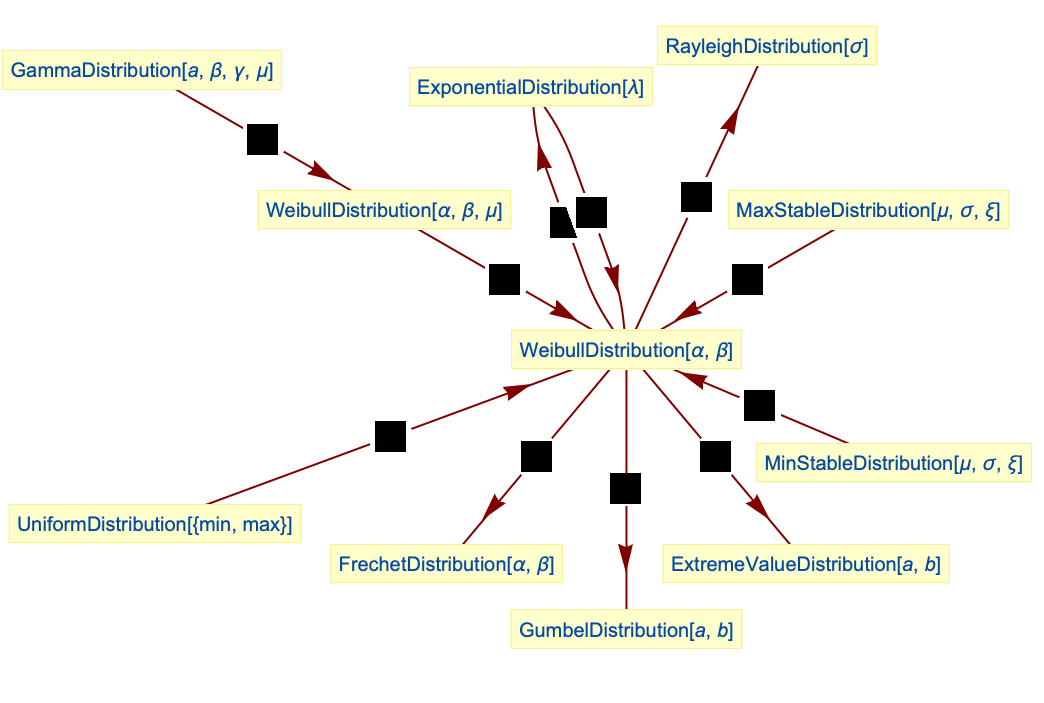
ワイブル分布はUniformDistributionを変換したものである：

WeibullDistributionはExtremeValueDistributionと指数関数的に関連している：

WeibullDistributionはGumbelDistributionと指数関数的に関連している：

ExponentialDistributionはワイブル分布の特殊ケースである：

RayleighDistributionはワイブル分布の特殊ケースである：

ワイブル分布はExponentialDistributionを変換したものである：

FrechetDistributionはワイブル分布を変換したものである：

ワイブル分布はMinStableDistributionの特殊ケースである：

ワイブル分布はMaxStableDistributionを変換したものである：

WeibullDistributionは一般化されたGammaDistributionの特殊ケースである：

GompertzMakehamDistributionは切断WeibullDistributionに関連している：

GompertzMakehamDistributionはワイブル分布に関連している：

考えられる問題  (3)

WeibullDistributionは，α あるいは β が正の実数ではないときは定義されない：

ワイブル分布の特性関数は，閉形式で表せない：

記号出力に無効な母数を代入すると無意味な結果が返される：

おもしろい例題  (1)

累積分布関数の等高線を持つ α のさまざまな値についての確率密度関数：

Wolfram Research (2007), WeibullDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeibullDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), WeibullDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/WeibullDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "WeibullDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/WeibullDistribution.html.

APA

Wolfram Language. (2007). WeibullDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WeibullDistribution.html

BibTeX

@misc{reference.wolfram_2024_weibulldistribution, author="Wolfram Research", title="{WeibullDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/WeibullDistribution.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_weibulldistribution, organization={Wolfram Research}, title={WeibullDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/WeibullDistribution.html}, note=[Accessed: 21-November-2024 ]}