WignerSemicircleDistribution
WignerSemicircleDistribution[r]
半径 r で原点を中心としたWignerの半円分布を表す.
WignerSemicircleDistribution[a,r]
半径 r で a を中心としたWignerの半円分布を表す.
詳細
- Wignerの半円分布における値
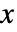 の確率密度は,
の確率密度は,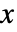 が
が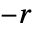 から
から 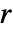 までの間では
までの間では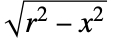 に比例する.
に比例する. - WignerSemicircleDistributionでは,a は任意の実数でよく,r は任意の正の実数でよい.
- WignerSemicircleDistributionでは,a と r は単位次元が等しい任意の数量でよい. »
- WignerSemicircleDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- WignerSemicircleDistribution[a,r]は,実数 a(分布の中心)と正の実数 r(その半径)によってパラメータ化された区間
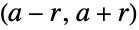 上でサポートされる連続統計分布を表す.これらの数は,ともに,確率密度関数(PDF)の全体的な動作を決定する.一般に,Wignerの半円分布の確率密度関数は楕円形をしており,したがって単一の峰(大域的最大値)を持つ単峰性であるが,その全体的な形(高さ,広がり,最大値の水平位置)は a および r の値によって決まる.母数が1つの形のWignerSemicircleDistribution[r]はWignerSemicircleDistribution[0,r]に等しい.Wignerの半円分布は,Sato–Tate分布,あるいは単にWigner分布と呼ばれることがある.
上でサポートされる連続統計分布を表す.これらの数は,ともに,確率密度関数(PDF)の全体的な動作を決定する.一般に,Wignerの半円分布の確率密度関数は楕円形をしており,したがって単一の峰(大域的最大値)を持つ単峰性であるが,その全体的な形(高さ,広がり,最大値の水平位置)は a および r の値によって決まる.母数が1つの形のWignerSemicircleDistribution[r]はWignerSemicircleDistribution[0,r]に等しい.Wignerの半円分布は,Sato–Tate分布,あるいは単にWigner分布と呼ばれることがある. - Wignerの半円分布は,ハンガリー系アメリカ人の科学者であるEugene Wignerに因んで命名された.無限ランダム行列に関する1955年のWignerの論文は,ランダム行列理論のコンテキストにおけるこの分布の重要性を示している.Wignerの半円分布はいわゆるWignerの半円則の統計的な基礎となっている.この法則は,量子力学におけるある種のクラスのランダム行列の固有値はWigner分布に従っていると述べている.この分布は線形代数,フーリエ級数,スペクトル解析を含む,統計量子力学やその他の力学のさまざまな下位分野における現象に応用されている.
- RandomVariateを使って,Wigner分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,WignerSemicircleDistribution[a,r]](より簡略な表記では xWignerSemicircleDistribution[a,r])を使って,確率変数 x がベータ分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[WignerSemicircleDistribution[a,r],x]およびCDF[WignerSemicircleDistribution[a,r],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がWigner分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックWigner分布を推定することが,FindDistributionParametersを使ってデータをWigner分布にフィットすることができる.ProbabilityPlotを使って記号Wigner分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Wigner分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたWigner分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってWigner分布を含む高次元分布を構築することが,ProductDistributionを使ってWigner分布を含む独立成分分布の結合分布を計算することができる.
- WignerSemicircleDistributionは他の多くの分布と関連している.この分布は,WignerSemicircleDistribution[r]の確率密度関数が r>0のときはPearsonDistribution[1,1,0,-1,0,r]のそれと厳密に等しいという意味で,PearsonDistributionによって一般化される.同様に,WignerSemicircleDistributionはBetaDistributionの変換TransformedDistribution)として実現できる.PDF[WignerSemicircleDistribution[r],x]は r→0のときDiracDelta[x] に近付く.WignerSemicircleDistributionはVonMisesDistributionおよびBetaPrimeDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (1)
平均が0で分散が有限である独立同分布に従う確率変数によって形成された大規模対称行列のスペクトル密度が,WignerSemicircleDistributionの確率密度関数に収束するという,Wignerの半円則についての普遍的予測を説明する:
要素がスチューデント ![]() 分布に従う行列のスペクトルのサンプルを取る:
分布に従う行列のスペクトルのサンプルを取る:
モーメント法を使ってWignerSemicircleDistributionをサンプルにフィットする:
特性と関係 (4)
WignerSemicircleDistributionは平行移動と正の因子によるスケーリングのもとでは閉じている:
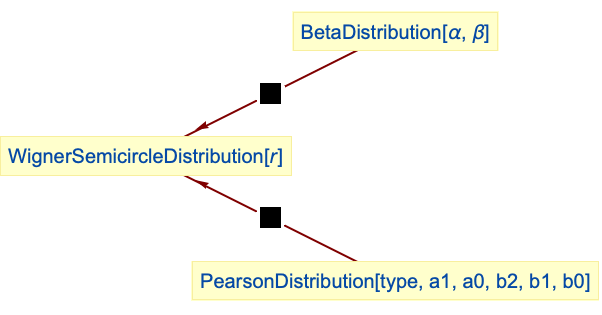
Wignerの半円分布はタイプ1のPearsonDistributionの特殊ケースである:
Wignerの半円分布は,特殊なBetaDistributionを変換したものである:
テキスト
Wolfram Research (2010), WignerSemicircleDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/WignerSemicircleDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "WignerSemicircleDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/WignerSemicircleDistribution.html.
APA
Wolfram Language. (2010). WignerSemicircleDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WignerSemicircleDistribution.html