ZTransform
ZTransform[expr,n,z]
expr のZ変換を与える.
ZTransform[expr,{n1,…,nm},{z1,…,zm}]
expr の多次元Z変換を与える.
詳細とオプション

- 離散関数
 のZ変換は
のZ変換は 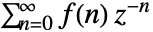 で与えられる.
で与えられる. - 多次元Z変換は
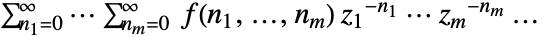 で与えられる.
で与えられる. - 使用可能なオプション
-
Assumptions $Assumptions パラメータに関する仮定 GenerateConditions False パラメータについての条件を持つ答を生成するかどうか Method Automatic 使用するメソッド VerifyConvergence True 収束を確かめるかどうか - TraditionalFormでは,ZTransformは を使って出力される.
例題
すべて開くすべて閉じるスコープ (25)
基本的な用法 (7)
Plot3D,ContourPlotあるいはDensityPlotを使って大きさをプロットする:
複素平面上のスペクトルをParametricPlot3Dを使ってプロットする:
ZTransformは線形性を含むいくつかの特性を使う:
ZTransformは自動的にリストに縫い込まれる:
TraditionalFormによる表示:
特殊数列 (13)
DiscreteRatioはすべての超幾何項数列について有理である:
特殊演算子 (5)
オプション (4)
Assumptions (1)
Assumptionsを使って与えられた範囲の方程式を得る:
GenerateConditions (1)
GenerateConditionsをTrueに設定して収束範囲を得る:
VerifyConvergence (1)
特性と関係 (6)
ZTransformはGeneratingFunctionと密接な関係がある:
ExponentialGeneratingFunction:
InverseZTransformを使って変換から数列を得る:
ZTransformは実質的に無限和を計算する:
考えられる問題 (1)
テキスト
Wolfram Research (1999), ZTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/ZTransform.html (2008年に更新).
CMS
Wolfram Language. 1999. "ZTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/ZTransform.html.
APA
Wolfram Language. (1999). ZTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZTransform.html