Manipulating Lists
Manipulating Lists
| Constructing Lists | Partitioning and Padding Lists |
| Manipulating Lists by Their Indices | Sparse Arrays: Manipulating Lists |
| Nested Lists |
| Range[n] | the list {1,2,3,…,n} |
| Table[expr,{i,n}] | the values of expr with i from 1 to n |
| Array[f,n] | the list {f[1],f[2],…,f[n]} |
| NestList[f,x,n] | {x,f[x],f[f[x]],…} with up to n nestings |
| Normal[SparseArray[{i1->v1,…},n]] | a length n list with element ik being vk |
| Apply[List,f[e1,e2,…]] | the list {e1,e2,…} |
SparseArray lets you specify values at particular positions:
Often you will know in advance how long a list is supposed to be, and how each of its elements should be generated. And often you may get one list from another.
| Table[expr,{i,list}] | the values of expr with i taking on values from list |
| Map[f,list] | apply f to each element of list |
| MapIndexed[f,list] | give f[elem,{i}] for the i th element |
| Cases[list,form] | give elements of list that match form |
| Select[list,test] | select elements for which test[elem] is True |
| Pick[list,sel,form] | pick out elements of list for which the corresponding elements of sel match form |
| TakeWhile[list,test] | |
| list[[{i1,i2,…}]] or Part[list,{i1,i2,…}] | |
give a list of the specified parts of list | |
Sometimes you may want to accumulate a list of results during the execution of a program. You can do this using Sow and Reap.
An alternative but less efficient approach involves introducing a temporary variable, then starting with t={}, and successively using AppendTo[t,elem].
| Part[list,spec] or list[[spec]] | part or parts of a list |
| Part[list,spec1,spec2,…] or list[[spec1,spec2,…]] | part or parts of a nested list |
| n | the n th part from the beginning |
| -n | the n th part from the end |
| {i1,i2,…} | a list of parts |
| m;;n | parts m through n |
| All | all parts |
You can use ;; to indicate all indices in a given range:
It is sometimes useful to think of a nested list as being laid out in space, with each element at a coordinate position given by its indices. There is then a direct geometrical interpretation for list[[spec1,spec2,…]]. If a given speck is a single integer, then it represents extracting a single slice in the k th dimension, while if it is a list, it represents extracting a list of parallel slices. The final result for list[[spec1,spec2,…]] is then the collection of elements obtained by slicing in each successive dimension.
Part is set up to make it easy to pick out structured slices of nested lists. Sometimes, however, you may want to pick out arbitrary collections of individual parts. You can do this conveniently with Extract.
| Part[list,{i1,i2,…}] | the list {list[[i1]],list[[i2]],…} |
| Extract[list,{i1,i2,…}] | the element list[[i1,i2,…]] |
| Part[list,spec1,spec2,…] | parts specified by successive slicing |
| Extract[list,{{i1,i2,…},{j1,j2,…},…}] | the list of individual parts {list[[i1,i2,…]],list[[j1,j2,…]],…} |
An important feature of Extract is that it takes lists of part positions in the same form as they are returned by functions like Position.
| Take[list,spec] | take the specified parts of a list |
| Drop[list,spec] | drop the specified parts of a list |
| Take[list,spec1,spec2,…]
,
Drop[list,spec1,spec2,…] | take or drop specified parts at each level in nested lists |
| n | the first n elements |
| -n | the last n elements |
| {n} | element n only |
| {m,n} | elements m through n (inclusive) |
| {m,n,s} | elements m through n in steps of s |
| All | all parts |
| None | no parts |
Much like Part, Take and Drop can be viewed as picking out sequences of slices at successive levels in a nested list, you can use Take and Drop to work with blocks of elements in arrays.
| Prepend[list,elem] | add element at the beginning of list |
| Append[list,elem] | add element at the end of list |
| Insert[list,elem,i] | insert element at position i |
| Insert[list,elem,{i,j,…}] | insert at position {i,j,…} |
| Delete[list,i] | delete the element at position i |
| Delete[list,{i,j,…}] | delete at position {i,j,…} |
| ReplacePart[list,i->new] | replace the element at position i in list with new |
| ReplacePart[list,{i,j,…}->new] | replace list[[i,j,…]] with new |
| ReplacePart[list,{i1->new1,i2->new2,…}] | replaces parts at positions in by newn |
| ReplacePart[list,{{i1,j1,…}->new1,…}] | replace parts at positions {in,jn,…} by newn |
| ReplacePart[list,{{i1,j1,…},…}->new] | replace all parts list[[ik,jk,…]] with new |
This replaces the first and fourth parts of the list. Notice the need for double lists in specifying multiple parts to replace:
It is important to understand that ReplacePart always creates a new list. It does not modify a list that has already been assigned to a symbol the way m[[…]]=val does.
| {list1,list2,…} | list of lists |
| Table[expr,{i,m},{j,n},…] | m×n×… table of values of expr |
| Array[f,{m,n,…}] | m×n×… array of values f[i,j,…] |
| Normal[SparseArray[{{i1,j1,…}->v1,…},{m,n,…}]] | |
m×n×… array with element {is,js,…} being vs | |
| Outer[f,list1,list2,…] | generalized outer product with elements combined using f |
| Tuples[list,{m,n,…}] | all possible m×n×… arrays of elements from list |
Functions like Array, SparseArray, and Outer always generate full arrays, in which all sublists at a particular level are the same length.
| Dimensions[list] | the dimensions of a full array |
| ArrayQ[list] | test whether all sublists at a given level are the same length |
| ArrayDepth[list] | the depth to which all sublists are the same length |
The Wolfram Language can handle arbitrary nested lists. There is no need for the lists to form a full array. You can easily generate ragged arrays using Table.
| Flatten[list] | flatten out all levels of list |
| Flatten[list,n] | flatten out the top n levels |
| ArrayFlatten[list,rank] | create a flattened array from an array of arrays |
Flatten in effect puts elements in lexicographic order of their indices:
| Transpose[list] | transpose the top two levels of list |
| Transpose[list,{n1,n2,…}] | put the k th level in list at level nk |
| Map[f,list,{n}] | map f across elements at level n |
| Apply[f,list,{n}] | apply f to the elements at level n |
| MapIndexed[f,list,{n}] | map f onto parts at level n and their indices |
| Partition[list,{n1,n2,…}] | partition into n1×n1×… blocks |
| PadLeft[list,{n1,n2,…}] | pad on the left to make an n1×n1×… array |
| PadRight[list,{n1,n2,…}] | pad on the right to make an n1×n1×… array |
| RotateLeft[list,{n1,n2,…}] | rotate nk places to the left at level k |
| RotateRight[list,{n1,n2,…}] | rotate nk places to the right at level k |
| Partition[list,n] | partition list into sublists of length n |
| Partition[list,n,d] | partition into sublists with offset d |
| Split[list] | split list into runs of identical elements |
| Split[list,test] | split into runs with adjacent elements satisfying test |
Partition in effect goes through a list, grouping successive elements into sublists. By default it does not include any sublists that would "overhang" the original list.
You can tell Partition to include sublists that overhang the ends of the original list. By default, it fills in additional elements by treating the original list as cyclic. It can also treat it as being padded with elements that you specify.
You can think of Partition as extracting sublists by sliding a template along and picking out elements from the original list. You can tell Partition where to start and stop this process.
| Partition[list,n,d] or Partition[list,n,d,{1,-1}] | keep only sublists with no overhangs |
| Partition[list,n,d,{1,1}] | allow an overhang at the end |
| Partition[list,n,d,{-1,-1}] | allow an overhang at the beginning |
| Partition[list,n,d,{-1,1}] | allow overhangs at both the beginning and end |
| Partition[list,n,d,{kL,kR}] | specify alignments of first and last sublists |
| Partition[list,n,d,spec] | pad by cyclically repeating elements in list |
| Partition[list,n,d,spec,x] | pad by repeating the element x |
| Partition[list,n,d,spec,{x1,x2,…}] | |
pad by cyclically repeating the xi | |
| Partition[list,n,d,spec,{}] | use no padding |
An alignment specification {kL,kR} tells Partition to give the sequence of sublists in which the first element of the original list appears at position 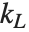 in the first sublist, and the last element of the original list appears at position
in the first sublist, and the last element of the original list appears at position 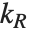 in the last sublist.
in the last sublist.
In some cases it may be convenient to insert explicit padding into a list. You can do this using PadLeft and PadRight.
| PadLeft[list,n] | pad to length n by inserting zeros on the left |
| PadLeft[list,n,x] | pad by repeating the element x |
| PadLeft[list,n,{x1,x2,…}] | pad by cyclically repeating the xi |
| PadLeft[list,n,list] | pad by cyclically repeating list |
| PadLeft[list,n,padding,m] | leave a margin of m elements on the right |
| PadRight[list,n] | pad by inserting zeros on the right |
If you give a nested list as a padding specification, its elements are picked up cyclically at each level.
Lists are normally specified in the Wolfram Language just by giving explicit lists of their elements. But particularly in working with large arrays, it is often useful instead to be able to say what the values of elements are only at certain positions, with all other elements taken to have a default value, usually zero. You can do this in the Wolfram System using SparseArray objects.
| {e1,e2,…}
,
{{e11,e12,…},…}
,
… | ordinary lists |
| SparseArray[{pos1->val1,pos2->val2,…}] | |
sparse arrays | |
| SparseArray[list] | sparse array version of list |
| SparseArray[{pos1->val1,pos2->val2,…}] | |
sparse array with values vali at positions posi | |
| SparseArray[{pos1,pos2,…}->{val1,val2,…}] | |
the same sparse array | |
| SparseArray[Band[{i,j}]->val] | banded sparse array with values val |
| SparseArray[data,{d1,d2,…}] | d1×d2×… sparse array |
| SparseArray[data,dims,val] | sparse array with default value val |
| Normal[array] | ordinary list version of array |
| ArrayRules[array] | position-value rules for array |
An important feature of SparseArray is that the positions you specify can be patterns.
You can think of SparseArray[rules] as taking all possible position specifications, then applying rules to determine values in each case. As usual, rules given earlier in the list will be tried first.
For many purposes, the Wolfram System treats SparseArray objects just like the ordinary lists to which they correspond. Thus, for example, if you ask for parts of a sparse array object, the Wolfram System will operate as if you had asked for parts in the corresponding ordinary list.
Many operations treat SparseArray objects just like ordinary lists. When possible, they give sparse arrays as results.
Dot works directly with sparse array objects:
The Wolfram System represents sparse arrays as expressions with head SparseArray. Whenever a sparse array is evaluated, it is automatically converted to an optimized standard form with structure SparseArray[Automatic,dims,val,…].
This structure is, however, rarely evident, since even operations like Length are set up to give results for the corresponding ordinary list, not for the raw SparseArray expression structure.
Length gives the length of the corresponding ordinary list:
Map also operates on individual values: