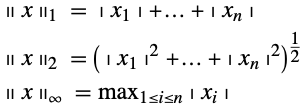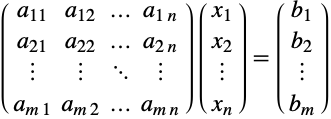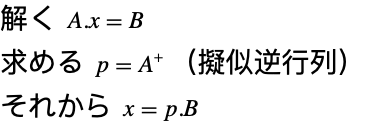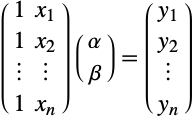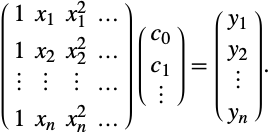最新のWolfram言語には，このチュートリアルに関連する新機能が追加されている．最新情報は行列と線形代数を参照のこと．

行列の計算

基本操作	固有空間の計算
線形系の解法	行列の分解
最小二乗法	行列の関数

このチュートリアルでは，行列の計算を実行するためのWolfram言語関数について述べる．これらの関数についての詳細はGolub，van LoanやMeyerらの標準的な数学の教科書を参照していただきたい．このチュートリアルで取り上げる操作は行列に特有のものである．しかしノルムの計算については例外で，スカラーとベクトルにも使用できる．

基本操作

このセクションでは，このチュートリアルで行列の操作について述べる際に使用する基本的な概念と操作についてまとめる．

ノルム

数学的オブジェクトのノルムはオブジェクトの長さ，サイズ，範囲の計測である．Wolfram言語では，ノルムはスカラー，ベクトル，行列について求められる．

Norm[num]	数のノルム
Norm[vec]	ベクトルの2‐ノルム
Norm[vec,p]	ベクトルの p‐ノルム
Norm[mat]	行列の2‐ノルム
Norm[mat,p]	行列の p‐ノルム
Norm[mat,"Frobenius"]	行列のフロベニウス(Frobenius)ノルム

Wolfram言語におけるノルムの計算

数値のノルムは絶対値となる：

ベクトルのノルム

ベクトル空間では，ノルムで距離が計算できる．これにより，近傍，近似の近さ，フィットの良さ等の多くの身近な概念が定義できるようになる．ベクトルノルムは以下の関係を満たす関数である．

一般にこの関数にはという表記を用いる．下付き文字はノルムの識別に使われる．その中でも特に p-ノルムは重要である．p-ノルムはについて以下のように定義される．

よく使われる p-ノルムには1-，2-，-ノルムがある．

Wolfram言語では，ベクトルの p-ノルムの計算には関数Normを使う．例として，以下で1-，2-，

-ノルムを求める：

2-ノルムはデフォルトであり，特に有用である：

ノルムは厳密数のベクトルについて実装されている：

ノルムはベクトルに対して，記号的なものとしても組み込まれている：

また，記号 p が使われると，結果も記号的なものとなる：

行列のノルム

行列空間において行列のノルムは距離の測定に使われる．これはある行列が他の行列に近い場合，例えば行列がほぼ特異行列であるということの意味を定量化する場合に必要である．

行列ノルムには2重線を使ったベクトルノルムの表記も使える．最も一般的なノルムのひとつにフロベニウスノルムがある．これはユークリッド(Euclidean)ノルムとも呼ばれる．

この他に一般的なノルムとして p-ノルムがある．p-ノルムはベクトルのp-ノルムに基づいて以下のように定義されている．

従って，行列の p-ノルムはどのベクトルについても適用できるように最大限拡張できる．

Wolfram言語では，フロベニウスノルムは以下のようにして計算できる：

行列の2-ノルムは次のように計算できる：

1，2，

のそれぞれの行列p-ノルムを指定するために引数を渡すこともできる：

次の式は，異なるベクトルに対して，行列のノルムの定義式に沿った入力行列のノルムに準ずる値を計算する．最大値でも2-ノルムより小さいことが分かる：

p-ノルムはすべて，厳密数の行列についてサポートされている：

しかし，1および

の行列に限り，p-ノルムは記号行列についてサポートされている：

NullSpace

各行列に関連付けられている基本的な部分空間に零空間がある．行列の零空間のベクトルは行列による一次変換でゼロベクトルとなる．

NullSpace[m]

1次結合が

を満たす基底ベクトルのリスト

非特異正方行列等，行列によっては零空間が空であることがある：

次の行列は1つのベクトルで生成される零空間を持つ

次の行列は基底ベクトル2つと零空間を持つ：

階数

行列の階数は行列中で線形独立な行または列の数を表す．

MatrixRank[mat]

行列 mat の階数

m×n の行列に互いに線形従属な行が存在しない場合，その行列の階数は

である．また，この行列は最大階数(full rank)行列と呼ばれる：

行列の中に互いに従属な行が含まれる場合は，その行列の回数は

より小さくなる．この場合，この行列は階数落ち(rank deficient)であるという：

行列の階数はその転置行列の階数と等しい．これは線形独立である行の数が線形独立である列の数に等しいことを表している：

m×n の行列 A について，Length[NullSpace[A]]+ MatrixRank[A]n およびLength[NullSpace[A^T]]+ MatrixRank[A^T]m が成立する．このことから，階数が n の場合かつその場合に限り，零空間は空であり，A の階数がm の場合かつその場合に限り，A の転置の零空間は空であることが分かる．

階数が列数に等しい場合，この行列は列最大階数であるといわれる．階数が行数に等しい場合は，この行列は行最大階数であるといわれる．行列の階数を理解するには，行の階段形を考えるとよい．

被約階段行列

行列は，最も左上の要素のピボット位置から始めて，ピボット行の倍数を後続の行から引き，ピボット列のピボットより下の要素がすべてゼロになるようにする操作の組合せで，行の階段形へ変換することができる．次のピボットは次の行および列に移動して選ばれる．このピボットがゼロであり，かつその下の列に非零の要素がある場合は，行を入れ換えて操作を繰り返す．この操作を最終行および最終列に至るまで繰り返す．

要素がすべてゼロである行の下の行も要素がすべてゼロである行のみであるか，または番目の行の最初の非零要素が番目の列にあり，番目の列の最初から番目までの要素がゼロの場合は，その行列は行階段行列であるという．被約階段形はひとつではないが，その形（ピボットの位置という意味で）はひとつである．非零の行の数で行列の階数を求めることもできる．

行列が行階段形であり，各ピボットが1で，その上（および下）の要素がすべてゼロなら，その行列は被約階段行列である．これは行階段行列と同様の方法で，ピボットを除算により1にし，現在のピボット行の倍数を引くことでその行のピボットより上の要素をゼロにする操作を行うことで生成できる．

被約階段形（および行階段形）により，非零の行の数で行列の階数を求めることができる．Wolfram言語では被約階段行列は関数RowReduceで計算できる．

RowReduce[mat]

行列 mat の被約階段形

次の行列の被約階段形の非零行は1行だけである．このことから，この行列の階数は1であることがわかる：

次は3×2の乱数行列であり，各行は線形独立である：

被約階段行列には非零行が2行あるので，階数は2である：

MatrixRankで求めた階数も2である：

転置行列の被約階段形にも非零行が2行ある．これは行列の階数がその転置行列の階数と等しいということと一致している．これは行列が長方行列であった場合についても同じである：

逆行列

正方行列 A の逆行列は次のように定義されている．

ここでは単位行列である．Wolfram言語では逆行列は関数Inverseを使って求めることができる．

Inverse[mat]

行列 mat の逆行列

2×2行列の例である：

行列が定義を満足することを示す：

逆行列の存在しない行列もある．このような行列を特異行列という．行列が階数落ちなら，その行列は特異行列である：

逆行列は原則として行列方程式の解法に用いることができる．

この場合，の逆行列を掛け合せることで解が求められる．

しかし，どのような行列方程式も直接解く方がよい．直接解く方法については「線形系の解法」のセクションで述べる．

擬似逆行列

行列が特異行列である場合，または正方行列でない場合でも，を最小にする近似の逆行列を求めることはできる．2-ノルムを使う場合は，最小二乗法で擬似逆行列を求める．

PseudoInverse[mat]

行列 mat の擬似逆行列を求める

次の式は上で定義した特異行列の擬似逆行列を求める：

結果は単位行列ではないが，単位行列に「近い」ものとなる：

長方行列の擬似逆行列を求める：

次の結果は単位行列に極めて近い：

擬似逆行列で求める解は最小二乗解である．これについては「最小二乗法」のセクションで詳しく述べる．

行列式

n×n 行列の行列式は次のように定義されている．

これはWolfram言語では関数Detを使って計算できる．

Det[mat]	行列 mat の行列式
Minors[mat]	mat の小行列式の行列
Minors[mat,k]	mat の k 番目の小行列式

2×2行列の例である：

行列式の便利な性質に，

が特異行列である場合かつその場合に限り，

であるということがある：

上記のように，特異行列は最大階数を持たない：

小行列式

行列の小行列式は，その行列の任意の k×k 部分行列の行列式である．次の例ではすべての2×2小行列式を求めるのに関数Minorsを使う：

部分行列の大きさは第2引数で指定する．次の式では1×1の小行列式を計算する．つまりこれは行列の要素である：

Minors[m]とMinors[m,n-1]は等しい．一般にMinors[m,k]では，行列 m から異なる k 行と k 列を取り出して生成される，可能なすべてのk×k 部分行列の行列式が計算される．4×4行列の2×2小行列式については，4行から2行，4列から2列を取り出す方法はそれぞれ6通りのみであるので，6×6行列を得る：

行列の階数の性質のひとつに，最大の非特異部分行列の大きさに等しいということがある．これはMinorsで示すことができる．次の例において，行列の階数は2である：

行列式はゼロである：

2×2小行列式を計算すると，階数は2であり，すべてがゼロである訳ではないことが分かる：

線形系の解法

行列の重要な使用法のひとつに，線形系の表現と解法が挙げられる．このセクションではWolfram言語で線形系をどのように解くかについて述べる．ここでは特にこの目的で提供されている主な関数LinearSolveを使う．

線形系の解法では，行列方程式を解く．は × の行列なので，個の未知数を含む個の線形方程式である．

のとき，系は正方であるという．の場合は未知数より方程式の数の方が多く，過剰決定系である．のときは未知数の方が方程式の数より多く，過少決定系である．

square	m=n の場合．解は存在することもしないこともある
overdetermined	m>n の場合．解は存在することもしないこともある
underdetermined	m<n の場合．解は存在しないか，あるいは無限個の解が存在する
nonsingular	独立した方程式の数と変数の数が等しく，行列式が非零の場合．唯一解が存在する
consistent	少なくとも解が1つ存在する
inconsistent	解は存在しない

長方行列で表せる線形系の種類

で逆行列を計算して行列方程式を解くことができるとしても，それは推奨される方法ではない．線形系を直接解くように設計されている関数を使うべきである．Wolfram言語ではLinearSolveが使用できる．

LinearSolve[m,b]	行列方程式 m.x==b の解のベクトル x
LinearSolve[m]	多くのb に繰返し適用できる関数

LinearSolveを使った線形系の解法

LinearSolveを使用して行列方程式を解く：

得られた解が，問題の解となっているかどうかを確かめることもできる：

線形方程式はどのような入力行列からでも生成できる：

その後で，Solveを使って解を求めることもできる：

LinearSolveは行列方程式の右辺が行列の場合でも使用できる：

過剰決定系の場合，LinearSolveは解が存在するなら求める：

解が見つからない場合は，系は矛盾している．この場合，最も近い解を求めるとよいこともある．これは多くの場合最小二乗法を使って行う．これについては「最小二乗法」で述べる．

過少決定系の場合は解は存在しないか，無限に存在する．後者の場合はLinearSolveは解を1つだけ返す：

行列

の階数が，

に追加列として

を加えた行列（拡大行列）の階数と等しい場合は，系は整合（少なくとも1つの解を持つ）している．次の例では前述の系が整合していることを示す：

LinearSolveはWolfram言語がサポートしているすべてのタイプの行列について使用できる．このような行列には記号的および厳密な数，機械数，任意精度数の行列が含まれる．また，密行列と疎行列のどちらにでも使える．LinearSolveで疎行列を使用する際は，疎行列に適した方法が適用され，結果は解のベクトルとなる：

オプション名	デフォルト値
Method	Automatic	解法に使用するメソッド
Modulus	0	方程式を n を法とするものとする
ZeroTest	(#0&)	ゼロであるかどうかのテストで記号的メソッドに使用する関数

LinearSolveのオプション

LinearSolveにはユーザがより細かくコントロールするための3つのオプションがある．オプションModulusおよびZeroTestは記号的な方法に適用できる．これらについては「記号的行列および厳密行列」のセクションで述べる．オプションMethodを使うと，特定の問題に適していることが知られているメソッドを指定することができる．デフォルトの設定はAutomaticで，LinearSolveは入力に基づいてメソッドを選択する．

特異行列

逆行列が存在しない行列は特異行列と呼ばれる．特異行列であるかどうかを判断する方法のひとつは，行列式を計算することである．特異行列の行列式はゼロとなる：

多くの右辺の値には解が存在しない：

しかし，ある特定の値には解が存在する：

最初の例では，

の階数は拡大行列の階数と等しくなかった．次の式では，系が矛盾しており，LinearSolveで解くことができないことを示す：

2つ目の例では，

の階数は拡大行列の階数と等しかった．次の式では，系が整合しており，LinearSolveを使って解けることを示す：

解が見つからない場合でも，問題に最も適した解を求めることはできる．最も近い解のうち，重要なもののひとつに，最小二乗法を使うものがある．これについては「最小二乗法」に記述されている．

同次方程式

同次行列方程式の右辺はゼロである．

この方程式は，行列が特異行列の場合は非零の解を持つ．行列が特異であるかどうかは，行列式を計算して確認できる．

同次方程式の解は，関数NullSpaceを使って求められる．NullSpaceは直交ベクトル一式を返す．その各々が同次方程式の解である．次の例ではベクトルは1つのみである：

解が実際に同次方程式を満足することを示す：

関数Chopは近似値を0に置き換えるときに使える：

同次方程式の解は，非同次方程式の一般解を形成するときに使える．次の式は非同次方程式の解である：

解は実際に方程式を満足する：

同次方程式の解にsolの任意数倍を加算した結果のベクトルも行列方程式の解である：

精度の推定と計算

線形系の解の精度を求める重要な方法のひとつに，条件数を求めるというものがある．これは各ノルムについて次のように定義されている．

行列方程式について，の相対誤差はとの相対誤差の倍である．そのため，条件数が解の精度を表すのである．行列の条件数が大きければ，その行列は悪条件であるという．悪条件の系からは良い解は得られない．非常に悪条件の系からは解は全く得られない．

Wolfram言語では，関数LinearAlgebra`MatrixConditionNumberを使って条件数の近似を計算する．

LinearAlgebra`MatrixConditionNumber[mat]
	近似数行列の無限大ノルム近似条件数
LinearAlgebra`MatrixConditionNumber[mat,Norm->p]
	行列の p‐ノルム近似条件数（p は1，2，のいずれか）

行列の条件数を計算する：

次の行列は特異行列で，条件数は

である：

次の行列の条件数は大きく，悪条件である：

ある行列に同じ行列を掛け合せると，条件数は増加する：

悪条件の行列を含む行列方程式を解く場合，結果が正確ではないこともある：

行列mat2についての解の精度はより低い：

この問題を解決する方法としては，悪条件となる可能性のある行列ができないようにする，つまり行列にそれ自身を掛け合せることを避ける等が挙げられる．この他に，Wolfram言語の任意精度計算を使ってもよい．これについては「任意精度行列」で述べる：

記号行列および厳密行列

LinearSolveはWolfram言語で表現できるすべての行列の型について使用できる．詳細は「行列の型」で述べる．ここでは純記号行列についての例を示す．

これは純粋に記号的な行列を扱う例である：

もとの行列を解に掛け合せる：

掛け算の結果を希望の値にするには，Simplifyを使った後処理が必要である．次の例では，記号線形代数計算において中間処理が必要であることを示す．処理を行わないと中間結果が非常に大きくなり，計算スピードが遅くなってしまう可能性がある：

中間式を簡約する際，ZeroTestオプションが便利であることがある．

LinearSolveも厳密問題の解法に使える：

記号計算あるいは厳密計算に特化した方法はCofactorExpansion，DivisionFreeRowReduction，OneStepRowReduction等数多く存在する．詳細は「記号法」で述べる．

行の削減

行の削減は，可能ならゼロになるように行の倍数を加えることで行う．結果の行列は前述のように行階段行列となる．入力行列が非特異行列の場合は，結果は単位行列となる：

方程式の系を解くことができる：

これはLinearSolveを以下のように使っても計算できる：

行列の分解の保存

線形方程式系を扱う分野では，同じ行列

に対して，さまざまな右辺

を与えることが多い．系の解法における労力の多くは

の処理に費やされるため，結果として得られる行列 A の分解を保存し，繰り返し問題を解く際に使用するのが一般的である．Wolfram言語では，LinearSolveに引数を1つ適用することで，行列の分解を保存する関数が返され，さまざまなベクトルを適用して各解を得ることができる：

LinearSolveFunctionを特定の右辺に適用すると，解が得られる：

この解は行列方程式を満足する：

右辺が異なると，解も異なる：

新しい解も行列方程式を満足する：

LinearSolveに引数を1つだけ適用する場合でも，2つ適用する場合と全く同じである．対応している入力行列も同じであり，例えば記号，厳密，疎行列の入力について期待どおりの結果を返す．同じオプションも使用できる．

引数を1つのみ適用する際の問題点のひとつに，ある特定の入力行列については行列の分解が保存できないことが挙げられる．例えば系が過剰決定系の場合，厳密解が存在するかどうかは定かではない．この場合，その右辺については関数が適用されるたびに行列の分解が繰り返されるという警告メッセージが現れる：

次の右辺に対して解が存在するので，次のような解が返される：

しかし，次の右辺については解が存在しないので，エラーが生じる：

メソッド

LinearSolveには行列方程式を解くための，それぞれ特有の問題に特化したさまざまな方法が実装されている．オプションMethodを使うと，その方法を指定することができる．このように，Wolfram言語では，行列方程式を解くための機能がすべて1つのインターフェースに集約されている．

オプションMethodのデフォルトの設定はAutomaticである．これはWolfram言語で頻繁に見かける設定であり，どのメソッドを使うかをシステムが自動的に決めるということを意味する．LinearSolveについては，入力行列が数値かつ密であるなら，LAPACKルーチンを使う解法使われる．数値かつ疎である場合は，マルチフロンタル直接解法が使われる．行列が記号的な場合は，記号計算専用ルーチンが使われる．

以下に各種メソッドの詳細を述べる．

LAPACK

LAPACKは数値密行列の解法においてデフォルトのメソッドである．行列が正方行列かつ非特異の場合，実行列にはdgesv，dlange，dgeconルーチンが，複素数行列にはzgesv，zlange，zgeconルーチンが使われる．行列が正方行列ではない場合，または特異行列の場合は，実行列にはdgelss，複素数行列にはzgelssが使われる．LAPACKについての詳細は参考文献を参照のこと．

入力行列が任意精度数を使用している場合，LAPACKアルゴリズムは任意精度計算に拡張して使用される．

マルチフロンタル

マルチフロンタル法は，入力行列が疎行列の場合にデフォルトとなる直接解法である．これはMethodオプションで指定することもできる．

次の式はMatrix Market形式の疎行列の例を読み込む．行列のインポートに関する詳細は「疎行列のインポートとエキスポート」を参照のこと：

読み込んだ行列に関する行列方程式を解く：

マルチフロンタル法に対する入力行列が密行列の場合，入力行列は疎行列に変換される．

マルチフロンタル法の実装は"UMFPACK"ライブラリを使用している．

クリロフ(Krylov)

クリロフ法は，偏微分方程式の数値的な解法で生じる系等，大規模で疎な線形系に適した反復解法である．Wolfram言語には2つのクリロフ法が実装されている．ひとつは対称正定値行列用の共役勾配法，もうひとつは非対称系用のBiCGSTAB（安定化双共役勾配法）である．適切なサブオプションを使うと，使われるメソッドと，その他の数多くのパラメータを設定することができる．

オプション名	デフォルト値
MaxIterations	Automatic	最大反復回数
Method	BiCGSTAB	解法に使用するメソッド
Preconditioner	None	前処理
ResidualNormFunction	Automatic	最小化するノルム
Tolerance	Automatic	反復の中止に使用する許容範\ 囲

クリロフ法のサブオプション

クリロフ法のデフォルトのメソッドBiCGSTABはよりコストが高いが，多くの場合に効果的である．もう一方のメソッドである共役勾配法は対称正定値行列に適しており，解は常に収束する（収束速度が遅いこともある）．行列が対称正定値行列でない場合，共役勾配法の解は収束しないこともある．

次の例では，行列は対称正定値行列ではなく，解が収束しない：

デフォルトのメソッドBiCGSTABは収束し，解を返す：

求められた解を検証する：

次の例ではクリロフ法の利点と前処理方法を示す．まず，ある構造を入れた帯行列を作る関数を定義する：

この関数で生成された行列の構造を見てみる：

次はより大きい10000×10000の行列を作成する：

疎行列に対しては，デフォルトでマルチフロンタル直接解法が使用される：

クリロフ法の方が早い：

ILU前処理を行うと，さらに早くなる．現在のところ，行列が非零の対角要素を持つ場合に限り前処理が行える：

現時点で組み込まれているのはILU前処理のみである．しかし，入力行列に適用する関数を定義して，新たな前処理を定義することもできる．次の例では対角行列の解を求める．

まず問題を設定し，前処理なしで解く：

次に前処理関数funを使う．計算速度が顕著に上がる：

一般に，この手の単純な前処理で効果があるような構造を持つ問題はないだろう．しかしこの例は，独自の前処理を作って使用する方法を示しているため，役立つだろう．

クリロフ法の入力行列が密の場合でも，このメソッドは行列/ベクトル操作に基づいているため，解を求めることができる．

クリロフ法は直接法には大きすぎる系にでも使用できる．しかし，これは一般的な解法ではなく，特に対角優勢の形の問題に適している．

コレスキー(Cholesky)

コレスキー法は対称正定値系の解法に適している：

コレスキー法は次の行列については早い：

コレスキー法はより安定している．次の行列でそれを例示する：

この行列については，デフォルトのLU分解法では潜在的なエラーが指摘される：

コレスキー法では正常に計算できる：

コレスキー法を密行列に適用する際，実行列についてはdpotrfやdpotrs，複素数行列についてはzpotrf，zpotrs等のLAPACK関数が使われる．疎行列の場合，コレスキー法は"TAUCS"ライブラリを使う．

記号的メソッド

記号計算および厳密計算に適した方法もCofactorExpansion，DivisionFreeRowReduction，OneStepRowReductionのようにたくさんある．これらを以下の記号行列で例示する：

計算を3種類のメソッドで繰り返す：

最小二乗法

このセクションは，行列方程式

の解を求める前セクションからの続きである．ここで

は

の行列であり，

（未知数の数より方程式の数の方が多い）である．この場合，解がないことが多く，LinearSolveは警告メッセージを表示する：

このような場合，を最小にする最も近い解を求めることができる．p は2にするのが特に一般的である．これにより最小二乗解が得られる．関数はで微分可能であり，また2-ノルムは直行変換でもそのまま維持されるため，これらは頻繁に使われる．

の階数が（列最大階数）の場合，最小二乗法問題に唯一解が存在（Golub，van Loan）し，それが次の線形系の解であることが示されている．

これは正規方程式と呼ばれる．この方程式を直接解いて最小二乗解を得ることもできるが，お勧めしない．なぜなら行列が悪条件の場合に積はさらに悪条件になるからである．最大階数行列の最小二乗解を求める方法については，「例題：最大階数最小二乗解」で詳しく探求する．

その他のノルム，例えば1やのノルムを最小にする近似解を求めることも可能である．「1-ノルムと無限ノルムの最小化」において，特定のタイプの行列に適した，あるいは他のノルムを最小にする過剰決定系の解を求める多くの方法について述べる．

過剰決定系の最小二乗解を求める一般的な方法として，特異値分解を用いて擬似逆行列といわれる行列を作るということが挙げられる．Wolfram言語ではPseudoInverseを使って計算する．この方法は，階数落ちの入力行列についても使える．以下にその基本的な方法を示す．

以下は過剰決定系である．行列

は階数落ちであることが分かる：

PseudoInverseを使って最小二乗解を求めることはできる：

実際に解がどのくらい近いかを示す：

データフィット

科学計測の結果の多くはデータの順序対ある．計測されていない部分の予測をするためには，曲線をデータ点にフィットするのが一般的である．曲線が直線の場合は，すべてのデータについて，以下の未知の係数，を求めることになる．

これは以下のように行列形式で表すことができ，線形系の過剰決定系の解法と等しいことが即座に分かる．

例えば，より一般的な曲線

にフィットすることは，以下の行列方程式と同等である．

この場合，左辺の行列はヴァンデルモンド(Vandermonde)行列である．実際，係数は未知でも線形の関数なら，どのようなものでも使える．

最もフィットするパラメータの求め方の例を示す．以下のような計測から始める：

これらのデータをプロットする：

「擬似逆行列」で述べられているPseudoInverseを使ってこの問題を解いてみる．まず，データを

，

要素に分割する：

行列の左辺を形成する：

最もフィットするパラメータは次のようにして求められる：

Wolfram言語には関数FindFitがあり，これを使ってデータに最もフィットする解が求められる．この場合の解は，PseudoInverseを使った場合の解と一致する：

最後に，データ点とそれにフィットする曲線をプロットする：

関数FindFitは非常に一般的である．例えば，パラメータによっては線形でないデータにフィットすることもできる．

固有空間の計算

固有値問題の解法は，行列計算の主要分野のひとつであり，物理，化学，工学に広く応用されている．× 行列の固有値は，固有多項式の個の根である．根は行列のスペクトルと呼ばれる．各固有値について

を満たすベクトルを固有ベクトルという．固有ベクトルから成る行列が存在し，これが非特異の場合，対角要素に固有値を持つ対角行列を作るための相似変換に使うことができる．固有値の重要な応用分野の多くにおいて，このような行列の対角化が必要となる．

Wolfram言語には，固有値と固有ベクトルを計算するためのさまざまな関数がある．

Eigenvalues[m]	m の固有値のリスト
Eigenvectors[m]	m の固有ベクトルのリスト
Eigensystem[m]	{eigenvalues,eigenvectors}という形式のリスト
CharacteristicPolynomial[m,x]	m の固有多項式

固有値と固有ベクトル

2×2行列の例：

固有値を計算する：

固有ベクトルを計算する：

Eigensystemを使うと，固有値と固有ベクトルの両方を計算することができる：

最初の固有値とその固有ベクトルが定義を満足することを確認する：

EigenvectorsとEigensystemは固有ベクトルのリストを返す．列が固有ベクトルである行列が必要な場合は転置しなければならない．以下に固有値と，対応する固有ベクトルが固有ベクトルの定義を満たしていることを示す：

行列の固有多項式も求められる：

固有多項式の根を求める．行列の固有値と一致しているように見える：

固有値の計算は密行列だけでなく，疎行列にも適用できる．次の例では，固有値の1つはゼロである：

固有値がゼロというのは，行列の零空間が空ではないことを意味している：

固有値の応用分野によっては，すべての固有値が必要な訳ではないこともある．Wolfram言語には固有値を一部だけ計算する方法もある．

Eigenvalues[m,k]	m の固有値の大きい方からk 個
Eigenvectors[m,k]	m の対応する固有ベクトル
Eigenvalues[m,-k]	m の固有値の小さい方からk 個
Eigenvectors[m,-k]	m の対応する固有ベクトル

次の例は行列が非常に大規模なときに特に便利である．10000×10000の疎行列を考える：

最大の固有値を求める：

オプション名	デフォルト値
Cubics	False	3×3の行列の場合に根号を使って表現する
Method	Automatic	解法に使用するメソッド
Quartics	False	4×4の行列の場合に根号を使って表現する
ZeroTest	(#0&)	ゼロであるかどうかテストする記号的メソッドで使用する関数

Eigensystemのオプション

Eigensystemは4種類のオプションを使ってより詳細な調整ができるようになっている．オプションCubics，Quartics，ZeroTestは記号的な手法のときに用いる．これについては「記号行列と厳密行列」で述べる．オプションMethodは上級ユーザが問題に特に適しているメソッドを指定するためのものである．このオプションのデフォルトの設定はAutomaticで，一般に適していると考えられるメソッドがEigensystemによって自動的に選ばれる．

固有空間の特性

このセクションでは，固有空間の計算に特有の特性について述べる．× 行列の固有値は次多項式の根に関連付けられるため，常に個の固有値が存在する．

行列が含んでいるのが実数のみであっても，その固有値が実数であるとは限らない：

行列の固有値は重複することがある．重複しない固有値は単純であるという．次の例では，重複する固有値は重複する数だけ固有ベクトルを持つ．この場合は半単純であるという：

重複する固有値の重複度より固有ベクトルの数の方が少ないことがある．このような固有地は不完全(defective)であるといい，行列も不完全な行列といわれる：

行列の固有値にゼロが含まれても，固有値の個数分の固有ベクトルを持つ場合もある：

行列の固有値にゼロが含まれ，固有値の個数分の固有ベクトルを持たない場合もある：

行列が実対称行列の場合，すべての固有値は実数となり，固有ベクトルの正規直交基底が存在する：

固有ベクトルは正規直交基底である：

正の固有値を持つ実対称行列は正定値行列という：

非零の固有値をもつ実対称行列は半正定値行列という：

行列が複素エルミート行列（自身の共役転置に等しい行列）の場合，固有値はすべて実数で，固有ベクトルの正規直交基底が存在する：

固有ベクトルは正規直交基底である：

正の固有値を持つエルミート行列は正定値行列という：

行列の対角化

固有空間計算の利用法のひとつに，行列を対角化する相似変換を行うということがある：

行列の相似変換を行っても，行列の有用な性質の値，つまり行列式，階数，固有和等は変化しない．

行列の固有ベクトルが特異であると，その行列は対角化できない．これは行列が不完全（完全な固有ベクトル一式を持たない固有値がある）な場合に生じる．以下にその例を示す：

行固有ベクトルの行列は特異であり，もとの行列を対角化する相似変換は存在しない：

記号行列と厳密行列

記号あるいは厳密行列についての計算が終ると，Wolfram言語は通常の計算と同様に，記号計算代数技術を使って記号解また厳密解を返す．

3×3の整数行列の例である：

固有値を計算する．結果にはRootオブジェクトが使われる：

Nを使って，結果を機械精度で近似する：

CubicsオプションをTrueと設定すると，根号を使った結果が得られる：

一般化された固有値

× 行列について，一般化された固有値はその固有多項式の個の根である．一般化された各固有値について，

を満たすベクトルを一般化された固有ベクトルという．

Eigenvalues[{a,b}]	a と b の一般化された固有値
Eigenvectors[{a,b}]	a と b の一般化された固有ベクトル
Eigensystem[{a,b}]	a と b の一般化された固有空間

一般化された固有値と固有ベクトル

2つの2×2行列がある：

一般化された固有値を計算する：

2つの行列が同じ非零の零空間を共有しているなら，確定できない固有値が存在する：

次の2つの行列は，同じ1次元零空間を共有している：

一般化された固有値のひとつはIndeterminateである：

メソッド

固有値の計算は特定の問題に特化したいくつもの方法を使って行われる．オプションMethodを使うとその方法が選べる．このようにしてWolfram言語の持つすべての機能が1つのインターフェースですべて使える．

オプションMethodのデフォルトの設定はAutomaticである．これは一般に，Wolfram言語ではシステムがどのメソッドを使うかを自動的に決めるということである．固有値の計算については，入力が × の機械数行列で，必要とされる固有値の数がの20%より小さいならば，アーノルディ(Arnoldi)法が使われる．それ以外の場合で，入力行列が数値的なら，LAPACKルーチンを使うメソッドが使われる．記号行列の場合は，記号計算専用ルーチンが使われる．

以下に各種メソッドの詳細を述べる．

LAPACK

LAPACKは固有値と固有ベクトルを求める際のデフォルトのメソッドである．行列が非対称の場合，実行列にはdgeevが，複素数行列にはzgeevが使われる．対称行列の場合は，実行列にはdsyevr，複素数行列にはzheevrが使われる．一般化された固有値を求める際は，実行列にはdggevが，複素数行列にはzggevが使われる．LAPACKについての詳細は参考文献を参照のこと．

対称行列の固有値の場合は，Wolfram言語が自動的に適切なメソッドに切り替えるため，計算が速くなる：

入力行列が任意精度数を使用している場合，LAPACKアルゴリズムは任意精度計算に拡張して使用される．

アーノルディ

アーノルディメソッドは，有限個の固有値の計算に使われるインタラクティブなメソッドである．アーノルディメソッドの実装は"ARPACK"ライブラリを使用する．この方法で解くことのできる最も一般的な問題として，以下の固有値を，一部選択したものだけ計算するというものが挙げられる．

これはインタラクティブであり，固有値の一部のみの計算なので，疎行列に適していることが多い．このメソッドの利点のひとつに，シフトを適用して指定の固有ベクトルと固有値 ()について解けるということがある．

これはに近い固有値を求める際に有効である．

アーノルディメソッドには以下のサブオプションが使える．

オプション名	デフォルト値
BasisSize	Automatic	アーノルディ基底の大きさ
Criteria	Magnitude	解法に用いるメソッド
MaxIterations	Automatic	最大反復回数
Shift	None	アーノルディシフト
StartingVector	Automatic	使用する初期ベクトル
Tolerance	Automatic	反復の中止に用いる許容範囲

アーノルディメソッドのサブオプション

3×3の疎行列がある：

アーノルディメソッドを使って最大の固有値を求める：

-1に近い固有値を求める：

固有値と同じ値をシフトに指定すると，エラーが生じることがある：

2対角要素が2でそれ以外が-1である，1500×1500の3重対角行列の固有値を求める．アルゴリズムは収束しない：

収束しない場合でも結果は返されるが，あまり正確でないことがある．収束を促進するために，シフトで得られた結果を使う：

この他に，繰返し回数を増やしても収束が促される：

または，繰返しの回数に加えてアーノルディの基底の大きさを増やしても収束が促進されることがある．この例では，基底サイズを増やすと繰返しの回数が少なくても収束する．各繰返しは高くつくが，全体の計算は速くなる：

アーノルディのアルゴリズムで基底サイズを30としても，密固有値計算と比べて速くて，メモリ使用量も少ないことが多い（計算速度はマシンによって異なる）：

現実の計算で発生する，より大規模である疎な系の多くについても，アーノルディのアルゴリズムは極めて素早く収束できる．

記号的メソッド

記号的な固有値計算は固有多項式を補間して行われる．

行列の分解

このセクションでは，種々の基本的な行列の操作方法について述べる．これらは行列問題の解を求める際のブロックの形成によく使われる．分解は因数分解，直交変換，相似変換に分類される．

LU分解

行列のLU分解は，行列方程式を解く際にガウスの消去法の一環として頻繁に使われる．「線形系の解法」で述べたように，Wolfram言語ではLinearSolveがこれを行うため，行列方程式の解法にLU分解を使う必要がない．同じ左辺が使えるように行列の分解を保存したい場合は，LinearSolveに引数を1つ渡して使用すればよい．これについては「行列の分解の保存」で例を示した．

正方非特異行列をピボットを部分選択してLU分解するときは，以下を満たす一意的な行列，，を使う．

ここで，は対角を含む下三角，は上三角，は置換行列である．これが求まったら，次の等価系の解を求めることで，行列方程式を解くことができる．

まず次の式でについて解く．

次にについて解いて希望の解を得る．

もも三角行列なので，これらの系は容易に解ける．

Wolfram言語では行列方程式の解法にLU分解を必要としないが，Wolfram言語にはLU分解の計算のための関数LUDecompositionがある．

LUDecomposition[m]

部分ピボットを利用したLU分解

LUDecompositionは3要素のリストを返す．1つ目の要素は上・下三角行列の組合せ，2つ目の要素はピボットに使われる行を示すベクトル（置換行列と等価な置換ベクトル），3つ目の要素は推定条件数である．

次の例では，LUDecompositionの計算の3つの結果を示す：

LU分解の特徴のひとつに，下・上三角行列が同じ行列に保管されているということが挙げられる．個々の，要素は次のようにして得られる．疎行列に要素を掛け合せることによって，どのように要素のベクトル化操作が行われるかに留意のこと．これにより，処理がより効率的になる．詳細は「プログラミング効率」で述べる．

行列を生成する：

もとの行列は非特異であるので，これは行列の分解である．そのため，

と

を掛けるともとの行列を行ピボットベクトルで置換したものになる：

次に，もとの行列を置換したものから，

行列と

行列の積を引く．差はゼロに極めて近い：

行列の対角要素はピボットである．LU分解の最中にゼロピボットが現れたら，行列が特異であるということである．このようなときは，LUDecompositionは警告メッセージを発する：

コレスキー分解

対称正定値行列のコレスキー分解は，以下を満たす一意の上三角行列への分解である．

この分解はさまざまに使える．そのひとつに，三角行列の分解であるため，対称正定値行列を含む方程式の系の解法に使えるということが挙げられる（三角行列の分解で行列方程式を解く方法については「LU分解」で述べた）．行列がこのような形であることが分かっているなら，コレスキー分解の方が計算が速いため，LU分解よりも適している．コレスキー分解を使って行列方程式を解く場合は，コレスキーメソッドを使ってLinearSolveで直接行える．これについては前セクションで述べた．

Wolfram言語ではコレスキー分解は関数CholeskyDecompositionを使って行う．

CholeskyDecomposition[m]

コレスキー分解

次の式で，もとの行列が得られる：

行列が正定値行列でない場合は，コレスキー分解は存在しない：

正定値行列については，数多くの等価な定義がある．そのひとつが，すべてが正の固有値ということである：

行列が正定値行列であるかどうかを確認する方法のひとつに，コレスキー分解が存在するかどうかを調べるというものがある．

複素行列については，分解は共役転置で定義されている．以下で複素行列のコレスキー分解を計算する：

分解が正しいことを確認する：

コレスキー分解とLU分解

コレスキー分解とLU分解には，以下のような関係がある．

ここではピボットの対角行列である．

これは，以下のように示すことができる：

行列を計算する：

ピボットの行列を計算する：

最後にを計算する．この転置はコレスキー分解に等しい．

直交化

直交化法を使うと，任意の基底から正規直交基底が得られる．正規直交基底とは，以下を満たす基底である．

Wolfram言語では，関数Orthogonalizeを使ってベクトル一式を直交化することができる．

Orthogonalize[{v₁,v₂,…}]

定の実ベクトルリストから正規直交一式を生成する

の基底を形成する3つのベクトルを作成する：

ベクトルをプロットして可視化する．ベクトルはすべて同じ向きである：

正規直交基底を計算する：

明らかに正規直交ベクトルはより広がっている：

ベクトルv1，v2，v3は正規直交なので，各ベクトルのそれ自身との内積は1となる：

また，他のベクトルとの内積は0である：

Outerを使ってベクトルを他のすべてのベクトルと比べる：

デフォルトでグラム・シュミット(Gram–Schmidt)の直交化が計算されるが，他の直交化も多数計算することができる．

GramSchmidt
ModifiedGramSchmidt
Reorthogonalization
Householder

直交化のメソッド

以下ではHouseholderメソッドが使われている：

QR分解

列線形独立な長方行列をQR分解すると，以下を満たす行列，の計算が必要になる．

ここでの列はの列の直行基底を形成し，は上三角行列である，これはWolfram言語では関数QRDecompositionを使って計算できる．

QRDecomposition[m]

行列のQR分解

例題行列のQR分解を計算する．結果として2つの行列のリストが得られる：

返される引数の1つめは正規直交列のリストである．

行列を生成するには，転置を計算する必要がある：

行列の分解．

は

に等しい：

また，

の列は正規直交である．QRDecompositionの結果は列のリストを返すので，1つの部分指標で取り出せる．以下に列の正規直交特性を示す2つの例を挙げる：

QR分解は長方行列についても定義されている．次の例の場合，

である：

である入力行列について，QRDecompositionは結果として2つの行列を返す．1つは

行列

，もう1つは

行列

である．行列が方程式の過剰決定系を表している，つまり

であるなら，QRDecompositionは

行列

と

行列

を返す（行列

の生成には，QRDecompositionの結果を転置する必要がある）．以下にこれを例示する：

これはよくthin QR分解と呼ばれる．これについての例はGolub，van Loanの文献を参照のこと．完全なQR分解が必要なら，

をゼロ行で，

をゼロ列で充填することが可能である．これは次のような関数で行える：

この関数で計算した

と

は，それぞれ

，

である：

方程式系の解法

非特異の正方行列のQR分解は，LU分解と同様に，行列方程式を解くのに使用できる．しかし，長方行列の場合でも，QR分解は行列方程式を解くのに有用である．

QR分解の典型的な応用法のひとつに，過剰決定系の最小二乗解を求めるというものがある．これは以下の正規方程式系を解いて行う．

であるので，上式は以下のように簡約できる．

したがって，正規方程式は

のように簡約できる．は非特異であるため，さらに以下のようになる．

は三角行列なので，この系は簡単に解ける．この方法を実装するコードの例は「例題：最小二乗QR」を参照のこと．

特異値分解

長方行列の特異値分解では，以下を満たす直交行列，と対角行列の計算が行われる．

行列の対角成分は，の特異値と呼ばれる．Wolfram言語では，特異値は関数SingularValueList，完全な特異値分解は関数SingularValueDecompositionを使って計算する．

SingularValueList[m]	m の非零の特異値のリスト
SingularValueDecomposition[m]	m の特異値分解

次の計算は行列の分解なので，もとの行列に戻る：

行列

，

は直交しているので，もとの行列を直交変換して，特異値を対角成分に持つ対角行列を生成するのに使用できる：

行列が特異である場合は，特異値のいくつかはゼロとなる：

SingularValueListは非零の特異値のみを返す：

複素行列については，特異値分解の定義は共役転置を用いる．

特異値分解はさまざまな分野に応用できる．行列の特異値からは，で表される線形変換の情報が分かる．例えば，単位球にを作用させると，特異値を半軸とする楕円体となる．特異値は行列の階数の計算に使用できる．この場合，非零の特異値の数が階数である．特異値は2-ノルムの行列の計算にも使える．ゼロ特異値に対応する行列の列は，行列のゼロ空間である．

特異値の応用分野によっては，すべての特異値を必要としないこともある．Wolfram言語には特異値の一部のみを計算するメカニズムもある．

SingularValueList[m,k]	m の特異値の大きい方からk 個
SingularValueDecomposition[m,k]	m の対応する特異値分解
SingularValueList[m,-k]	m の特異値の小さい方からk 個
SingularValueDecomposition[m,-k]	m の対応する特異値分解

次の式は行列の最小の特異値を返す．最小の特異値はゼロなので，行列が最大階数でないことがわかる：

一般化特異値

× の行列および × の行列について，一般化された特異値は以下の分解の対で与えられる．

ここでは ×，は ×，は × であり，とは正規直交，は可逆である．

SingularValueList[{a,b}]	a と b の一般化された特異値
SingularValueDecomposition[{a,b}]	a と b の一般化された特異値分解

行列の例：

次の式は行列matA，matBの一般化された特異値を返す：

次は行列matA，matBの完全一般化特異値分解を計算する：

matAに対する同一性を示す：

matBに対する同一性を示す：

最後に，対応する対角要素の除算により特異値を求める：

オプション

関数SingularValueListとSingularValueDecompositionにはToleranceオプションが適用できる．

オプション名	デフォルト値
Tolerance	Automatic	小さな特異値をゼロとして扱うための許容範囲

このオプションは，特異値がゼロであるように扱われる大きさを指定するものである．デフォルトでは，最大の特異値の tol 分の1小さいものは削除される．ここで tol は機械数行列に対して100×$MachineEpsilonである．任意精度の行列については，tol はである．は行列の精度を示す．

この行列の最小の特異値は許容値のデフォルト設定よりわずかに大きい．これはゼロ特異値としては扱われない：

許容値の設定を大きくすると，小さな特異値がゼロとして扱われるようになる：

シューア(Schur)分解

正方行列の行列のシューア分解は，ユニタリ行列 U を求めることで行う．このユニタリ行列は，を相似変換して対角に1×1，2×2ブロックを持つブロック上三角行列を求めるのに使用できる（2×2ブロックは実行列の固有値の複素共役対に対応する）．このような形のブロック上三角行列は準上三角行列と呼ばれる．

シューア分解は必ず存在するため，の上三角行列への相似変換も必ず存在する．これは，行列の対角化で使用した固有空間の相似変換とは相反する．固有空間の相似変換は常に存在するわけではない．

SchurDecomposition[m]

行列のシューア分解

次の例では，行列をシューア分解する．結果は2つの行列のリストとなる：

行列

は行列を相似変換して上三角行列

を得るのに使用できる：

次の行列に関しては，行列の対角化が可能なので，より簡単な形を生成する相似変換が見つかる：

次の行列は，固有ベクトルの行列が特異なので，対角化できない：

しかし，シューア分解は可能である．行列は上三角行列に変換される：

次の例では，行列は複素固有値を持つ：

結果の行列

は対角に2×2のブロックを持つ：

行列

は，行列を相似変換して準上三角行列を得るのに使用できる．結果の上三角行列（対角に1×1ブロックを持つ）は複素数を含んでいることがあるが，オプションRealBlockFormを使って得られる．結果が上三角である（つまり，対角に1×1ブロックを持つ）場合，行列の固有値は常に対角上にある：

複素行列の場合は，シューア分解の定義において共役転置が使われ，結果として上三角行列が返される．次の複素行列を使ってこれを例示する：

次は結果がシューア分解の定義を満足することを示す：

の対角要素は

の固有値を含んでいる：

一般化されたシューア分解

× の行列，について，一般化されたシューア分解は以下のように定義されている．

ここで，とはユニタリ行列，は上三角行列，は準上三角行列である．

SchurDecomposition[{a,b}]

a と b の一般化されたシューア分解

いくつかの行列の例を使う：

次の式の結果は一般化されたシューア分解となる：

結果が分解の定義により構成されていることを示す：

実数を入力したとき，オプションRealBlockFormを使うと，複素数を含む結果と，上三角行列が得られる．

オプション

SchurDecompositionには以下の2つのオプションが使用できる．

オプション名	デフォルト値
Pivoting	False	ピボットとスケールの実行するかどうかの指定
RealBlockForm	True	複素固有値について2×2実数ブロックを返すかどうかの指定

SchurDecompositionのオプション

Pivotingは，結果の質を高めるためにピボットとスケールが使えるようにするオプションである．Trueと設定されているときは，ピボットとスケールが使え，への変更を表す行列が返される．この新しく得られた行列を使ってシューア分解の定義を表すと，以下のようになる．

以下の例では行列にピボットとスケールを使用する．PivotingがTrueのとき，必要に応じてピボットとスケールが使用され，追加の行列（ここではスケールのみを表す）が返される：

上三角行列に変換する：

の対角要素は

の固有値である：

ピボットとスケールを用いないでシューア分解を計算すると，

の対角要素は

の固有値に近くはならない．以下でPivotingオプションの有用性を示す：

オプションRealBlockFormは準上三角行列を結果として生成することを制御するものである．これがTrueである場合は，対角上に2×2のブロックを持つ結果が生成されることがある．Falseの場合は，結果は対角に1×1のブロックを持つ上三角行列（複素数を含むこともある）となる．これを以下の実行列で例示する．この行列は複素数の固有値を持ち，シューア分解は対角上に2×2のブロックを持つ：

RealBlockFormをFalseに設定すると，上三角行列