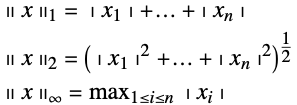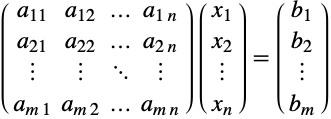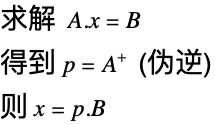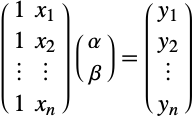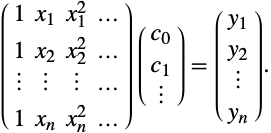在 Wolfram 语言的后续版本中引入了与本教程内容相关的附加功能. 最新信息请见矩阵和线性代数.

矩阵计算

基本运算	特征系统的计算
求解线性方程组	矩阵分解
最小二乘解	矩阵函数

本节教程将对所提供的用于进行矩阵计算的函数进行评述. 关于这些函数的更多信息可以在 Golub 和 van Loan 或 Meyer 等作者撰写的标准数学教科书中找到. 本节教程所介绍的运算，除了范数的计算也可扩展至标量和向量外，其它的计算都是矩阵所特有的.

基本运算

本节回顾了一些基本概念和运算，它们将贯穿整节教程，用于讨论矩阵运算.

范数

一个数学对象的范数是关于该对象的长度、尺寸或程度的度量. 在 Mathematica 中，范数存在于标量、向量和矩阵中.

Norm[num]	一个数的范数
Norm[vec]	向量的2范数
Norm[vec,p]	向量的 p 范数
Norm[mat]	矩阵的2范数
Norm[mat,p]	矩阵的 p 范数
Norm[mat,"Frobenius"]	矩阵的 Frobenius 范数

Mathematica 中范数的计算.

一个数的范数是其绝对值：

向量范数

在向量空间上，范数允许度量距离. 这使得对诸如邻域、近似接近度以及拟合优度等常见概念的定义成为可能. 向量范数是一个满足下述关系的函数 .

通常该函数用符号表示. 下标用于区分不同的范数，其中 p 范数尤其重要. 对于，p 范数的定义如下.

一些常见的 p 范数为1范数、2范数和范数.

在 Mathematica 中，向量 p 范数可以通过函数 Norm 计算. 下面的例子中得到了1范数、2范数和

范数：

2范数尤其有用，这是其默认值：

向量的范数用精确的数值输入表示：

向量的范数也可以用符号输入表示：

另外，如果使用的是符号 p，则结果也用该符号表示：

矩阵范数

矩阵范数用于给出矩阵空间上距离的度量. 如果要对矩阵之间的距离进行量化，例如一个矩阵接近于降秩矩阵，矩阵范数的存在是很有必要的.

矩阵范数也采用向量范数的双竖线表示符号. 最常见的矩阵范数之一是 Frobenius 范数（也称作 Euclidean 范数）.

另一个常见范数是 p 范数. 它们以向量 p 范数的形式进行定义如下.

因此，矩阵 p 范数表示矩阵可以应用于任何向量的最大扩展.

Mathematica 中 Frobenius 范数的计算可以按照下面所示进行：

矩阵2范数的计算如下所示：

也可以给定一个参数来指定1、2或

矩阵 p 范数：

这里计算由输入矩阵得到的不同向量的集合的扩展. 可以看到最大值仍小于2范数：

所有 p 范数均支持精确数值矩阵：

然而，对于符号表示的矩阵，只有1 和

矩阵 p 范数被支持：

零空间

与每个矩阵相关的基本子空间之一是零空间. 在一个矩阵的零空间的向量通过矩阵映射到零.

NullSpace[m]

一列基本向量，其线性组合满足

对于某些矩阵（例如，非降秩方阵），零空间为空：

该矩阵的零空间含有一个向量：

该矩阵的零空间有两个基本向量：

矩阵的秩

矩阵的秩对应于矩阵中线性无关的行或列的个数.

MatrixRank[mat]

给出矩阵 mat 的秩

如果一个 m×n 矩阵的各行不具有线性相关性，则它的秩等于

，这种情况被称作满秩：

如果一个矩阵的行之间存在任何相关性，它的秩必定小于

. 这种情况时，该矩阵被称为秩亏矩阵：

注意一个矩阵的秩等于其转置矩阵的秩. 这意味着线性无关的行数等于线性无关的列数：

对于一个 m×n 矩阵 A，下述关系成立：Length[NullSpace[A]]+ MatrixRank[A]n，且Length[NullSpace[A^T]]+ MatrixRank[A^T]m. 由此得到，当且仅当矩阵的秩等于 n 时零空间为空，并且当且仅当A 的秩等于 m 时 A 的转置矩阵的零空间为空.

如果秩与列数相等，则被称为满列秩；如果秩与行数相等，则被称为满行秩. 列梯形形式可以帮助理解矩阵的秩的概念.

简化行阶梯形式

将一个矩阵化简成行阶梯形式可以通过一组行变换实现，从左上角的元素所在的首元位置开始，将首元所在行以下的各行减去首元行的倍数，使得同一列中首元下方的所有元素为零. 然后选取位于下一行和下一列的元素作为下一个首元. 如果这一首元为零，并且其下方同一列中有非零元素，则进行行交换，并重复上面的步骤，直到进行到最后一行或最后一列为止.

如果对于一个矩阵的任意零行（行的各元素全部为零），其后的各行都是零行；并且如果行的第一个非零元素位于列，则第1至列位于下方的元素都为零，则该矩阵为行阶梯形式. 阶梯形矩阵并不唯一，但它的形式是唯一的，即各个首元的位置相同. 这也提供了一种用非零行个数确定矩阵的秩的方法.

如果一个行阶梯形矩阵，每个首元是1，并且每个首元所在的列的其它元素都为零，则称该矩阵是简化阶梯形矩阵.得到这种形式的步骤与得到行阶梯形矩阵的步骤类似，同样经过几步使首元简化成1（通过除法），将与首元所在列中首元上方的元素化简为零（通过减去当前首元行的倍数）. 矩阵的简化阶梯形式是唯一的.

简化行阶梯形式以及行阶梯形式提供了一种用非零行个数确定矩阵的秩的方法. 在 Mathematica 中，矩阵的简化行阶梯形式可以通过函数 RowReduce 计算得到.

RowReduce[mat]

给出矩阵 mat 的简化行阶梯形式

这个矩阵的简化行阶梯形式只有一个非零行，这说明矩阵的秩为1：

这是一个各列线性无关的3×2随机矩阵：

简化行阶梯形式有两个非零行；因此它的秩应该是2：

MatrixRank 计算得到的秩也是2：

转置矩阵的简化行阶梯形式也有两个非零行. 这与矩阵的秩与其转置矩阵的秩相等这一事实是一致的，即使矩阵是长方形也是如此：

矩阵的逆

方阵 A 的逆的定义如下：

其中为单位矩阵. 在 Mathematica 中，矩阵的逆可以通过函数 Inverse 得到.

Inverse[mat]

给出一个矩阵 mat 的逆

这是一个2×2样本矩阵：

这里表明矩阵符合定义：

不是所有矩阵都有逆；如果一个矩阵没有逆则被称作奇异矩阵. 如果矩阵是秩亏矩阵，则该矩阵是奇异的：

原则上矩阵的逆可用于求解矩阵方程

方法是在方程两边同乘以的逆.

然而，直接求解该矩阵方程往往更简单. 这些技巧将在"求解线性方程组"一节中讨论.

伪逆矩阵

对于奇异矩阵或非方阵矩阵，找到一个使最小化的近似逆仍然是可能的. 当使用2范数时，这将得到被称作伪逆矩阵的最小二乘解.

PseudoInverse[mat]

给出矩阵 mat 的伪逆矩阵

这将得到先前定义的奇异矩阵的伪逆矩阵：

结果不是单位矩阵，但接近于单位矩阵：

计算一个长方形矩阵的伪逆：

结果非常接近于单位矩阵：

通过伪逆得到的解是最小二乘解. 更多细节请见"最小二乘解"的讨论.

行列式

一个 n×n 矩阵的行列式定义如下.

它在 Mathematica 中可以通过函数 Det 计算得到.

Det[mat]	矩阵 mat 的行列式
Minors[mat]	矩阵 mat 的子式
Minors[mat,k]	mat 的 k 阶子式

这里是一个2×2样本矩阵：

行列式的一个非常有用的性质是：当且仅当

为奇异矩阵时，

：

正如已经指出的那样，如果矩阵是奇异的，则没有满秩：

子式

矩阵的子式是任意 k×k 子矩阵的行列式. 这个例子使用函数 Minors 来计算全部2×2子式：

子矩阵的大小可以通过一个第二选项控制. 这里计算得到了1×1子式，它们就是矩阵的各个项：

注意 Minors[m] 等价于 Minors[m,n-1]. 一般地，Minors[m,k] 计算矩阵 m 所有可能 k×k 子矩阵的行列式（这通过选取不同的 k 行和 k 列完成）. 对于一个 4×4 矩阵的 2×2 子式，将得到一个 6×6 矩阵，原因是从四行中选取2行或2列只有6种不同的方式：

矩阵的秩的一个性质是它等于最大非奇异子矩阵的大小. 这一点可以通过 Minors 进行示范. 在这个例子中，下述矩阵的秩为2：

矩阵的行列式为零：

当2×2子式计算得到后，可以看到不是所有子式都为零，这进一步证实矩阵的秩为2：

求解线性方程组

矩阵的重要用途之一是表示和求解线性方程组. 这一节讨论如何在 Mathematica 中求解线性方程组. 它充分利用为实现这一目的所提供的主要函数——LinearSolve.

求解一个线性方程组涉及到求解一个矩阵方程 . 由于是一个 × 矩阵，它代表的是含有个未知数的个线性方程的集合.

当时，方程组被称为正定. 意味着方程数大于未知数的个数，这时的方程组为超定方程组. 如果，则表示方程数小于未知数的个数，这时的方程组为欠定方程组.

square	m=n；解可以存在或不存在
overdetermined	m>n；解可以存在或不存在
underdetermined	m<n；无解或有无穷解
nonsingular	独立方程的个数等于变量的个数且行列式非零；存在唯一解
consistent	至少存在一个解
inconsistent	无解

由长方形矩阵所表示的线性方程组的类别.

需要注意的是，即使能够通过计算逆矩阵继而求解矩阵方程，这种方法并不值得推荐. 用户应该使用一种专门设计的函数来直接求解线性方程组，在 Mathematica 中，这由 LinearSolve 所提供.

LinearSolve[m,b]	求解矩阵方程 m.x==b 得到的向量 x
LinearSolve[m]	可重复应用在不同 b 的一个函数

通过 LinearSolve 求解线性方程组.

这里使用 LinearSolve 来求解一个矩阵方程：

该解可以进行测试，以证明它解决了问题：

您可以随时从输入矩阵中生成线性方程组：

然后应用 Solve 找到解：

LinearSolve 对于矩阵方程右首也是一个矩阵方程的情形同样有效：

对于超定系统，如果有解存在的话，LinearSolve 将得到一个解：

如果找不到解，则方程组不一致. 这时，找到最适合的解仍可能是有用的. 这通常用最小二乘技术完成，这将在"最小二乘解" 中探讨.

如果方程组欠定，则可能无解或者有无穷多的解，这时 LinearSolve 将返回一个：

当且仅当矩阵

与其增广矩阵（即在矩阵

的右边添上一列

所构成的矩阵）的秩相等时，该方程组是相容的. 下面的例子证明了先前的方程组是相容的：

LinearSolve 可用于 Mathematica 所支持的各种不同类型的矩阵，包括符号式、精确数值式、机器数值以及任意精度数所组成的各种矩阵. 它也可应用于密集与稀疏矩阵. 当稀疏矩阵用于LinearSolve 时，将采用适用于稀疏矩阵的专用技术，并且结果是解集向量：

选项名称	默认值
Method	Automatic	求解所用的方法
Modulus	0	取方程作为模 n
ZeroTest	(#0&)	用于零值测试符号法的函数

LinearSolve 的选项.

LinearSolve 有三种选项允许用户进行更多控制. 选项 Modulus 和 ZeroTest 用于符号技术，在"符号和精确矩阵"一节中讨论. 如果已知某些方法适用于某个具体问题，选项 Method 允许用户从这些方法中做出选择. 默认设置 Automatic 表示 LinearSolve 根据输入选择方法.

奇异矩阵

不存在逆矩阵的矩阵称为奇异矩阵. 测试奇异性的一种方式是计算行列式；如果是奇异矩阵，则行列式为零. 例如下面的矩阵是奇异的：

对于许多右端无解：

然而对于某些值解存在：

在第一个例子中，

的秩不等于增广矩阵的秩. 这进一步证实了方程组不相容，不能用LinearSolve 求解：

在第二个例子中，

的秩等于增广矩阵的秩. 这进一步证实了方程组相容，可以通过LinearSolve 求解：

对于无法找到解的情形，找到一个最适合的解仍是有可能的. 关于最适合的解的一种重要类别涉及到最小二乘解，这将在"最小二乘解"中讨论.

齐次方程

其次矩阵方程的右端是零.

如果矩阵是奇异的，这个方程有一个非零解. 可以通过计算行列式来测试一个矩阵是否奇异.

可以使用函数 NullSpace 得到齐次方程的解. 这将返回一个正交向量组，每个向量都是齐次方程的解. 在接下来的例子中，只有一个向量：

这里说明该解实际上解出了齐次方程：

函数 Chop 可用于替换接近0的近似数：

该齐次方程的解可以构成非齐次方程的无穷多个解. 这里解出了一个非齐次方程：

该解实际上就是方程的解：

如果在 sol 上增加一个任意因数与齐次方程的解的乘积，新的向量也是该矩阵方程的解：

准确性的估计和计算

对线性方程组解的准确性进行量化的一个重要途径是计算条件数 . 对于一个适当的范数选取，它的定义如下.

对于矩阵方程，可以证明的相对误差是乘以和的相对误差. 因此，条件数使解的准确性得到量化. 如果一个矩阵的条件数很大，该矩阵被称作“病态的”. 从病态矩阵中是不能期望得到一个好的解的. 对于某些过于病态的方程组，得到任何解都是不可能的.

在 Mathematica 中，条件数的近似值可以通过函数 LinearAlgebra`MatrixConditionNumber 计算得到.

LinearAlgebra`MatrixConditionNumber[mat]
	近似数值矩阵的无穷范数近似条件数
LinearAlgebra`MatrixConditionNumber[mat,Norm->p]
	一个矩阵的 p‐范数近似条件数，其中 p 的值可以为 1、2 或

这里计算得到一个矩阵的条件数：

该矩阵是奇异的，其条件数为

：

这个矩阵的条件数很大，被称为“病态的”：

如果一个矩阵与自身相乘，条件数增加：

如果求解的矩阵方程涉及到一个病态矩阵，结果可能不准确：

对于矩阵 mat2，这个解的准确性较低：

对付这类问题的方法是避免构建可能病态的矩阵，例如避免将矩阵与其自身相乘. 求解这类问题的另外一种方法是使用 Mathematica 中的任意精度计算；这将在"任意精度矩阵"中讨论：

符号和精确矩阵

LinearSolve 适用于可在 Mathematica 中表示的各种不同类型的矩阵. 有关于此的更多细节将在"矩阵类型"中介绍.

这里是一个关于纯符号矩阵的例子：

初始矩阵可以与解相乘：

相乘的结果需要通过 Simplify 进行某些后处理以达到期望值. 这表明了在线性代数符号计算中进行中间处理的需要. 如果不加考虑，这些中间结果可以变得非常大，使计算运行缓慢：

为了简化中间表达式，ZeroTest 选项可能派上用场.

LinearSolve 也可用于求解精确问题：

有许多专用于符号和精确计算的方法：CofactorExpansion，DivisionFreeRowReduction 以及 OneStepRowReduction. 这些将在"符号方法"一节中讨论.

行变换

行变换涉及到将多个行相加尽可能得到0元素. 最终得到的矩阵将是前面所介绍的简化行阶梯矩阵. 如果输入矩阵是非奇异方阵，结果将是一个单位矩阵：

这可以作为求解方程组的一种方法：

它可以与使用 LinearSolve 得到的结果进行比较：

因式分解的保存

线性方程组的许多应用涉及到同一矩阵

、但不同的方程右端

，因此常常要将因式分解保存以用于解决重复性问题. 在 Mathematica 中，这通过使用 LinearSolve 的单参数形式实现；这将返回一个泛函，用户可以将其应用到不同的向量得到相应的解：

当用户能够应用 LinearSolveFunction 到一个特定的右端时，即得到了解：

这里解出了矩阵方程：

不同的右端产生不同的解：

新的解解出了矩阵方程：

LinearSolve 的单参数形式与双参数形式的运行方式完全等价. 例如，它应用于输入矩阵的同一范围，返回符号式、精确或稀疏矩阵输入的预期结果. 它所接受的选项也相同.

单参数形式的一个问题是，对于一定的输入矩阵，其因式分解无法保存. 例如，对于超定方程组，精确解并不一定存在. 这种情况下，将生成一个警告信息，提示用户因式分解将在泛函每次应用于一个特定的右端时进行重复：

对于这个右端存在解，其返回如下：

然而，对于这个右端不存在解，将出现一个错误信息：

方法

LinearSolve 提供了不同的技术来求解针对与具体问题的矩阵方程. 用户可以使用选项 Method 对这些技术做出选择. 在这种方式下，提供了一个统一的接口，通向 Mathematica 所提供的用于求解矩阵方程的全部功能.

选项 Method 的默认设置是 Automatic，这表示该方程组将对所用的方法进行自动选择. 对于 LinearSolve，如果输入矩阵是数值型稠密矩阵，则将采用一种使用 LAPACK 的方法的例行程序；如果输入矩阵是数值型稀疏矩阵，则采用直接多波前法求解程序. 如果矩阵是符号型的，则使用专门的符号例行程序.

现在将详细介绍各种不同方法.

LAPACK

LAPACK 是求解密集数值矩阵的默认方法. 当矩阵为方阵且非奇异时，对于实数矩阵，例行程序是 dgesv、dlange 以及 dgecon，对于复数矩阵，例行程序是 zgesv、zlange 以及 zgecon. 当矩阵非方阵或奇异时，对于实数矩阵将使用 dgelss，对于复数矩阵，将使用 zgelss. 关于 LAPACK 的更多信息请见参考文献.

如果输入矩阵使用的是任意精度数值，则将采纳扩展至任意精度计算的 LAPACK算法.

多波前法

当输入矩阵为稀疏矩阵时，多波前法是一种默认使用的直接求解程序；它的选定也可以通过指定一个方法选项来实现.

这里读入一个以 Matrix Market 形式存储的样本稀疏矩阵. 关于矩阵导入的更多信息请见"稀疏矩阵的导入和导出"一节：

这里使用样本矩阵解出了矩阵方程：

如果多波前法所涉及到的输入矩阵是稠密型的，它将被转化成稀疏矩阵.

多波前法的执行使用的是"UMFPACK"程序库.

Krylov

Krylov 法是一种迭代求解程序，适用于大型稀疏线性方程组，诸如出现在偏微分方程的数值求解的方程组等. Mathematica 执行两种 Krylov 方法：共轭梯度（适用于正定对称矩阵）和 BiCGSTAB（适用于非对称方程组）. 使用适当的子选项对所用的方法以及一些其它参数进行设定是可能的.

选项名称	默认值
MaxIterations	Automatic	迭代的最大数量
Method	BiCGSTAB	求解所用的方法
Preconditioner	None	预调节器
ResidualNormFunction	Automatic	要最小化的范数
Tolerance	Automatic	使迭代终止所用的公差（tolerance）

Krylov 法的子选项.

BiCGSTAB 作为 Krylov 的默认方法，代价较高但适用性广. 共轭梯度方法适用于正定对称矩阵，总是收敛到一个解（尽管收敛可能会很慢）. 如果矩阵不是对称矩阵正定，共轭梯度可能不能收敛到一个解.

在这个例子中，矩阵不是对称正定矩阵，共轭梯度法不能收敛到一个解：

默认方法 BiCGSTAB 收敛并返回解：

对刚才找到的解进行测试：

下面这个例子显示了 Krylov 方法的优越性和预调节器的使用. 首先，定义了一个函数用于构建一个结构化的带状稀疏矩阵：

这里展示了由这个函数生成的矩阵的结构：

这里通过一个 10000×10000 矩阵建立了一个更大的方程组：

这将使用默认的稀疏求解程序，一个多波前法直接求解程序：

Krylov 法速度较快：

ILU 预调节器的适用使速度更快. 目前，只有当矩阵有非零对角线元素时，预调节器才能发挥效用：

当前只内置了 ILU 预调节器. 但用户仍可以通过定义一个应用于输入矩阵的函数来自定义预调节器. 下面是一个关于求解对角矩阵的例子.

首先设定一个问题，并在不使用预调节器的情况下对该问题求解：

现在将使用一个预调节器函数 fun；计算速度得到了显著提高：

一般来说，一个问题不会如此构造，使之能够受益于这样一个简单的预调节器. 但是，这个例子的用意在于它显示了如何创建和使用自定义的预调节器.

如果 Krylov 方法的输入矩阵是密集的，仍能得到这个结果，原因在于该方法基于的是矩阵/向量乘法.

Krylov 方法可用于求解对于直接求解程序来说过大的方程组. 然而，这不是通用的一般求解程序，主要适合于求解有某种形式的对角优势的问题.

Cholesky

Cholesky 方法适用于求解对称正定方程组：

对于这个矩阵来说，Cholesky 方法较快：

同时，Cholesky 方法更稳定. 这可以通过下面的矩阵说明：

对于这个矩阵，默认的 LU 方法生成一个潜在错误的报告：

Cholesky 方法能够成功求解：

对于密集矩阵，Cholesky 方法使用的是 LAPACK 函数，具体来说，对于实数矩阵使用的是 dpotrf 和 dpotrs 等，对于复数矩阵使用的是 zpotrf 和 zpotrs. 对于稀疏矩阵，Cholesky 方法使用"TAUCS"程序库.

符号方法

有一些方法专用于符号计算和精确计算：CofactorExpansion，DivisionFreeRowReduction 和 OneStepRowReduction. 这些方法可以通过下面的符号矩阵进行说明：

使用这三种方法重复计算：

最小二乘解

这一节与上一节相承. 它关注的是寻求到矩阵方程

的解，其中

是一个

矩阵，且

（即方程个数大于未知数个数）. 在这种情况下，解可能根本不存在，这时 LinearSolve 将发出一条错误提示：

在这些情形下，找到一个使最小的最合适的解是可能的. p 的一个非常通常选择是2；这样生成的是一个最小二乘解. 这是常用的，原因在于函数关于可微，并且在正交变换下2范数得以保存.

如果的秩为（即具有满列秩），可以表明（Golub 和 van Loan）最小二乘问题有一个能够求解方程组的唯一解.

这些被称作正规方程. 尽管可以直接求解这些正规方程得到最小二乘解，这种做法并不推荐使用，因为如果矩阵是病态的，则乘积将更病态. 对于满秩矩阵，得到最小二乘解的方法将在"范例：满秩最小二乘解"中探索.

值得注意的是，使其它范数如1和等最小化的最适当解同样可能. 适合于特定类型矩阵或使其它范数最小化的超定方程组的求解有许多方式，它们将在"1和无穷范数的最小化"一节中给出.

找到超定方程组的最小二乘解的一般方式是使用奇异值分解来形成矩阵的伪逆矩阵. 在 Mathematica 中，这通过 PseudoInverse 计算得到. 该技术对于秩亏的输入矩阵同样有效. 下面是该技术的要点.

这是一个超定方程组；可以看到矩阵

为秩亏矩阵：

仍能使用 PseudoInverse 找到最小二乘解：

这里表明解实际上的近似程度：

数据拟和

科学测量常常导致有序数据对集合 . 为了预测那些未经测量的点所对应的值，拟和一条通过数据点的曲线是很常见的. 如果曲线是一条直线，则致力于找到未知的系数和，使得

对于所有的数据对成立. 这可以写成如下所示的矩阵形式，并能立刻被识别为等价于求解一个超定线性方程组.

对于一个更一般的曲线的拟和，例如

等价于矩阵方程

这种情况时，左端的矩阵是一个 Vandermonde 矩阵. 事实上，可以使用任何未知系数为线性的函数.

现在将给出一个如果找到最适合参数的例子. 这将开始于下面所示的测量：

这些可以绘制成图形：

可以尝试使用"伪逆矩阵"中所介绍的 PseudoInverse 技术来求解. 首先，在数据分成

和

两部分：

形成右端的矩阵：

最佳参数可以按如下方式找到：

Mathematica 提供了函数 FindFit 来找到数据的最佳解. 解与通过 PseudoInverse 所找到的解一致：

最后，一个图形被绘制，显示了数据点和拟和后的曲线：

函数 FindFit 非常通用，它也能非线性参数的数据进行函数拟和.

特征系统的计算

特征值问题的解是矩阵计算的主要领域之一. 它在物理学、化学和工程上有许多应用. 对于一个 × 矩阵，特征值是它的特征多项式的个根. 根的集合，被称作矩阵的谱. 对于每个特征值，满足

的向量被称作特征向量. 特征向量的矩阵，如果存在且非奇异，则可用作相似变换形成一个对角矩阵，其中特征值作为对角元素. 特征值的许多重要应用涉及到这种方式下矩阵的对角化.

Mathematica 有许多函数来计算特征值和特征向量.

Eigenvalues[m]	m 的一列特征值
Eigenvectors[m]	m 的一列特征向量
Eigensystem[m]	一个形如{特征值，特征向量}的列表
CharacteristicPolynomial[m,x]	m 的特征多项式

特征值和特征向量.

这是一个2×2样本矩阵：

这里计算特征值：

这里计算特征向量：

通过 Eigensystem 可以同时计算特征值和特征向量：

可以证实第一个特征值及其特征向量符合定义：

应该注意的是，Eigenvectors 和 Eigensystem 返回的是一个特征向量列表. 这意味着如果要得到一个以特征向量为列的矩阵，必须进行转置. 这里表明，特征值及其对应的特征向量符合特征向量的定义：

也可以获得测试矩阵的特征多项式：

这里得到特征多项式的根；可以看到它们与矩阵的特征值匹配：

特征值计算既适用于稀疏矩阵，也适用于密集矩阵. 在下面的例子中，一个特征值为零：

一个特征值为零意味着矩阵的零空间非空：

特征值的某些应用不要求计算所有的特征值. Mathematica 提供了一种仅获得一部分特征值的机制.

Eigenvalues[m,k]	m 的最大的 k 个特征值
Eigenvectors[m,k]	m 的对应的特征向量
Eigenvalues[m,-k]	m 的最小的 k 个特征值
Eigenvectors[m,-k]	m 的对应的特征向量

如果矩阵非常大，这样做尤其有利. 这是一个 10000×10000 稀疏矩阵：

这是最大的特征值：

选项名称	默认值
Cubics	False	是否返回 3×3 矩阵的根式
Method	Automatic	求解所用的方法
Quartics	False	是否返回 4×4 矩阵的根式
ZeroTest	(#0&)	用于零值测试符号法的函数

用于 Eigensystem 的选项.

Eigensystem 有四个允许用户获得更多控制的选项. 选项 Cubics, Quartics 和 ZeroTest 用于符号技术，在"符号和精确矩阵"一节中讨论. 选项 Method 允许知识丰富的用户来选择专门适合他们的问题的方法；Automatic 的默认设置意味着 Eigensystem 选出了一个普遍使用的方法.

特征系统的性质

这一节将介绍特征系统计算的一些性质. 应该记住，由于一个 × 矩阵的特征值可以与一个次多项式的根紧密相关，特征值总为个.

即使一个矩阵只含有实数，它的特征值也未必是实数：

一个矩阵的特征值可以重复；不重复的特征值称作简单特征值. 在这个例子中，重复的特征值所含特征向量的个数与它所重复的次数相同，这被称作半简单特征值：

重复的特征值所含特征向量的个数可能小于它所重复的次数. 这时的特征值是一个缺损特征值，该矩阵被称作缺损矩阵：

矩阵可能有一个零特征值，但仍含有一个完整的特征向量集合：

矩阵可能有一个零特征值，但不含有一个完整的特征向量集合：

对于实数对称矩阵，所有的特征值为实数，并有一个特征向量的正交基：

这些特征向量是一个正交基：

具有正数特征值的对称实矩阵被称为正定：

具有非零特征值的对称实矩阵被称为半正定：

对于复数 Hermitian 矩阵（即等于其共轭转置），所有的特征值是实数，并且有一个特征向量的正交基：

这些特征向量是一个正交基：

具有正数特征值的 Hermitian 矩阵被称为正定：

矩阵对角化

特征系统计算的用途之一是提供一个使矩阵对角化的相似变换：

相似变换保留了矩阵的一些有用性质，例如行列式、秩和迹.

如果特征向量矩阵是奇异的，则矩阵不能被对角化. 如果矩阵为缺损的（即存在一个特征值不含有完整的特征向量集合），会发生这种情况，正如下例所示：

列特征向量矩阵是奇异的，因此不存在使得初始矩阵对角化的相似变换：

符号和精确矩阵

正如在 Mathematica 中所贯有的，如果计算的是一个符号或精确矩阵， Mathematica 将利用符号计算代数技术并返回一个符号或精确结果.

这是一个示范的 3×3 整数矩阵：

计算特征值，结果使用 Root 对象：

结果的机器精度近似值可以通过 N 计算得到：

通过设置选项 Cubics 为 True，结果可以以根式的形式返回：

广义特征值

对于 × 矩阵，其广义特征值为特征多项式的个根. 对于每一个广义特征值，满足

的向量被称作广义特征向量.

Eigenvalues[{a,b}]	a 和 b 的广义特征值
Eigenvectors[{a,b}]	a 和 b 的广义特征向量
Eigensystem[{a,b}]	a 和 b 的的广义特征系统

广义特征值和特征向量.

这是两个 2×2 矩阵：

计算广义特征值：

如果这两个矩阵具有一个共同的非零零空间，则将存在一个不确定的特征值：

这两个矩阵具有一个共同的一维零空间：

其中一个广义特征值为 Indeterminate：

方法

根据具体问题的不同，特征值计算将使用各种不同的技术. 用户可用通过选项 Method 对这些技术作出选择. 有一个通向 Mathematica 所有功能的统一的接口.

选项 Method 的默认设置是 Automatic. 按照 Mathematica 的惯例，这表示系统将会对所用方法自动做出选择. 在计算特征值时，如果输入的是一个机器数值的 × 矩阵，并且所求特征值的个数小于的 20%，则使用一种 Arnoldi 方法. 否则，如果输入矩阵是数值型的，则使用一种使用 LAPACK 例行程序的方法. 如果矩阵为符号型，则使用专门的符号例行程序.

现在详细介绍各种不同方法.

LAPACK

LAPACK 是计算特征值和特征向量全体集合的默认方法. 对于非对称矩阵，dgeev 用于实数矩阵，zgeev 用于复数矩阵. 对于对称矩阵，dsyevr 用于实数矩阵，zheevr 用于复数矩阵. 对于广义特征值，例行程序 dggev 用于实数矩阵，zggev 用于复数矩阵. 关于 LAPACK 的更多信息请见参考文献部分.

应该注意的是，对称矩阵的特征值计算较快，因为 Mathematica 能够探测到这种情形，并切换到合适的方法：

如果输入矩阵使用的是任意精度数值，则选用扩展至任意精度计算的 LAPACK 算法.

Arnoldi

Arnoldi 方法是一种迭代法，用于计算有限个特征值. 执行 Arnoldi 方法使用的是 "ARPACK" 程序库. 能够通过这种技术来求解的最一般的问题是选择计算下式的几个特征值：

因为它是一种迭代技术，仅能得到几个特征值，它常用于稀疏矩阵. 该技术的功能之一是能够应用一个偏移，并对给定的特征向量和特征值（）求解.

这对于找到临近的特征值很有效.

可以给 Arnoldi 方法赋予下列子选项.

选项名称	默认值
BasisSize	Automatic	Arnoldi 基的大小
Criteria	Magnitude	求解所用的方法
MaxIterations	Automatic	迭代最大次数
Shift	None	一个 Arnoldi 偏移
StartingVector	Automatic	所用的初始向量
Tolerance	Automatic	使迭代终止所用的公差

Arnoldi 方法的子选项.

这是一个 3×3 稀疏矩阵：

这里计算最大的特征值，指定使用 Arnoldi 方法：

计算临近-1的特征值：

如果给定的一个偏移与特征值一致，则会导致一条错误信息：

这里试图找到一个1500×1500 三对角矩阵的特征值，其中 2 在对角线上，-1 不在对角线上. 该算法不收敛：

如果算法不收敛，它将返回一个结果，但可能不很准确. 加速收敛的一种途径是使用作为偏移生成的结果：

得到收敛的另一种途径是增加迭代次数：

另外，在增加迭代次数的同时增大 Arnoldi 基也可以达到收敛. 在这个例子中，基增大后使算法经过较少次数的迭代就达到了收敛. 尽管对于每次迭代都更加耗时，但提高了总体计算速度：

与密集特征值计算相比，基为30的 Arnoldi 算法仍然常常要快，并且消耗内存较少.（应该注意的是具体耗时多少可能根据机器不同而不同.）

对于许多出现在实际计算中的大型稀疏方程组，Arnoldi 算法能够很快地收敛.

符号方法

Symbolic 特征值的计算通过特征多项式的差值来进行.

矩阵分解

这一节将讨论用于矩阵的一些标准技术. 这些技术常用作求解矩阵问题的构件. 分解属于因式分解、正交变换和相似变换的范畴.

LU 分解

矩阵的 LU 分解在求解矩阵方程时常用作高斯消去过程的一部分. 在 Mathematica 中，没有必要使用 LU 分解来求解矩阵方程，原因在于，正如在"求解线性方程组"一节中所讨论的，函数 LinearSolve 可以为您完成这个任务. 注意的是，如果您想要保存矩阵的分解以便用于求解具有相同左端的问题，可以像"因式分解的保存"一节中所示范的那样，使用 LinearSolve 的单参数形式.

非奇异方阵的部分主元消元法中的 LU 分解要计算独特的矩阵、以及，使得

其中是对角线元素均为1的下三角形式，是上三角形式，是置换矩阵. 一旦得到，可以通过找到下述等价方程组的解将其用于求解矩阵方程.

这可通过首先解出下式中的来完成.

然后关于求解，得到所要的解.

由于和均为三角矩阵，求解这些方程组尤其简单.

尽管在 Mathematica 中求解矩阵方程不需要使用 LU 分解，Mathematica 还是提供了函数 LUDecomposition 来计算 LU 分解.

LUDecomposition[m]

部分主元消元的 LU 分解

LUDecomposition 返回一个三元素的列表. 第一个元素是上下三角矩阵的结合，第二个元素是一个向量，用于指定主元消元所用的行（一个等价于置换矩阵的置换向量），第三个元素是条件数的估计值.

在这个例子中显示了 LUDecomposition 计算的三个结果：

LU 分解的特征之一是下矩阵和上矩阵被存在同一个矩阵中. 单独的和因子可以通过如下方法获得. 注意观察它们如何使用一种向量化的运算来完成稀疏矩阵的逐个元素的相乘. 这是的该过程更加有效；这些技术在"编程的效率"一节中进一步讨论.

生成

矩阵：

生成

矩阵：

初始矩阵非奇异，因此这是一个因式分解. 于是，将

与

相乘重新创建了通过行主元向量置换的初始矩阵：

下面从置换的初始矩阵中减去

和

的乘积. 两者相差接近于0：

矩阵的对角元素被称作主元. 如果在 LU 分解的计算过程中出现了任何零主元，则说明矩阵是奇异的. 这时，LUDecomposition 将生成一条警告信息：

Cholesky 分解

对称正定矩阵的 Cholesky 分解是一种因式分解，将其分解成一个唯一的上三角矩阵，使得

这种分解有很多用途，其中之一是，由于这是一个三角分解，它可用于对称正定矩阵的方程组. （三角因式分解如何用于求解矩阵方程在"LU 分解"一节中有说明.）如果已知一个矩阵是这种形式， Cholesky 分解将优于 LU 分解，因为 Cholesky 因式分解的计算较快. 如果想要使用 Cholesky 分解求解矩阵方程，可以使用 Cholesky 方法直接从LinearSolve 中完成，这在前面一节中介绍过.

Cholesky 因式分解可以通过函数 CholeskyDecomposition 计算.

CholeskyDecomposition[m]

Cholesky 分解

重新构建初始矩阵：

如果矩阵非正定，则 Cholesky 分解不存在：

与正定等价的定义有很多，例如特征值全部为正：

测试一个矩阵是否是正定的方式之一是看 Cholesky 分解是否存在.

注意如果矩阵是复数的，因式分解通过共轭转置定义. 下面计算一个复数矩阵的 Cholesky 分解：

这里表明因式分解是正确的：

Cholesky 和 LU 因式分解

Cholesky 和 LU 因式分解有如下关系

其中是主元的对角矩阵.

这可以通过下面进行说明：

现在可以计算

矩阵：

这一步计算主元矩阵：

最后，计算；它的转置等于 Cholesky 分解.

正交化

正交化从一个任意基生成一个正交基. 正交基指的是一个基，满足

在 Mathematica 中，一个向量集合可以通过函数 Orthogonalize 正交化.

Orthogonalize[{v₁,v₂,…}]

由给定的一列实数向量生成一个正交集

这里构造了一个三向量的集合，形成

的一个基：

这个图形可以直观向量；它们都倾向于同一方向：

计算一个正交基：

正交向量明显分散开来：

向量 v1, v2 和 v3 是正交向量，即每个向量与自身的点积是1：

另外，一个向量与其它向量的点积为0：

这里使用 Outer 来将所有向量与其它向量进行比较：

默认时计算的是 Gram–Schmidt 正交化，但也能计算许多其它的正交化.

GramSchmidt
ModifiedGramSchmidt
Reorthogonalization
Householder

正交化方法.

这里使用 Householder 方法：

QR 分解

一个矩形矩阵线性无关列的 QR 分解要计算矩阵和，使得

其中中各列形成中各列的一个正交基，是一个上三角矩阵. 它可以通过函数 QRDecomposition 计算.

QRDecomposition[m]

一个矩阵的 QR 分解

计算一个示范矩阵的 QR 分解. 结果是一个由两个矩阵组成的列表：

事实上，返回的第一个参数是一个正交列的列表. 要生成矩阵

，有必要计算转置：

这是一个矩阵因式分解，因此

等于

：

另外，

的各列是正交的. 由于 QRDecomposition 的结果返回的是列列表，它们可以用一部分指标提取. 下面两个例子都说明了列的正交特性：

QR 分解也为矩形矩阵定义. 这时，

：

对于一个

的输入矩阵，QRDecomposition 的结果是两个矩阵：一个

矩阵

和一个

矩阵

. 当矩阵表示的是一个超定方程组（即

）时，QRDecomposition 返回一个

矩阵

和一个

矩阵

. （注意要生成矩阵

，有必要将 QRDecomposition 得到的结果进行转置.) 这通过下面的例子进行说明：

这通常被称为单薄 QR 分解；见 Golub 和 van Loan 中的例子. 如果想要计算完全 QR 分解，用多余的零行和带有多余正交列的

对

进行填充，是可能做到的. 这可以通过下述函数完成：

通过这个函数计算得到的

和

分别是

与

：

求解方程组

对于非奇异方阵，QR 分解可用于求解矩阵方程，这一点与 LU 分解的情形相同. 然而，如果矩阵是矩形的， QR 分解同样可用于求解矩阵方程.

QR 分解的一个特别应用是通过求解下述正规方程组，找寻超定方程组的最小二乘解

由于，这可以简化为

因此正规方程组简化为

，由于非奇异，该式简化为

由于为三角矩阵，这个方程组的求解非常简单；在 "范例：最小二乘 QR"中给出了执行这个操作所用的简单程序代码.

奇异值分解

矩形矩阵的奇异值分解涉及到正交矩阵和与一个对角矩阵的计算，使得下式成立

矩阵的对角元素被称作的奇异值. 在 Mathematica 中，函数 SingularValueList 计算奇异值，函数 SingularValueDecomposition 计算完全奇异值分解.

SingularValueList[m]	m 的非零奇异值的一个列表
SingularValueDecomposition[m]	m 的奇异值分解

这个因式分解使得，使初始矩阵得以恢复：

由于

和

是正交矩阵，它们可用于初始矩阵的正交变换，从而得到奇异值在对角线上的对角矩阵：

如果该矩阵是奇异的，则一部分奇异值将为零：

SingularValueList 仅返回非零的奇异值：

注意的是，对于复数矩阵，奇异值分解的定义使用共轭转置.

奇异值分解有许多应用. 矩阵的奇异值提供所表示的线性变换的信息. 例如，在一个单位球面上的行为生成一个椭圆体，其半轴由奇异值给定. 非零奇异值的个数等于矩阵的秩，因此奇异值可用于计算矩阵的秩. 奇异值可用于计算矩阵的2范数，与零奇异值对应的矩阵的各列是矩阵的零空间.

奇异值的一些应用不要求计算所有的奇异值. Mathematica 提供了一种机制来获得部分奇异值.

SingularValueList[m,k]	m 的最大的 k 个奇异值
SingularValueDecomposition[m,k]	m 对应的奇异值分解
SingularValueList[m,-k]	m 的最小的 k 个奇异值
SingularValueDecomposition[m,-k]	m 对应的奇异值分解

返回输入矩阵的最小的奇异值；由于该值为零，这说明输入矩阵不是满秩矩阵：

广义奇异值

对于一个 × 矩阵和一个 × 矩阵，广义奇异值由因式分解对

给出，其中为 ×，为 ×，为 ×；和是正交矩阵，是可逆矩阵.

SingularValueList[{a,b}]	a 和 b 的广义奇异值
SingularValueDecomposition[{a,b}]	a 和 b 的广义奇异值分解

这是两个示范矩阵：

这里返回矩阵 matA 和 matB 的广义奇异值：

计算矩阵 matA 和 matB 的完全广义奇异值分解：

这里显示的是 matA 的单位矩阵：

这里显示的是 matB 的单位矩阵：

最后，奇异值通过与对应的对角元素相除得到：

选项

函数 SingularValueList 和 SingularValueDecomposition 都可以使用一个 Tolerance 选项.

选项名称	默认值
Tolerance	Automatic	当小奇异值视为零的公差

该选项控制的是将奇异值当作零处理的公差范围. 默认时，小于最大奇异值 tol 倍的值将被去除. 对于机器数值矩阵，tol 等于 100×$MachineEpsilon. 对于任意精度矩阵，它等于，其中是该矩阵的精确度.

这个矩阵的最小奇异值仅略大于公差的默认设置. 它将不被视作一个零奇异值：

增加公差的设置会导致将最小奇异值视作零：

Schur 分解

方阵的 Schur 分解涉及到找寻一个酉矩阵，使之用于的相似变换，从而形成一个上三角矩阵块，其中对角线上是1×1 和 2×2 矩阵块（该 2×2 矩阵块对应于实数矩阵的特征值的复数共轭对）. 这种形式的上三角矩阵块可以被称作上准三角.

Schur 分解始终存在，因此的相似变换也始终存在. 这一点与矩阵的对角化中所用的特征系统相似变换冲突，后者并不始终存在.

SchurDecomposition[m]

矩阵的 Schur 分解

计算一个示范矩阵的 Schur 分解. 结果是有两个矩阵组成的列表：

矩阵

可用于该矩阵的相似变换，来生成上三角

：

对于这个特殊矩阵，可以找到一个生成更简单形式的相似变换，因为矩阵可对角化：

这个矩阵不能对角化，原因是特征向量矩阵是奇异的：

然而可以进行 Schur 分解，并且该矩阵被变换成一个上三角形式：

在这个例子中，该矩阵存在复数特征值：

现在生成的矩阵

在对角线上有一个 2×2 矩阵块：

矩阵

可用于矩阵的相似变换，生成上准三角. 注意的是，可能涉及复数的上三角结果（对角线上是 1×1 矩阵块）可以通过使用选项 RealBlockForm 获得. 如果结果是上三角（即在对角线上有 1×1 矩阵块），矩阵的特征值总是在对角线上：

注意如果矩阵是复数的，Schur 分解按照定义使用共轭转置并返回一个上三角结果. 这将通过下面的复数矩阵说明：

这里说明该结果符合 Schur 分解的定义：

的对角线包含

的特征值：

广义 Schur 分解

对于 × 矩阵和，广义 Schur 分解定义为

其中和为酉矩阵，是上三角矩阵，是上准三角矩阵.

SchurDecomposition[{a,b}]

a 和 b 的广义 Schur 分解

这里是两个示范矩阵：

返回广义 Schur 分解：

这表明结果与分解的定义一致：

对于实数输入，通过选项 RealBlockForm 可以获得一个复数结果和一个上三角结果.

选项

SchurDecomposition 有两个选项可取.

选项名称	默认值
Pivoting	False	是否进行旋转和缩放
RealBlockForm	True	对于复数特征值是否返回 2×2 实数矩阵块

用于 SchurDecomposition 的选项.

选项 Pivoting 可允许旋转和缩放从而改善结果的质量. 如果设置是 True，即允许旋转和缩放，返回一个矩阵来代表对所作的改变. 对于这个新矩阵，Schur 分解的定义可以从下式看出.

现在在此说明旋转和缩放对于下述矩阵的用途. 当 Pivoting 设置为 True 时，旋转和缩放在必要时使用，并且返回一个仅表示缩放的附加矩阵：

这表示一个上三角形式的变换：

的对角元素是

的特征值：

如果 Schur 分解的计算不进行旋转和缩放，

的对角元素就比较远离

的特征值. 这说明了 Pivoting 选项的用途：

选项 RealBlockForm 控制上准三角结果的生成. 如果设置为 True，生成的结果可能在对角线上含有 2×2 矩阵块. 如果设置为 False，结果将是一个上三角，其对角线上是 1×1 矩阵（单可能涉及复数数值）. 这通过下面的实数矩阵说明，该矩阵有复数特征值，并有一个 Schur 分解，在对角线上有 2×2 矩阵块：

设置 RealBlockForm 为 False 生成一个上三角形式的矩阵