Strings and Characters
Strings and Characters
| Properties of Strings | Special Characters in Strings |
| Operations on Strings | Newlines and Tabs in Strings |
| Characters in Strings | Character Codes |
| String Patterns | Raw Character Encodings |
| Regular Expressions |
Much of what the Wolfram Language does revolves around manipulating structured expressions. But you can also use the Wolfram Language as a system for handling unstructured strings of text.
When you input a string of text to the Wolfram Language, you must always enclose it in quotes. However, when the Wolfram Language outputs the string, it usually does not explicitly show the quotes.
You can see the quotes by asking for the input form of the string. In addition, in a Wolfram System notebook, quotes will typically appear automatically as soon as you start to edit a string.
The fact that the Wolfram Language does not usually show explicit quotes around strings makes it possible for you to use strings to specify quite directly the textual output you want.
You should understand, however, that even though the string "x" often appears as x in output, it is still a quite different object from the symbol x.
You can test whether any particular expression is a string by looking at its head. The head of any string is always String.
All strings have head String:
You can use strings just like other expressions as elements of patterns and transformations. Note, however, that you cannot assign values directly to strings.
The Wolfram Language provides a variety of functions for manipulating strings. Most of these functions are based on viewing strings as a sequence of characters, and many of the functions are analogous to ones for manipulating lists.
| s1<>s2<>… or StringJoin[{s1,s2,…}] | join several strings together |
| StringLength[s] | give the number of characters in a string |
| StringReverse[s] | reverse the characters in a string |
StringLength gives the number of characters in a string:
StringReverse reverses the characters in a string:
| StringTake[s,n] | make a string by taking the first n characters from s |
| StringTake[s,{n}] | take the n th character from s |
| StringTake[s,{n1,n2}] | take characters n1 through n2 |
| StringDrop[s,n] | make a string by dropping the first n characters in s |
| StringDrop[s,{n1,n2}] | drop characters n1 through n2 |
StringTake and StringDrop are the analogs for strings of Take and Drop for lists. Like Take and Drop, they use standard Wolfram Language sequence specifications, so that, for example, negative numbers count character positions from the end of a string. Note that the first character of a string is taken to have position 1.
| StringInsert[s,snew,n] | insert the string snew at position n in s |
| StringInsert[s,snew,{n1,n2,…}] | insert several copies of snew into s |
StringInsert[s,snew,n] is set up to produce a string whose n th character is the first character of snew.
This uses Riffle to add a space between the words in a list:
| StringReplacePart[s,snew,{m,n}] | replace the characters at positions m through n in s by the string snew |
| StringReplacePart[s,snew,{{m1,n1},{m2,n2},…}] | replace several substrings in s by snew |
| StringReplacePart[s,{snew1,snew2,…},{{m1,n1},{m2,n2},…}] | replace substrings in s by the corresponding snewi |
| StringPosition[s,sub] | give a list of the starting and ending positions at which sub appears as a substring of s |
| StringPosition[s,sub,k] | include only the first k occurrences of sub in s |
| StringPosition[s,{sub1,sub2,…}] | include occurrences of any of the subi |
You can use StringPosition to find where a particular substring appears within a given string. StringPosition returns a list, each of whose elements corresponds to an occurrence of the substring. The elements consist of lists giving the starting and ending character positions for the substring. These lists are in the form used as sequence specifications in StringTake, StringDrop and StringReplacePart.
| StringCount[s,sub] | count the occurrences of sub in s |
| StringCount[s,{sub1,sub2,…}] | count occurrences of any of the subi |
| StringFreeQ[s,sub] | test whether s is free of sub |
| StringFreeQ[s,{sub1,sub2,…}] | test whether s is free of all the subi |
| StringContainsQ[s,sub] | test whether s contains sub |
| StringContainsQ[s,{sub1,sub2,…}] | test whether s contains any of the subi |
| StringStartsQ[s,sub] | test whether s starts with sub |
| StringStartsQ[s,{sub1,sub2,…}] | test whether s starts with any of the subi |
| StringEndsQ[s,sub] | test whether s ends with sub |
| StringEndsQ[s,{sub1,sub2,…}] | test whether s ends with any of the subi |
| StringReplace[s,sb->sbnew] | replace sb by sbnew wherever it appears in s |
| StringReplace[s,{sb1->sbnew1,sb2->sbnew2,…}] | replace sbi by the corresponding sbnewi |
| StringReplace[s,rules,n] | do at most n replacements |
| StringReplaceList[s,rules] | give a list of the strings obtained by making each possible single replacement |
| StringReplaceList[s,rules,n] | give at most n results |
StringReplace scans a string from left to right, doing all the replacements it can, and then returning the resulting string. Sometimes, however, it is useful to see what all possible single replacements would give. You can get a list of all these results using StringReplaceList.
| StringSplit[s] | split s into substrings delimited by whitespace |
| StringSplit[s,del] | split at delimiter del |
| StringSplit[s,{del1,del2,…}] | split at any of the deli |
| StringSplit[s,del,n] | split into at most n substrings |
| StringSplit[s,del->rhs] | insert rhs at the position of each delimiter |
| StringSplit[s,{del1->rhs1,del2->rhs2,…}] | insert rhsi at the position of the corresponding deli |
| Sort[{s1,s2,s3,…}] | sort a list of strings |
Sort sorts strings into standard dictionary order:
| StringTrim[s] | trim whitespace from the beginning and end of s |
| StringTrim[s,patt] | trim substrings matching patt from the beginning and end |
| SequenceAlignment[s1,s2] | find an optimal alignment of s1 and s2 |
| Characters["string"] | convert a string to a list of characters |
| StringJoin[{"c1","c2",…}] | convert a list of characters to a string |
StringJoin converts the list of characters back to a single string:
| DigitQ[string] | test whether all characters in a string are digits |
| LetterQ[string] | test whether all characters in a string are letters |
| UpperCaseQ[string] | test whether all characters in a string are uppercase letters |
| LowerCaseQ[string] | test whether all characters in a string are lowercase letters |
Not all the letters are uppercase, so the result is False:
| ToUpperCase[string] | generate a string in which all letters are uppercase |
| ToLowerCase[string] | generate a string in which all letters are lowercase |
| CharacterRange["c1","c2"] | generate a list of all characters from c1 and c2 |
CharacterRange will usually give meaningful results for any range of characters that have a natural ordering. The way CharacterRange works is by using the character codes that the Wolfram Language internally assigns to every character.
An important feature of string manipulation functions like StringReplace is that they handle not only literal strings but also patterns for collections of strings.
You can specify patterns for strings by using string expressions that contain ordinary strings mixed with Wolfram Language symbolic pattern objects.
| s1~~s2~~… or StringExpression[s1,s2,…] | |
a sequence of strings and pattern objects | |
| StringMatchQ["s",patt] | test whether "s" matches patt |
| StringFreeQ["s",patt] | test whether "s" is free of substrings matching patt |
| StringContainsQ["s",patt] | test whether "s" contains substrings matching patt |
| StringStartsQ["s",patt] | test whether "s" starts with a substring matching patt |
| StringEndsQ["s",patt] | test whether "s" ends with a substring matching patt |
| StringCases["s",patt] | give a list of the substrings of "s" that match patt |
| StringCases["s",lhs->rhs] | replace each case of lhs by rhs |
| StringPosition["s",patt] | give a list of the positions of substrings that match patt |
| StringCount["s",patt] | count how many substrings match patt |
| StringReplace["s",lhs->rhs] | replace every substring that matches lhs |
| StringReplaceList["s",lhs->rhs] | give a list of all ways of replacing lhs |
| StringSplit["s",patt] | split s at every substring that matches patt |
| StringSplit["s",lhs->rhs] | split at lhs, inserting rhs in its place |
You can use all the standard Wolfram Language pattern objects in string patterns. Single blanks (_) always stand for single characters. Double blanks (__) stand for sequences of one or more characters.
| "string" | a literal string of characters |
| _ | any single character |
| __ | any sequence of one or more characters |
| ___ | any sequence of zero or more characters |
| x_
,
x__
,
x___ | substrings given the name x |
| x:pattern | pattern given the name x |
| pattern.. | pattern repeated one or more times |
| pattern... | pattern repeated zero or more times |
| {patt1,patt2,…} or patt1|patt2|… | a pattern matching at least one of the patti |
| patt/;cond | a pattern for which cond evaluates to True |
| pattern?test | a pattern for which test yields True for each character |
| Whitespace | a sequence of whitespace characters |
| NumberString | the characters of a number |
| charobj |
an object representing a character class (see below)
|
| RegularExpression["regexp"] | substring matching a regular expression |
You can use standard Wolfram Language constructs such as Characters["c1c2…"] and CharacterRange["c1","c2"] to generate lists of alternative characters to use in string patterns.
In addition to allowing explicit lists of characters, the Wolfram Language provides symbolic specifications for several common classes of possible characters in string patterns.
| {"c1","c2",…} | any of the "ci" |
| Characters["c1c2…"] | any of the "ci" |
| CharacterRange["c1","c2"] | any character in the range "c1" to "c2" |
| DigitCharacter | digit 0–9 |
| LetterCharacter | letter |
| WhitespaceCharacter |
space, newline, tab or other whitespace character
|
| WordCharacter | letter or digit |
| Except[p] | any character except ones matching p |
String patterns are often used as a way to extract structure from strings of textual data. Typically this works by having different parts of a string pattern match substrings that correspond to different parts of the structure.
ToExpression converts them to ordinary symbols and numbers:
In many situations, textual data may contain sequences of spaces, newlines or tabs that should be considered "whitespace" and perhaps ignored. In the Wolfram Language, the symbol Whitespace stands for any such sequence.
String patterns normally apply to substrings that appear at any position in a given string. Sometimes, however, it is convenient to specify that patterns can apply only to substrings at particular positions. You can do this by including symbols such as StartOfString in your string patterns.
| StartOfString | start of the whole string |
| EndOfString | end of the whole string |
| StartOfLine | start of a line |
| EndOfLine | end of a line |
| WordBoundary | boundary between word characters and others |
| Except[StartOfString]
, etc.
| anywhere except at the particular positions StartOfString etc. |
String patterns allow the same kind of /; and other conditions as ordinary Wolfram Language patterns.
When you give an object such as x__ or e.. in a string pattern, the Wolfram Language normally assumes that you want this to match the longest possible sequence of characters. Sometimes, however, you may instead want to match the shortest possible sequence of characters. You can specify this using Shortest[p].
| Longest[p] | the longest consistent match for p (default) |
| Shortest[p] | the shortest consistent match for p |
Shortest specifies that instead the shortest possible match should be found:
The Wolfram Language by default treats characters such "X" and "x" as distinct. But by setting the option IgnoreCase->True in string manipulation operations, you can tell the Wolfram Language to treat all such uppercase and lowercase letters as equivalent.
| IgnoreCase->True | treat uppercase and lowercase letters as equivalent |
In some string operations, one may have to specify whether to include overlaps between substrings. By default, StringCases and StringCount do not include overlaps, but StringPosition does.
StringPosition includes overlaps by default:
| Overlaps->All | include all overlaps |
| Overlaps->True | include at most one overlap beginning at each position |
| Overlaps->False | exclude all overlaps |
General Wolfram Language patterns provide a powerful way to do string manipulation. But particularly if you are familiar with specialized string manipulation languages, you may sometimes find it convenient to specify string patterns using regular expression notation. You can do this in the Wolfram Language with RegularExpression objects.
| RegularExpression["regex"] | a regular expression specified by "regex" |
RegularExpression in the Wolfram Language supports all standard regular expression constructs.
| c | the literal character c |
| . | any character except newline |
| [c1c2…] | any of the characters ci |
| [c1-c2] | any character in the range c1–c2 |
| [^c1c2…] | any character except the ci |
| p* | p repeated zero or more times |
| p+ | p repeated one or more times |
| p? | zero or one occurrence of p |
| p{m,n} | p repeated between m and n times |
| p*?
,
p+?
,
p?? | the shortest consistent strings that match |
| (p1p2…) | strings matching the sequence p1p2… |
| p1|p2 | strings matching p1 or p2 |
There is a close correspondence between many regular expression constructs and basic general Wolfram Language string pattern constructs.
| . | _
(strictly
Except["∖n"]
)
|
| [c1c2…] | Characters["c1c2…"] |
| [c1-c2] | CharacterRange["c1","c2"] |
| [^c1c2…] | Except[Characters["c1c2…"]] |
| p* | p... |
| p+ | p.. |
| p? | p|"" |
| p*?
,
p+?
,
p?? | Shortest[p…],… |
| (p1p2…) | (p1~~p2~~…) |
| p1|p2 | p1|p2 |
Just as in general Wolfram Language string patterns, there are special notations in regular expressions for various common classes of characters. Note that you need to use double backslashes (∖∖) to enter most of these notations in Wolfram Language regular expression strings.
| \\d | |
| \\D | |
| \\s | |
| \\S | |
| \\w | |
| \\W | |
| [[:class:]] | characters in a named class |
| [^[:class:]] | characters not in a named class |
The Wolfram Language supports the standard POSIX character classes alnum, alpha, ascii, blank, cntrl, digit, graph, lower, print, punct, space, upper, word and xdigit.
In general Wolfram Language patterns, you can use constructs like x_ and x:patt to give arbitrary names to objects that are matched. In regular expressions, there is a way to do something somewhat like this using numbering: the n th parenthesized pattern object (p) in a regular expression can be referred to as \\n within the body of the pattern, and $n outside it.
In addition to the ordinary characters that appear on a standard keyboard, you can include in Wolfram Language strings any of the special characters that are supported by the Wolfram Language.
In a Wolfram System notebook, a special character such as 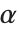 can always be displayed directly. But if you use a text‐based interface, then often the only characters that can readily be displayed are the ones that appear on your keyboard. Exactly which special characters can be displayed is inferred from the value of $CharacterEncoding.
can always be displayed directly. But if you use a text‐based interface, then often the only characters that can readily be displayed are the ones that appear on your keyboard. Exactly which special characters can be displayed is inferred from the value of $CharacterEncoding.
As a result, what the Wolfram System does in such situations is to try to approximate special characters by similar‐looking sequences of ordinary characters. And when this is not practical, the Wolfram System just gives the full name of the special character.
In a Wolfram System notebook using StandardForm, special characters can be displayed directly:
In OutputForm, however, special characters that cannot be displayed exactly are approximated when possible by sequences of ordinary ones:
When using InputForm or FullForm, special characters are not approximated. The Wolfram Language uses full names for non-representable special characters in InputForm, while FullForm always uses long names, even in the notebook interface.
In InputForm, all characters not part of the encoding—in this case the special characters other than é—are written using long names:
In FullForm, all special characters are written using long names:
By default, the Wolfram System uses the character encoding "PrintableASCII" when saving notebooks and packages. This means that when special characters are written out to files or external programs, they are represented purely as sequences of ordinary characters. This uniform representation is crucial in allowing special characters in the Wolfram Language to be used in a way that does not depend on the details of particular computer systems.
| a | a literal character |
\[Name]
| a character specified using its full name |
\"
| a " to be included in a string |
\\
| a \ to be included in a string |
You should realize that even though it is possible to achieve some formatting of Wolfram Language output by creating strings that contain raw tabs and newlines, this is rarely a good idea. Typically a much better approach is to use the higher-level Wolfram Language formatting primitives discussed in "String-Oriented Output Formats", "Output Formats for Numbers" and "Tables and Matrices". These primitives will always yield consistent output, independent of such issues as the positions of tab settings on a particular device.
The front end formatting construct Column gives more control. Here text is aligned on the right:
| ToCharacterCode["string"] | give a list of the character codes for the characters in a string |
| FromCharacterCode[n] | construct a character from its character code |
| FromCharacterCode[{n1,n2,…}] | construct a string of characters from a list of character codes |
The Wolfram Language assigns every character that can appear in a string a unique character code. This code is used internally as a way to represent the character.
FromCharacterCode reconstructs the original string:
| CharacterRange["c1","c2"] | generate a list of characters with successive character codes |
The Wolfram Language assigns names such as ∖[Alpha] to a large number of special characters. This means that you can always refer to such characters just by giving their names, without ever having to know their character codes.
The Wolfram Language has names for all the common characters that are used in mathematical notation and in standard European languages. But for languages such as Japanese, Chinese and Korean, there are thousands of additional characters, and the Wolfram Language does not assign an explicit name to each of them. Instead, it refers to such characters by standardized character codes.
In FullForm, these characters are referred to by standardized character codes. The character codes are given in hexadecimal:
The notebook front end for the Wolfram System is set up so that when you enter a character, the Wolfram System will automatically work out the character code for that character.
Sometimes, however, you may find it convenient to be able to enter characters directly using character codes.
| ∖.nn | a character with hexadecimal code nn |
| \:nnnn | a character with hexadecimal code nnnn |
| \|nnnnnn | a character with hexadecimal code nnnnnn |
For characters with character codes below 256, you can use \.nn. For characters with character codes above 256, you must use either \:nnnn or \|nnnnnn. Note that in all cases you must give a fixed number of hexadecimal digits, padding with leading 0s if necessary.
This enters the characters using their character codes. Note the leading 0 inserted in the character code for 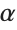 :
:
In assigning codes to characters, the Wolfram Language follows three compatible standards: ASCII, ISO Latin‐1 and Unicode. ASCII covers the characters on a normal American English keyboard. ISO Latin‐1 covers characters in many European languages. Unicode is a more general standard that defines character codes for several tens of thousands of characters used in languages and notations around the world.
0–127 (∖.00–∖.7f) | ASCII characters |
1–31 (∖.01–∖.1f) | ASCII control characters |
32–126 (∖.20–∖.7e) | printable ASCII characters |
97–122 (∖.61–∖.7a) | lowercase English letters |
129–255 (∖.81–∖.ff) | ISO Latin‐1 characters |
192–255 (∖.c0–∖.ff) | letters in European languages |
0–59391 (∖:0000–∖:e7ff) | Unicode standard public characters |
913–1009 (∖:0391–∖:03f1)
| Greek letters |
12288–35839 (∖:3000–∖:8bff)
|
Chinese, Japanese, and Korean characters
|
8450–8504 (∖:2102–∖:2138)
| modified letters used in mathematical notation |
8592–8677 (∖:2190–∖:21e5)
| arrows |
8704–8945 (∖:2200–∖:22f1)
| mathematical symbols and operators |
61440–63487 (∖:f000–∖:f7ff)
| Unicode private characters defined specially by the Wolfram Language |
Here are some special characters used in mathematical notation. The empty boxes correspond to characters not available in the current font:
The Wolfram Language always allows you to refer to special characters by using names such as ∖[Alpha] or explicit hexadecimal codes such as ∖:03b1. And when the Wolfram Language writes out files, it by default uses these names or hexadecimal codes.
But sometimes you may find it convenient to use raw encodings for at least some special characters. What this means is that rather than representing special characters by names or explicit hexadecimal codes, you instead represent them by raw bit patterns appropriate for a particular computer system or particular font.
| $CharacterEncoding=None | use printable ASCII names for all special characters |
| $CharacterEncoding="name" | use the raw character encoding specified by name |
| $SystemCharacterEncoding | the default raw character encoding for your particular computer system |
When you press a key or combination of keys on your keyboard, the operating system of your computer sends a certain bit pattern to the Wolfram System. How this bit pattern is interpreted as a character within the Wolfram System will depend on the character encoding that has been set up.
The notebook front end for the Wolfram System typically takes care of setting up the appropriate character encoding automatically for whatever font you are using. But if you use the Wolfram System with a text‐based interface or via files or pipes, then you may need to set $CharacterEncoding explicitly.
By specifying an appropriate value for $CharacterEncoding, you will typically be able to get the Wolfram Language to handle raw text generated by whatever language‐specific text editor or operating system you use.
You should realize, however, that while the standard representation of special characters used in the Wolfram Language is completely portable across different computer systems, any representation that involves raw character encodings will inevitably not be.
| "PrintableASCII" | printable ASCII characters only |
| "ASCII" | all ASCII including control characters |
| "ISOLatin1" | characters for common western European languages |
| "ISOLatin2" | characters for central and eastern European languages |
| "ISOLatin3" |
characters for additional European languages (e.g. Catalan, Turkish)
|
| "ISOLatin4" |
characters for other additional European languages (e.g. Estonian, Lappish)
|
| "ISOLatinCyrillic" | English and Cyrillic characters |
| "AdobeStandard" | Adobe standard PostScript font encoding |
| "MacintoshRoman" | Macintosh roman font encoding |
| "WindowsANSI" | Windows standard font encoding |
| "Symbol" | symbol font encoding |
| "ZapfDingbats" | Zapf dingbats font encoding |
| "ShiftJIS" | shift‐JIS for Japanese (mixture of 8‐ and 16‐bit) |
| "EUC" | extended Unix code for Japanese (mixture of 8‐ and 16‐bit) |
| "UTF‐8" | Unicode transformation format encoding |
The Wolfram System knows about various raw character encodings, appropriate for different computer systems and different languages. Copying of characters between the Wolfram System notebook interface and user interface environment on your computer generally uses the native character encoding for that environment. Wolfram Language characters that are not included in the native encoding will be written out using standard Wolfram Language full names or hexadecimal codes.
The Wolfram Language kernel can use any character encoding you specify when it writes or reads text files. By default, Put and PutAppend produce an ASCII representation for reliable portability of Wolfram Language files from one system to another.
The Wolfram Language supports both 8‐ and 16‐bit raw character encodings. In an encoding such as "ISOLatin1", all characters are represented by bit patterns containing 8 bits. But in an encoding such as "ShiftJIS" some characters instead involve bit patterns containing 16 bits.
Most of the raw character encodings supported by the Wolfram Language include basic ASCII as a subset. This means that even when you are using such encodings, you can still give ordinary Wolfram Language input in the usual way, and you can specify special characters using ∖[ and ∖: sequences.
Some raw character encodings, however, do not include basic ASCII as a subset. An example is the "Symbol" encoding, in which the character codes normally used for a and b are instead used for 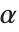 and
and 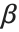 .
.
| ToCharacterCode["string"] | generate codes for characters using the standard Wolfram Language encoding |
| ToCharacterCode["string","encoding"] | generate codes for characters using the specified encoding |
| FromCharacterCode[{n1,n2,…}] | generate characters from codes using the standard Wolfram Language encoding |
| FromCharacterCode[{n1,n2,…},"encoding"] | |
generate characters from codes using the specified encoding | |
Here are the codes in the Windows standard encoding. There is no code for ∖[Pi] in that encoding:
The character codes used internally by the Wolfram Language are based on Unicode. But externally the Wolfram Language by default always uses plain ASCII sequences such as ∖[Name] or ∖:nnnn to refer to special characters. By telling it to use the "UTF-8" character encoding, however, you can get the Wolfram Language to read and write characters in a standard Unicode form.