Manipulating Equations and Inequalities
Manipulating Equations and Inequalities
"Defining Variables" discussed assignments such as x=y, which set x equal to y. Here we discuss equations, which test equality. The equation x==y tests whether x is equal to y.
It is very important that you do not confuse x=y with x==y. While x=y is an imperative statement that actually causes an assignment to be done, x==y merely tests whether x and y are equal, and causes no explicit action. If you have used the C programming language, you will recognize that the notation for assignment and testing in the Wolfram Language is the same as in C.
The tests used so far involve only numbers, and always give a definite answer, either True or False. You can also do tests on symbolic expressions.
The Wolfram Language cannot get a definite result for this test unless you give x a specific numerical value:
Even when you do tests on symbolic expressions, there are some cases where you can get definite results. An important one is when you test the equality of two expressions that are identical. Whatever the numerical values of the variables in these expressions may be, the Wolfram Language knows that the expressions must always be equal.
The Wolfram Language does not try to tell whether these expressions are equal. In this case, using Expand would make them have the same form:
Expressions like x==4 represent equations in the Wolfram Language. There are many functions in the Wolfram Language for manipulating and solving equations.
An expression like x^2+2x-7==0 represents an equation in the Wolfram Language. You will often need to solve equations like this, to find out for what values of x they are true.
This gives the two solutions to the quadratic equation 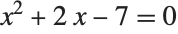 . The solutions are given as replacements for x:
. The solutions are given as replacements for x:
You can get a list of the actual solutions for x by applying the rules generated by Solve to x using the replacement operator:
| Solve[lhs==rhs,x] |
solve an equation, giving a list of rules for
x
|
| x/.solution | use the list of rules to get values for x |
| expr/.solution | use the list of rules to get values for an expression |
Solve always tries to give you explicit formulas for the solutions to equations. However, it is a basic mathematical result that, for sufficiently complicated equations, explicit algebraic formulas in terms of radicals cannot be given. If you have an algebraic equation in one variable, and the highest power of the variable is at most four, then the Wolfram Language can always give you formulas for the solutions. However, if the highest power is five or more, it may be mathematically impossible to give explicit algebraic formulas for all the solutions.
The Wolfram Language can always solve algebraic equations in one variable when the highest power is less than five:
There are some equations, however, for which it is mathematically impossible to find explicit formulas for the solutions. The Wolfram Language uses Root objects to represent the solutions in this case:
In addition to being able to solve purely algebraic equations, the Wolfram Language can also solve some equations involving other functions.
It is important to realize that an equation such as  actually has an infinite number of possible solutions. However, Solve by default returns just one solution, but prints a message telling you that other solutions may exist. You can use Reduce to get more information.
actually has an infinite number of possible solutions. However, Solve by default returns just one solution, but prints a message telling you that other solutions may exist. You can use Reduce to get more information.
Solve can also handle equations involving symbolic functions. In such cases, it again prints a warning, then gives results in terms of formal inverse functions.
| Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
solve a set of simultaneous equations for x, y, … | |
You can also use the Wolfram Language to solve sets of simultaneous equations. You simply give the list of equations and specify the list of variables to solve for.
Here are some more complicated simultaneous equations. The two solutions are given as two lists of replacements for x and y:
When you are working with sets of equations in several variables, it is often convenient to reorganize the equations by eliminating some variables between them.
If you have several equations, there is no guarantee that there exists any consistent solution for a particular variable.
There is no consistent solution to these equations, so the Wolfram Language returns {}, indicating that the set of solutions is empty:
The general question of whether a set of equations has any consistent solution is quite a subtle one. For example, for most values of a, the equations {x==1,x==a} are inconsistent, so there is no possible solution for x. However, if a is equal to 1, then the equations do have a solution. Solve is set up to give you generic solutions to equations. It discards any solutions that exist only when special constraints between parameters are satisfied.
If you use Reduce instead of Solve, the Wolfram Language will, however, keep all the possible solutions to a set of equations, including those that require special conditions on parameters.
This shows that the equations have a solution only when a==1. The notation a==1&&x==1 represents the requirement that both a==1 and x==1 should be True:
This gives the complete set of possible solutions to the equation. The answer is stated in terms of a combination of simpler equations. && indicates equations that must simultaneously be true; || indicates alternatives:
| Solve[lhs==rhs,x] | solve an equation for x |
| Solve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
solve a set of simultaneous equations for x, y, … | |
| Eliminate[{lhs1==rhs1,lhs2==rhs2,…},{x,…}] | |
eliminate x, … in a set of simultaneous equations | |
| Reduce[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
give a set of simplified equations, including all possible solutions
| |
Reduce also has powerful capabilities for handling equations specifically over real numbers or integers. "Equations and Inequalities over Domains" discusses this in more detail.
The Wolfram System treats equations as logical statements. If you type in an equation like x^2+3x==2, the Wolfram System interprets this as a logical statement that asserts that x^2+3x is equal to 2. If you have assigned an explicit value to x, say x=4, then the Wolfram System can explicitly determine that the logical statement x^2+3x==2 is False.
If you have not assigned any explicit value to x, however, the Wolfram System cannot work out whether x^2+3x==2 is True or False. As a result, it leaves the equation in the symbolic form x^2+3x==2.
You can manipulate symbolic equations in the Wolfram System in many ways. One common goal is to rearrange the equations so as to "solve" for a particular set of variables.
You can use the function Reduce to reduce the equation so as to give "solutions" for x. The result, like the original equation, can be viewed as a logical statement:
The quadratic equation x^2+3x==2 can be thought of as an implicit statement about the value of x. As shown in the previous example, you can use the function Reduce to get a more explicit statement about the value of x. The expression produced by Reduce has the form x==r1||x==r2. This expression is again a logical statement, which asserts that either x is equal to r1, or x is equal to r2. The values of x that are consistent with this statement are exactly the same as the ones that are consistent with the original quadratic equation. For many purposes, however, the form that Reduce gives is much more useful than the original equation.
You can combine and manipulate equations just like other logical statements. You can use logical connectives such as || and && to specify alternative or simultaneous conditions. You can use functions like LogicalExpand, as well as FullSimplify, to simplify collections of equations.
For many purposes, you will find it convenient to manipulate equations simply as logical statements. Sometimes, however, you will actually want to use explicit solutions to equations in other calculations. In such cases, it is convenient to convert equations that are stated in the form lhs==rhs into transformation rules of the form lhsrhs. Once you have the solutions to an equation in the form of explicit transformation rules, you can substitute the solutions into expressions by using the /. operator.
Reduce produces a logical statement about the values of x corresponding to the roots of the quadratic equation:
ToRules converts the logical statement into an explicit list of transformation rules:
You can now use the transformation rules to substitute the solutions for x into expressions involving x:
The function Solve produces transformation rules for solutions directly:
The main equations that Solve and related Wolfram Language functions deal with are polynomial equations.
The Wolfram Language can also find exact solutions to cubic equations. Here is the first solution to a comparatively simple cubic equation:
For cubic and quartic equations, the results are often complicated, but for all equations with degrees up to four the Wolfram Language is always able to give explicit formulas for the solutions.
An important feature of these formulas is that they involve only radicals: arithmetic combinations of square roots, cube roots and higher roots.
It is a fundamental mathematical fact, however, that for equations of degree five or higher, it is no longer possible in general to give explicit formulas for solutions in terms of radicals.
There are some specific equations for which this is still possible, but in the vast majority of cases it is not.
For a polynomial that factors in the way this one does, it is straightforward for Solve to find the roots:
The polynomial does not factor, but it can be decomposed into nested polynomials, so Solve can again find explicit formulas for the roots:
| Root[f,k] | the k th root of the equation f[x]==0 |
No explicit formulas for the solution to this equation can be given in terms of radicals, so the Wolfram Language uses an implicit symbolic representation:
If what you want in the end is a numerical solution, it is usually much faster to use NSolve from the outset:
Root objects provide an exact, though implicit, representation for the roots of a polynomial. You can work with them much as you would work with Sqrt[2] or any other expression that represents an exact numerical quantity.
Here is the Root object representing the first root of the polynomial discussed previously:
Round does an exact computation to find the closest integer to the root:
If you substitute the root into the original polynomial, and then simplify the result, you get zero:
If the only symbolic parameter that exists in an equation is the variable that you are solving for, then all the solutions to the equation will just be numbers. But if there are other symbolic parameters in the equation, then the solutions will typically be functions of these parameters.
The solution to this equation can again be represented by Root objects, but now each Root object involves the parameter a:
When a is replaced with 1, the Root objects can be simplified, and some are given as explicit radicals:
If you give Solve any 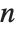 th‐degree polynomial equation, then it will always return exactly
th‐degree polynomial equation, then it will always return exactly 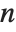 solutions, although some of these may be represented by Root objects. If there are degenerate solutions, then the number of times that each particular solution appears will be equal to its multiplicity.
solutions, although some of these may be represented by Root objects. If there are degenerate solutions, then the number of times that each particular solution appears will be equal to its multiplicity.
Solve gives two identical solutions to this equation:
The Wolfram Language also knows how to solve equations that are not explicitly in the form of polynomials.
So long as it can reduce an equation to some kind of polynomial form, the Wolfram Language will always be able to represent its solution in terms of Root objects. However, with more general equations, involving, say, transcendental functions, there is no systematic way to use Root objects, or even necessarily to find numerical approximations.
Polynomial equations in one variable only ever have a finite number of solutions. But transcendental equations often have an infinite number. Typically the reason for this is that transcendental functions in effect have infinitely many possible inverses. With the default option setting InverseFunctionsTrue, Solve will nevertheless assume that there is a definite inverse for any such function. Solve may then be able to return particular solutions in terms of this inverse function.
The Wolfram Language returns a particular solution in terms of ProductLog, but prints a warning indicating that other solutions may be lost:
If you ask Solve to solve an equation involving an arbitrary function like f, it will by default try to construct a formal solution in terms of inverse functions.
| InverseFunction[f] | the inverse function of f |
| InverseFunction[f,k,n] | the inverse function of the n‐argument function f with respect to its k th argument |
While Solve can only give specific solutions to an equation, Reduce can give a representation of a whole solution set. For transcendental equations, it often ends up introducing new parameters, say with values ranging over all possible integers.
As discussed at more length in "Equations and Inequalities over Domains", Reduce allows you to restrict the domains of variables. Sometimes this will let you generate definite solutions to transcendental equations—or show that they do not exist.
Reduce knows there can be no solution here:
Counting Roots of Polynomials
| CountRoots[poly,x] | give the number of real roots of the polynomial poly in x |
| CountRoots[poly,{x,a,b}] | give the number of roots of the polynomial poly in x with |
CountRoots accepts polynomials with Gaussian rational coefficients. The root count includes multiplicities.
The roots of 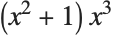 in the vertical axis segment between
in the vertical axis segment between 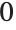 and
and 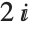 consist of a triple root at
consist of a triple root at 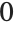 and a single root at
and a single root at 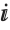 :
:
Isolating Intervals
A set  , where
, where 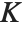 is
is  or
or  , is an isolating set for a root
, is an isolating set for a root 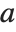 of a polynomial
of a polynomial 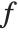 if
if 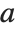 is the only root of
is the only root of 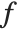 in
in 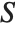 . Isolating roots of a polynomial means finding disjoint isolating sets for all the roots of the polynomial.
. Isolating roots of a polynomial means finding disjoint isolating sets for all the roots of the polynomial.
| RootIntervals[{poly1,poly2,…}] | give a list of disjoint isolating intervals for the real roots of any of the polyi, together with a list of which polynomials actually have each successive root |
| RootIntervals[poly] | give disjoint isolating intervals for real roots of a single polynomial |
| RootIntervals[polys,Complexes] | give disjoint isolating intervals or rectangles for complex roots of polys |
| IsolatingInterval[a] | give an isolating interval for the algebraic number a |
| IsolatingInterval[a,dx] | give an isolating interval of width at most dx |
RootIntervals accepts polynomials with rational number coefficients.
For a real root 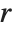 , the returned isolating interval is a pair of rational numbers
, the returned isolating interval is a pair of rational numbers 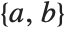 , such that either
, such that either 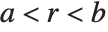 or
or 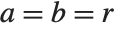 . For a nonreal root
. For a nonreal root 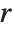 , the isolating rectangle returned is a pair of Gaussian rational numbers
, the isolating rectangle returned is a pair of Gaussian rational numbers 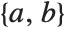 such that
such that 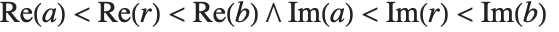 and either
and either 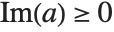 or
or  .
.
Here are isolating intervals for the third- and fourth-degree roots of unity. The second interval contains a root common to both polynomials:
| Root[f,k] | the k th root of the polynomial equation f[x]==0 |
When you enter a Root object, the polynomial that appears in it is automatically reduced to a minimal form:
Root objects are the way that the Wolfram Language represents algebraic numbers. Algebraic numbers have the property that when you perform algebraic operations on them, you always get a single algebraic number as the result.
Again this can be reduced to a single Root object, albeit a fairly complicated one:
| RootReduce[expr] | attempt to reduce expr to a single Root object |
| ToRadicals[expr] | attempt to transform Root objects to explicit radicals |
In this simple case, the Root object is automatically expressed in terms of radicals:
When cubic polynomials are involved, Root objects are not automatically expressed in terms of radicals:
If Solve and ToRadicals do not succeed in expressing the solution to a particular polynomial equation in terms of radicals, then it is a good guess that this fundamentally cannot be done. However, you should realize that there are some special cases in which a reduction to radicals is in principle possible, but the Wolfram System cannot find it. The simplest example is the equation 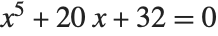 , but here the solution in terms of radicals is very complicated. The equation
, but here the solution in terms of radicals is very complicated. The equation 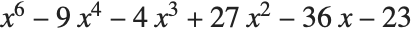 is another example, where now
is another example, where now 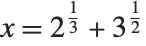 is a solution.
is a solution.
This gives a Root object involving a degree-six polynomial:
Even though a simple form in terms of radicals does exist, ToRadicals does not find it:
Beyond degree four, most polynomials do not have roots that can be expressed at all in terms of radicals. However, for degree five it turns out that the roots can always be expressed in terms of elliptic or hypergeometric functions. The results, however, are typically much too complicated to be useful in practice.
| RootApproximant[x] | converts the number x to one of the "simplest" algebraic numbers that approximates it well |
| RootApproximant[x,n] | finds an algebraic number of degree at most n that approximates x |
You can give Solve a list of simultaneous equations to solve. Solve can find explicit solutions for a large class of simultaneous polynomial equations.
Here is a more complicated example. The result is a list of solutions, with each solution consisting of a list of transformation rules for the variables:
Even when Solve cannot find explicit solutions, it often can "unwind" simultaneous equations to produce a symbolic result in terms of Root objects:
You can then use N to get a numerical result:
The variables that you use in Solve do not need to be single symbols. Often when you set up large collections of simultaneous equations, you will want to use expressions like a[i] as variables.
| Solve[eqns,{x1,x2,…}] | solve eqns for the specific objects xi |
| Solve[eqns] | try to solve eqns for all the objects that appear in them |
If you do not explicitly specify objects to solve for, Solve will try to solve for all the variables:
| ■ Solve[{lhs1==rhs1,lhs2==rhs2,…},vars] |
| ■ Solve[lhs1==rhs1&&lhs2==rhs2&&…,vars] |
| ■ Solve[{lhs1,lhs2,…}=={rhs1,rhs2,…},vars] |
Ways to present simultaneous equations to Solve.
If you construct simultaneous equations from matrices, you typically get equations between lists of expressions:
Solve converts equations involving lists to lists of equations:
You can use LogicalExpand to do the conversion explicitly:
In some kinds of computations, it is convenient to work with arrays of coefficients instead of explicit equations. You can construct such arrays from equations by using CoefficientArrays.
If you have an equation like 2x==0, it is perfectly clear that the only possible solution is x0. However, if you have an equation like ax==0, things are not so clear. If a is not equal to zero, then x0 is again the only solution. However, if a is in fact equal to zero, then any value of x is a solution. You can see this by using Reduce.
Reduce, on the other hand, gives you all the possibilities, without assuming anything about the value of a:
A basic difference between Reduce and Solve is that Reduce gives all the possible solutions to a set of equations, while Solve gives only the generic ones. Solutions are considered "generic" if they involve conditions only on the variables that you explicitly solve for, and not on other parameters in the equations. Reduce and Solve also differ in that Reduce always returns combinations of equations, while Solve gives results in the form of transformation rules.
| Solve[eqns,vars] | find generic solutions to equations |
| Reduce[eqns,vars] |
reduce equations, maintaining all solutions
|
This is the solution to an arbitrary linear equation given by Solve:
Reduce gives the full version, which includes the possibility a==b==0. In reading the output, note that && has higher precedence than ||:
Here is the full solution to a general quadratic equation. There are three alternatives. If a is nonzero, then there are two solutions for x, given by the standard quadratic formula. If a is zero, however, the equation reduces to a linear one. Finally, if a, b and c are all zero, there is no restriction on x:
When you have several simultaneous equations, Reduce can show you under what conditions the equations have solutions. Solve shows you whether there are any generic solutions.
The solution is not generic, and is rejected by Solve:
This is the kind of result Solve returns when you give an equation that is always true:
When you work with systems of linear equations, you can use Solve to get generic solutions and Reduce to find out for what values of parameters solutions exist.
Solve reports that there are no generic solutions:
Reduce, however, shows that there would be a solution if the parameters satisfied the special condition a==2b-c:
For nonlinear equations, the conditions for the existence of solutions can be much more complicated.
Solve shows that the equations have no generic solutions:
Reduce gives the complete conditions for a solution to exist:
When you write down a set of simultaneous equations in the Wolfram Language, you are specifying a collection of constraints between variables. When you use Solve, you are finding values for some of the variables in terms of others, subject to the constraints represented by the equations.
| Solve[eqns,vars,elims] | find solutions for vars, eliminating the variables elims |
| Eliminate[eqns,elims] | rearrange equations to eliminate the variables elims |
If you only want to solve for x, however, you have to specify whether you want to eliminate y or a or b. This eliminates y, and so gives the result in terms of a and b:
In some cases, you may want to construct explicitly equations in which variables have been eliminated. You can do this using Eliminate.
As a more sophisticated example of Eliminate, consider the problem of writing 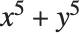 in terms of the "symmetric polynomials"
in terms of the "symmetric polynomials"  and
and 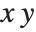 .
.
To solve the problem, simply write f in terms of a and b, eliminating the original variables x and y:
In dealing with sets of equations, it is common to consider some of the objects that appear as true "variables", and others as "parameters". In some cases, you may need to know for what values of parameters a particular relation between the variables is always satisfied.
| SolveAlways[eqns,vars] | solve for the values of parameters for which the eqns are satisfied for all values of the vars |
| x==y |
equal (also input as
xy
)
|
| x!=y |
unequal (also input as
x≠y
)
|
| x>y | greater than |
| x>=y |
greater than or equal to (also input as
x≥y
)
|
| x<y | less than |
| x<=y |
less than or equal to (also input as
x≤y
)
|
| x==y==z | all equal |
| x!=y!=z |
all unequal (distinct)
|
| x>y>z
, etc.
|
strictly decreasing, etc.
|
Not all of these numbers are unequal, so this gives False:
Since both of the quantities involved are numeric, the Wolfram Language can determine that this is true:
| !p |
not (also input as
¬
p
)
|
| p&&q&&… |
and (also input as
p∧q∧…
)
|
| p||q||… |
or (also input as
p∨q∨…
)
|
| Xor[p,q,…] |
exclusive or (also input as
p⊻q⊻…
)
|
| Nand[p,q,…] and Nor[p,q,…] | nand and nor (also input as ⊼ and ⊽) |
| If[p,then,else] | |
| LogicalExpand[expr] | expand out logical expressions |
You should remember that the logical operations ==, && and || are all double characters in the Wolfram Language. If you have used a programming language such as C, you will be familiar with this notation.
You can use LogicalExpand to expand out the terms:
When you give a list of equations to Solve, it assumes that you want all the equations to be satisfied simultaneously. It is also possible to give Solve more complicated logical combinations of equations.
This specifies that either x+y==1 or x-y==2. Solve gives two solutions for x, corresponding to these two possibilities:
Solve gives three solutions to this equation:
Here is a slightly more complicated example. Note that the precedence of || is lower than the precedence of &&, so the equation is interpreted as (x^3==x&&x!=1)||x^2==2, not x^3==x&&(x!=1||x^2==2):
When you use Solve, the final results you get are in the form of transformation rules. If you use Reduce or Eliminate, on the other hand, then your results are logical statements, which you can manipulate further.
This finds values of x that satisfy x^5==x but do not satisfy the statement representing the solutions of x^2==x:
The logical statements produced by Reduce can be thought of as representations of the solution set for your equations. The logical connectives &&, || and so on then correspond to operations on these sets.
| eqns1||eqns2 | union of solution sets |
| eqns1&&eqns2 | intersection of solution sets |
| !eqns | complement of a solution set |
| Implies[eqns1,eqns2] | the part of eqns1 that contains eqns2 |
You may often find it convenient to use special notations for logical connectives, as discussed in "Operators".
Just as the equation x^2+3x==2 asserts that x^2+3x is equal to 2, so also the inequality x^2+3x>2 asserts that x^2+3x is greater than 2. In the Wolfram Language, Reduce works not only on equations, but also on inequalities.
| Reduce[{ineq1,ineq2,…},x] | reduce a collection of inequalities in x |
When applied to an equation, Reduce[eqn,x] tries to get a result consisting of simple equations for x of the form x==r1, …. When applied to an inequality, Reduce[ineq,x] does the exactly analogous thing, and tries to get a result consisting of simple inequalities for x of the form l1<x<r1, ….
You can think of the result generated by Reduce[ineq,x] as representing a series of intervals, described by inequalities. Since the graph of a polynomial of degree 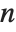 can go up and down as many as
can go up and down as many as 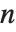 times, a polynomial inequality of degree
times, a polynomial inequality of degree 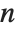 can give rise to as many as
can give rise to as many as 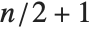 distinct intervals.
distinct intervals.
Solving this inequality requires introducing ProductLog:
Transcendental functions like 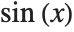 have graphs that go up and down infinitely many times, so that infinitely many intervals can be generated.
have graphs that go up and down infinitely many times, so that infinitely many intervals can be generated.
This is how Reduce represents infinitely many intervals:
If you have inequalities that involve <= as well as <, there may be isolated points where the inequalities can be satisfied. Reduce represents such points by giving equations.
| Reduce[{ineq1,ineq2,…},{x1
,
x2
,
…
}]
| reduce a collection of inequalities in several variables |
For inequalities involving several variables, Reduce in effect yields nested collections of interval specifications, in which later variables have bounds that depend on earlier variables.
In geometrical terms, any linear inequality divides space into two halves. Lists of linear inequalities thus define polyhedra, sometimes bounded, sometimes not. Reduce represents such polyhedra in terms of nested inequalities. The corners of the polyhedra always appear among the endpoints of these inequalities.
Lists of inequalities in general represent regions of overlap between geometrical objects. Often the description of these can be quite complicated.
If you have inequalities that involve parameters, Reduce automatically handles the different cases that can occur, just as it does for equations.
Reduce tries to give you a complete description of the region defined by a set of inequalities. Sometimes, however, you may just want to find individual instances of values of variables that satisfy the inequalities. You can do this using FindInstance.
| FindInstance[ineqs,{x1,x2,…}] | try to find an instance of the xi satisfying ineqs |
| FindInstance[ineqs,vars,n] | try to find n instances |
FindInstance is in some ways an analog for inequalities of Solve for equations. Like Solve, it returns a list of rules giving specific values for variables. But while for equations these values can generically give an accurate representation of all solutions, for inequalities they can only correspond to isolated sample points within the regions described by the inequalities.
Every time you call FindInstance with specific input, it will give the same output. And when there are instances that correspond to special, limiting points of some kind, it will preferentially return these. But in general, the distribution of instances returned by FindInstance will typically seem somewhat random. Each instance is, however, in effect a constructive proof that the inequalities you have given can in fact be satisfied.
If you ask for one point in the unit disk, FindInstance gives the origin:
The Wolfram Language normally assumes that variables that appear in equations can stand for arbitrary complex numbers. But when you use Reduce, you can explicitly tell the Wolfram Language that the variables stand for objects in more restricted domains.
| Reduce[expr,vars,dom] | reduce eqns over the domain dom |
| Complexes | complex numbers |
| Reals | real numbers |
| Integers | integers |
A single polynomial equation in one variable will always have a finite set of discrete solutions. And in such a case, one can think of Reduce[eqns,vars,dom] as just filtering the solutions by selecting the ones that happen to lie in the domain dom.
But as soon as there are more variables, things can become more complicated, with solutions to equations corresponding to parametric curves or surfaces in which the values of some variables can depend on the values of others. Often this dependence can be described by some collection of equations or inequalities, but the form of these can change significantly when one goes from one domain to another.
If your input involves only equations, then Reduce will by default assume that all variables are complex. But if your input involves inequalities, then Reduce will assume that any algebraic variables appearing in them are real, since inequalities can only compare real quantities.
For systems of polynomials over real and complex domains, the solutions always consist of a finite number of components, within which the values of variables are given by algebraic numbers or functions.
While in principle Reduce can always find the complete solution to any collection of polynomial equations and inequalities with real or complex variables, the results are often very complicated, with the number of components typically growing exponentially as the number of variables increases.
As soon as one introduces functions like Sin or Exp, even equations in single real or complex variables can have solutions with an infinite number of components. Reduce labels these components by introducing additional parameters. By default, the 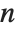 th parameter in a given solution will be named C[n]. In general, you can specify that it should be named f[n] by giving the option setting GeneratedParameters->f.
th parameter in a given solution will be named C[n]. In general, you can specify that it should be named f[n] by giving the option setting GeneratedParameters->f.
Reduce can handle equations not only over real and complex variables, but also over integers. Solving such Diophantine equations can often be a very difficult problem.
Reduce can solve any system of linear equations or inequalities over the integers. With 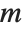 linear equations in
linear equations in 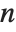 variables,
variables,  parameters typically need to be introduced. But with inequalities, a much larger number of parameters may be needed.
parameters typically need to be introduced. But with inequalities, a much larger number of parameters may be needed.
With two variables, Reduce can solve any quadratic equation over the integers. The result can be a Fibonacci‐like sequence, represented in terms of powers of quadratic irrationals.
The actual values for specific C[1] as integers, as they should be:
Reduce can handle many specific classes of equations over the integers.
Here Reduce finds the solution to a Thue equation:
Equations over the integers sometimes have seemingly quite random collections of solutions. And even small changes in equations can often lead them to have no solutions at all.
For polynomial equations over real and complex numbers, there is a definite decision procedure for determining whether or not any solution exists. But for polynomial equations over the integers, the unsolvability of Hilbert's tenth problem demonstrates that there can never be any such general procedure.
For specific classes of equations, however, procedures can be found, and indeed many are implemented in Reduce. But handling different classes of equations can often seem to require whole different branches of number theory, and quite different kinds of computations. And in fact it is known that there are universal integer polynomial equations, for which filling in some variables can make solutions for other variables correspond to the output of absolutely any possible program. This then means that for such equations there can never in general be any closed‐form solution built from fixed elements like algebraic functions.
If one includes functions like Sin, then even for equations involving real and complex numbers the same issues can arise.
Reduce here effectively has to solve an equation over the integers:
Since there are only ever a finite number of possible solutions for integer equations modulo n, Reduce can systematically find them.
Reduce can also handle equations that involve several different moduli.
| Reduce[expr,vars,dom] | specify a default domain for all variables |
| Reduce[{expr1,…,x1∈dom1,…},vars] | explicitly specify individual domains for variables |
Reduce normally treats complex variables as single objects. But in dealing with functions that are not analytic or have branch cuts, it sometimes has to break them into pairs of real variables Re[z] and Im[z].
Reduce by default assumes that variables that appear algebraically in inequalities are real. But you can override this by explicitly specifying Complexes as the default domain. It is often useful in such cases to be able to specify that certain variables are still real.
| FindInstance[expr,{x1,x2,…},dom] | try to find an instance of the xi in dom satisfying expr |
| FindInstance[expr,vars,dom,n] | try to find n instances |
| Complexes | the domain of complex numbers |
| Reals | the domain of real numbers |
| Integers | the domain of integers |
| Booleans |
Reduce always returns a complete representation of the solution to a system of equations or inequalities. Sometimes, however, you may just want to find particular sample solutions. You can do this using FindInstance.
If FindInstance[expr,vars,dom] returns {} then this means that the Wolfram Language has effectively proved that expr cannot be satisfied for any values of variables in the specified domain. When expr can be satisfied, FindInstance will normally pick quite arbitrarily among values that do this, as discussed for inequalities in "Inequalities: Manipulating Equations and Inequalities".
Particularly for integer equations, FindInstance can often find particular solutions to equations even when Reduce cannot find a complete solution. In such cases it usually returns one of the smallest solutions to the equations.
One feature of FindInstance is that it also works with Boolean expressions whose variables can have values True or False. You can use FindInstance to determine whether a particular expression is satisfiable, so that there is some choice of truth values for its variables that makes the expression True.
Any combination of equations or inequalities can be thought of as implicitly defining a region in some kind of space. The fundamental function of Reduce is to turn this type of implicit description into an explicit one.
An implicit description in terms of equations or inequalities is sufficient if you just want to test whether a point specified by values of variables is in the region. But to understand the structure of the region, or to generate points in it, you typically need a more explicit description, of the kind obtained from Reduce.
Reduce gives a more explicit representation of the region:
If you pick a value for x consistent with the first inequality, you then immediately get an explicit inequality for y:
Reduce[expr,{x1,x2,…}] is set up to describe regions by first giving fixed conditions for x1, then giving conditions for x2 that depend on x1, then conditions for x3 that depend on x1 and x2 and so on. This structure has the feature that it allows you to pick points by successively choosing values for each of the xi in turn—in much the same way as when you uses iterators in functions like Table.
In some simple cases, the region defined by a system of equations or inequalities will end up having only one component. In such cases, the output from Reduce will be of the form e1&&e2…, where each of the ei is an equation or inequality involving variables up to xi.
In most cases, however, there will be several components, represented by output containing forms such as u1||u2||…. Reduce typically tries to minimize the number of components used in describing a region. But in some cases, multiple parametrizations may be needed to cover a single connected component, and each one of these will appear as a separate component in the output from Reduce.
In representing solution sets, it is common to find that several components can be described together by using forms such as …&&(u1||u2)&&…. Reduce by default does this so as to return its results as compactly as possible. You can use LogicalExpand to generate an expanded form in which each component appears separately.
In generating the most compact results, Reduce sometimes ends up making conditions on later variables xi depend on more of the earlier xi than is strictly necessary. You can force Reduce to generate results in which a particular xi only has minimal dependence on earlier xi by giving the option BacksubstitutionTrue. Usually this will lead to much larger output, although sometimes it may be easier to interpret.
| CylindricalDecomposition[expr,{x1,x2,…}] | |
generate the cylindrical algebraic decomposition of the region defined by expr | |
| GenericCylindricalDecomposition[expr,{x1,x2,…}] | |
find the full-dimensional part of the decomposition of the region defined by expr, together with any hypersurfaces containing the rest of the region | |
| SemialgebraicComponentInstances[expr,{x1,x2,…}] | |
give at least one point in each connected component of the region defined by expr | |
For polynomial equations or inequalities over the reals, the structure of the result returned by Reduce is typically a cylindrical algebraic decomposition or CAD. Sometimes Reduce can yield a simpler form. But in all cases, you can get the complete CAD by using CylindricalDecomposition. For systems containing inequalities only, GenericCylindricalDecomposition gives you "most" of the solution set and is often faster.
In a statement like x^4+x^2>0, the Wolfram Language treats the variable x as having a definite, though unspecified, value. Sometimes, however, it is useful to be able to make statements about whole collections of possible values for x. You can do this using quantifiers.
| ForAll[x,expr] | expr holds for all values of x |
| ForAll[{x1,x2,…},expr] | expr holds for all values of all the xi |
| ForAll[{x1,x2,…},cond,expr] | expr holds for all xisatisfying cond |
| Exists[x,expr] | there exists a value of x for which expr holds |
| Exists[{x1,x2,…},expr] | there exist values of the xi for which expr holds |
| Exists[{x1,…},cond,expr] | there exist values of the xi satisfying cond for which expr holds |
You can work with quantifiers in the Wolfram Language much as you work with equations, inequalities or logical connectives. In most cases, the quantifiers will not immediately be changed by evaluation. But they can be simplified or reduced by functions like FullSimplify and Reduce.
This asserts that an x exists that makes the inequality true. The output here is just a formatted version of the input:
FullSimplify establishes that the assertion is true:
The Wolfram Language supports a version of the standard notation for quantifiers used in predicate logic and pure mathematics. You can input  as \[ForAll] or EscfaEsc, and you can input
as \[ForAll] or EscfaEsc, and you can input 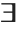 as \[Exists] or EscexEsc. To make the notation precise, however, the Wolfram Language makes the quantified variable a subscript. The conditions on the variable can also be given in the subscript, separated by a comma.
as \[Exists] or EscexEsc. To make the notation precise, however, the Wolfram Language makes the quantified variable a subscript. The conditions on the variable can also be given in the subscript, separated by a comma.
| ∀xexpr | ForAll[x,expr] |
| ∀{x1,x2,…}expr | ForAll[{x1,x2,…},expr] |
| ∀x,condexpr | ForAll[x,cond,expr] |
| ∃xexpr | Exists[x,expr] |
| ∃{x1,x2,…}expr | Exists[{x1,x2,…},expr] |
| ∃x,condexpr | Exists[x,cond,expr] |
Given a statement that involves quantifiers, there are certain important cases where it is possible to resolve it into an equivalent statement in which the quantifiers have been eliminated. Somewhat like solving an equation, such quantifier elimination turns an implicit statement about what is true for all x or for some x into an explicit statement about the conditions under which this holds.
| Resolve[expr] | attempt to eliminate quantifiers from expr |
| Resolve[expr,dom] | attempt to eliminate quantifiers with all variables assumed to be in domain dom |
Resolve can always eliminate quantifiers from any collection of polynomial equations and inequations over complex numbers, and from any collection of polynomial equations and inequalities over real numbers. It can also eliminate quantifiers from Boolean expressions.
You can also use quantifiers with Reduce. If you give Reduce a collection of equations or inequalities, then it will try to produce a detailed representation of the complete solution set. But sometimes you may want to address a more global question, such as whether the solution set covers all values of x, or whether it covers none of these values. Quantifiers provide a convenient way to specify such questions.
Although quantifier elimination over the integers is in general a computationally impossible problem, the Wolfram Language can do it in specific cases.
| Minimize[expr,{x1,x2,…}] | minimize expr |
| Minimize[{expr,cons},{x1,x2,…}] | minimize expr subject to the constraints cons |
| Maximize[expr,{x1,x2,…}] | maximize expr |
| Maximize[{expr,cons},{x1,x2,…}] | maximize expr subject to the constraints cons |
Minimize and Maximize yield lists giving the value attained at the minimum or maximum, together with rules specifying where the minimum or maximum occurs.
Minimize[expr,x] minimizes expr allowing x to range over all possible values from  to
to  . Minimize[{expr,cons},x] minimizes expr subject to the constraints cons being satisfied. The constraints can consist of any combination of equations and inequalities.
. Minimize[{expr,cons},x] minimizes expr subject to the constraints cons being satisfied. The constraints can consist of any combination of equations and inequalities.
Minimize and Maximize can solve any linear programming problem in which both the objective function expr and the constraints cons involve the variables 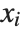 only linearly.
only linearly.
They can also in principle solve any polynomial programming problem in which the objective function and the constraints involve arbitrary polynomial functions of the variables. There are many important geometrical and other problems that can be formulated in this way.
This solves the simple geometrical problem of maximizing the area of a rectangle with fixed perimeter:
An important feature of Minimize and Maximize is that they always find global minima and maxima. Often functions will have various local minima and maxima at which derivatives vanish. But Minimize and Maximize use global methods to find absolute minima or maxima, not just local extrema.
Maximize finds the global maximum:
If you give functions that are unbounded, Minimize and Maximize will return  and
and  as the minima and maxima. And if you give constraints that can never be satisfied, they will return
as the minima and maxima. And if you give constraints that can never be satisfied, they will return  and
and  as the minima and maxima, and Indeterminate as the values of variables.
as the minima and maxima, and Indeterminate as the values of variables.
One subtle issue is that Minimize and Maximize allow both nonstrict inequalities of the form  , and strict ones of the form
, and strict ones of the form  . With nonstrict inequalities there is no problem with a minimum or maximum lying exactly on the boundary
. With nonstrict inequalities there is no problem with a minimum or maximum lying exactly on the boundary  . But with strict inequalities, a minimum or maximum must in principle be at least infinitesimally inside the boundary.
. But with strict inequalities, a minimum or maximum must in principle be at least infinitesimally inside the boundary.
With a strict inequality, the Wolfram Language prints a warning, then returns the point on the boundary:
Minimize and Maximize normally assume that all variables you give are real. But by giving a constraint such as x∈Integers you can specify that a variable must in fact be an integer.
Minimize and Maximize can compute maxima and minima of linear functions over the integers in bounded polyhedra. This is known as integer linear programming.
Minimize and Maximize can produce exact symbolic results for polynomial optimization problems with parameters.
| MinValue[{f,cons},{x,y,…}] | give the minimum value of f subject to the constraints cons |
| MaxValue[{f,cons},{x,y,…}] | give the maximum value of f subject to the constraints cons |
| ArgMin[{f,cons},{x,y,…}] | give a position at which f is minimized subject to the constraints cons |
| ArgMax[{f,cons},{x,y,…}] | give a position at which f is maximized subject to the constraints cons |
Maximize gives both the value and the position of a maximum:
Use MaxValue if you only need the maximum value:
ArgMax gives a position at which the maximum value is attained: