Search for all pages containing D






D 
Details and Options



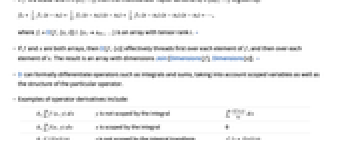
- D is also known as derivative for univariate functions.
- By using the character ∂, entered as
 pd
pd or \[PartialD], with subscripts, derivatives can be entered as follows:
or \[PartialD], with subscripts, derivatives can be entered as follows: -
D[f,x] ∂xf D[f,{x,n}] ∂{x,n}f D[f,x,y] ∂x,yf D[f,{{x,y}}] ∂{{x,y}}f - The comma can be made invisible by using the character \[InvisibleComma] or
 ,
, .
. - The partial derivative D[f[x],x] is defined as
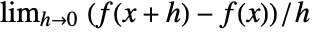 , and higher derivatives D[f[x,y],x,y] are defined recursively as
, and higher derivatives D[f[x,y],x,y] are defined recursively as 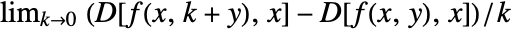 etc.
etc. - The order of derivatives n and m can be symbolic and they are assumed to be positive integers.
- The derivative D[f[x],{x,n}] for a symbolic f is represented as Derivative[n][f][x].
- For some functions f, Derivative[n][f][x] may not be known, but can be approximated by applying N. »
- New derivative rules can be added by adding values to Derivative[n][f][x]. »
- For lists, D[{f1,f2,…},x] is equivalent to {D[f1,x],D[f2,x],…} recursively. »
- D[f,{array}] effectively threads D over each element of array.
- D[f,{array,n}] is equivalent to D[f,{array},{array},…], where {array} is repeated n times.
- D[f,{array1},{array2},…] is normally equivalent to First[Outer[D,{f},array1,array2,…]]. »
- Common array derivatives include:
-
D[f,{{x1,x2,…}}] gradient {D[f,x1],D[f,x2],…} D[f,{{x1,x2,…},2}] Hessian {{D[f,x1,x1],D[f,x1,x2],…},{D[f,x2,x1],D[f,x2,x2],…},…} D[{f1,f2,…},{{x1,x2,…}}] Jacobian {{D[f1,x1],D[f1,x2],…},
{D[f2,x1],D[f2,x2],…},…} - If f is a scalar and x={x1,…}, then the multivariate Taylor series at x0={x01,…} is given by:
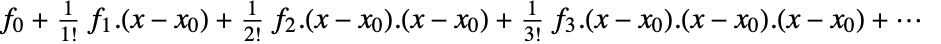 ,
,- where fi=D[f,{x,i}]/.{x1x01,…} is an array with tensor rank
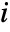 . »
. » - If f and x are both arrays, then D[f,{x}] effectively threads first over each element of f, and then over each element of x. The result is an array with dimensions Join[Dimensions[f],Dimensions[x]]. »
- VectorSymbol, MatrixSymbol or ArraySymbol can be used to indicate that variables or function values are vectors, matrices or arrays.
- D can formally differentiate operators such as integrals and sums, taking into account scoped variables as well as the structure of the particular operator.
- Examples of operator derivatives include:
-
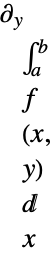
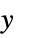 is not scoped by the integral
is not scoped by the integral
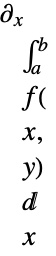
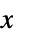 is scoped by the integral
is scoped by the integral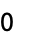
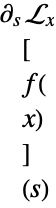
 is not scoped by the integral transform
is not scoped by the integral transform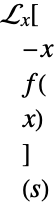
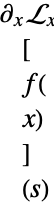
 is scoped by by the integral transform
is scoped by by the integral transform
- All expressions that do not explicitly depend on the variables given are taken to have zero partial derivative.
- The setting NonConstants{u1,…} specifies that ui depends on all variables x, y, etc. and does not have zero partial derivative. »
Examples
open all close allBasic Examples (7)
Scope (89)
Basic Uses (12)
Derivative of an expression with respect to x:
Derivative of an expression at a point:
Derivative of a function at a general point x:
This can also be achieved using fluxion notation:
This can be found more easily using fluxion notation:
The third derivative at the point x==-1:
Derivative involving symbolic functions:
Partial derivatives of an expression with respect to x and y:
The mixed partial derivative ![]() :
:
The mixed partial derivative ![]() :
:
Differentiate with respect to a compound expression:
Differentiate with respect to different compound expressions:
Derivative of a vector expression:
Vector derivative of an expression, also known as the gradient:
Symbolic Functions (9)
Derivative of a symbolic function:
Substitute in a pure function for f to get a particular result:
The chain rule for composite functions:
Product rule for three functions:
State the rule using an Inactive derivative:
Partial derivative of a symbolic function:
Substitute in for f a pure function in two variables:
Derivative of a pure function with respect to non-argument parameters:
The result is the function that at point x gives the derivative of ![]() with respect to a:
with respect to a:
Local variables are independent from the differentiation variable:
Derivative of a symbolic function at a point:
The same, using prime notation:
Derivative of an inverse function:
Elementary Functions (6)
Special Functions (8)
The logarithmic derivative of Gamma is the PolyGamma function:
Derivatives of Airy functions are given in terms of AiryAiPrime and AiryBiPrime:
The derivative of Zeta has a closed-form expression at the origin:
Special functions with elementary derivatives:
Special functions with derivatives expressed in terms of the same functions:
Derivative of JacobiSN:
Derivative of JacobiCD:
Derivative of LogIntegral:
Derivative of ExpIntegralEi:
Derivative of order n for SinIntegral:
Piecewise and Generalized Functions (8)
Derivative of a piecewise function:
Derivative of a ConditionalExpression:
Convert a symbolic function into a piecewise function over the reals to differentiate it:
Compute the piecewise derivative over a finite range:
Classical derivatives of pointwise-defined engineering functions:
Distributional derivatives of generalized functions:
Derivative of RealAbs:
Their counterparts on the complex plane are nowhere differentiable:
Derivative of Floor:
Implicitly Defined Functions (3)
Vector-Valued Functions (5)
The first derivative to a vector-valued function at a general value t:
Computing the same using prime notation:
Computing the same using prime notation:
The derivative of a vector-valued function stored as a SparseArray:
Convert the result to a normal array:
The derivative of matrix represented as a SymmetrizedArray object:
Vector Argument Functions (6)
Gradient of a scalar function:
Jacobian of a vector-valued function:
Second-order derivative tensor:
Compute the derivative of the determinant with respect to the original matrix:
The gradient of a vector-valued function stored as a SparseArray:
The result is another SparseArray, containing only the nonzero entries:
Convert the result to a normal matrix:
Hessian computed as a SparseArray:
The gradient can also be computed as a SparseArray, but in this case it is effectively dense:
Jacobian computed as a SparseArray:
Symbolic Array Arguments and Functions (8)
Derivative of a symbolic vector-valued function with respect to a scalar argument:
Derivative of a symbolic matrix–valued function with respect to a scalar argument:
Derivative of a symbolic array–valued function with respect to a scalar argument:
Derivatives of scalar-valued functions with respect to symbolic vector arguments:
Real symbolic vector argument:
Derivatives of scalar-valued functions with respect to symbolic matrix arguments:
Real symbolic matrix argument:
Derivative of a scalar-valued function with respect to a symbolic array argument:
Derivatives of symbolic array–valued functions with respect to symbolic array arguments:
Integrals and Integral Transforms (6)
Differentiate unevaluated integrals:
Differentiate the Inactive form of an integral to get the fundamental theorem of calculus:
A more general form of the fundamental theorem:
Differentiate an inactive FourierTransform:
Sums and Summation Transforms (4)
Differentiate an unevaluated sum:
Differentiation with respect to the dummy variable gives zero:
Differentiate the Inactive form of a sum:
Differentiate an inactive GeneratingFunction:
Indexed Differentiation (9)
Differentiate with respect to an indexed variable, introducing KroneckerDelta factors:
Use Inactive to prevent expansion of the sum:
Summation indices will be renamed if needed, to avoid name ambiguities:
Differentiate an inactive table with respect to an indexed variable:
Activate the result to get the explicit vector result:
Differentiate an inactive table twice with respect to an indexed variable:
In this case only the j![]() entry is nonzero:
entry is nonzero:
Use any notation for indexed variables in sums and tables:
Differentiate with respect to a symbolic table of indexed variables:
Activating the result gives the explicit gradient:
Differentiate twice with respect to a symbolic table of indexed variables, introducing a dummy index:
Replace symbolic variables with explicit values:
Use symbolic vector differentiation of another symbolic vector:
Vector differentiation of a vector with respect to itself gives the identity matrix:
Functions Defined by Derivatives (5)
Define the derivative with prime notation:
This rule is used to evaluate the derivative:
Define the derivative at a point:
Prescribe values and derivatives of f and g:
Find the derivative of the composition at x=3:
Define a partial derivative with Derivative:
Options (1)
Applications (47)
Geometry of the Derivative (5)
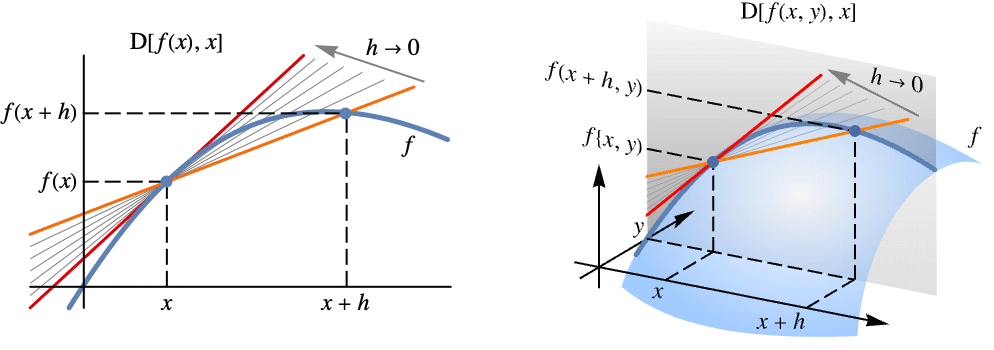
The derivative gives the slope of the tangent line at a point:
For small displacements h from the base point π, the tangent line gives an excellent approximate of f:
The tangent and f are visually indistinguishable from each other over a small, and only a small, plot range:
The derivative gives the limit of the slope of the secant line connecting {x,f[x]} to {x+h,f[x+h]}:
Visualize the process for the point {1,f[1]}:
Find an equation for the tangent line to a function:
General equation for the tangent line at x=a:
Find an equation for the normal line to a function:
General equation for the normal line at x=a:
Find equations for the tangent lines to a function that pass through a point:
Characterization of Functions (5)
Find the turning points on a plane curve:
Find the critical points of a function:
By the second derivative test, these are all maxima or minima:
Visualize the critical points:
Find all values of c that satisfy the Mean Value theorem on an interval:
Define the secant line from a to b:
Define the tangent lines associated with the two values of c:
Visualize the two tangent lines parallel to the secant line along with the original function:
Use the first derivative to characterize a function:
Find the critical points of a function:
Find where the function is increasing:
Find where the function is decreasing:
Use the second derivative to characterize a function:
Find the inflection points of a function:
Find where the function has positive concavity:
Relation to Integration (2)
Multivariate and Vector Calculus (6)
Find the critical points of a function of two variables:
Compute the signs of ![]() and the determinant of the second partial derivatives:
and the determinant of the second partial derivatives:
By the second derivative test, the first two points—red and blue in the plot—are minima and the third—green in the plot—is a saddle point:
Find the curvature of a circular helix with radius r and pitch c:
Obtain the same result using ArcCurvature:
Compute a univariate Taylor series by hand:
Compute a multivariate Taylor series by hand:
Write a function to automate the process:
Recompute the above using the new function:
The gradient vector can be computed by finding the partial derivatives of a function:
Find the gradient vector of the function ![]() :
:
Visualize the direction of the gradient vector using a unit vector representation:
The curl of a vector field on the plane can be computed by subtracting the derivatives of its components:
Find the curl of the vector field ![]() :
:
Visualize the 2D curl as the net "rotation" of the vector field at a point, with red and green representing clockwise and counterclockwise curl, respectively, and radius proportional to the magnitude of rotation:
The divergence of a vector field can be computed by summing the derivatives of its components:
Find the divergence of a 2D vector field:
Visualize 2D divergence as the net "flow" of the vector field at a point, with red and green representing outflow and inflow, respectively, and radius proportional to the magnitude of the flow:
Differential Equations (6)
Construct the differential equation satisfied by an implicit function y[x]:
Use D to specify ordinary and partial differential equations:
These can be solved using DSolve:
Define a wave equation in two spatial variables:
Define initial values for the function and its first time derivative:
Solve the system using DSolve:
Extract a few terms from the Inactive sum:
The two-dimensional wave executes periodic motion in the vertical direction:
Specify a Laplacian operator using D:
Specify homogeneous Dirichlet boundary conditions:
Find the 4 smallest eigenvalues and eigenfunctions of the operator in a unit disk:
Specify an integro-differential equation using D:
Specify an initial condition to obtain a particular solution:
Plot the solutions for different values of a:
Find a second-degree polynomial solution to the differential equation:
Rates of Change (5)
The height of a projectile at time t is given by:
Compute the acceleration at t:
Find when the projectile reaches its maximum height:
Find the maximum height of the projectile:
The area of a circle as a function of time is given by:
Compute the rate of change of area:
Find the rate of change of area at a radius of 10 m if the radius increases at a rate of 5m/s:
The position of a particle is given by:
Compute the velocity, acceleration, jerk, snap (jounce), crackle and pop of the particle:
The total resistance in a circuit of two resistors connected in parallel is given by:
Calculate RT for the given values of R1 and R2:
Find the rate of change of the total resistance:
Calculate the rate of change of the total resistance with the given values:
Volume of a cube in terms of side length l is given by:
Surface area of a cube is given by:
Compute the rate of change of the volume of a cube with respect to surface area using the chain rule:
Solve for l in terms of surface area and substitute that into the result:
Implicit Functions (3)
Optimization (3)
Find the maximum area of a rectangular fence of 2000 ft., bordered on one side by a barn:
Compute the area in terms of width:
By the second derivative test, this value is a true maximum:
Alternately, compute the area in terms of length:
Visualize how the area changes as the length changes:
Find the shortest distance from a curve to the point (1,5):
Compute the distance in terms of y:
By the second derivative test, this is a minimum:
Visualize how the distance changes with position:
Find the dimensions of a lidless, cylindrical can with the least material that can hold up to 2 L of water:
Compute the height in terms of the radius, using the volume constraint:
Compute the surface area in terms of the radius:
The radius corresponding to the minimum surface area:
By the second derivative test, this is a minimum:
Compute the radius, height and surface area of the minimum configuration:
L'Hôpital's Rule (3)
Find the limit of the ratio of two functions as x0:
Directly solving the limit leads to an indeterminate form of type ![]() :
:
L'Hôpital's rule can be used because in an interval around ![]() , both
, both ![]() and
and ![]() are defined, and
are defined, and ![]() :
:
Indeed, ![]() and
and ![]() are continuous, and
are continuous, and ![]() , so
, so ![]() can be computed trivially:
can be computed trivially:
Verify the result using Limit:
Visualize the two functions and their ratio:
Find the limit of the ratio of two functions as x∞:
Directly solving the limit leads to an indeterminate form of type ![]() :
:
L'Hôpital's rule can be used because for all ![]() , both
, both ![]() and
and ![]() are defined, and
are defined, and ![]() :
:
However, using the first derivatives also leads to an indeterminate form:
The second derivatives are constant and obviously satisfy the conditions of L'Hôpital's rule:
Hence ![]() can be computed trivially:
can be computed trivially:
Verify the result using Limit:
Find the limit of the product of two functions as x0:
Directly solving the limit leads to an indeterminate form of type 0×∞:
However, ![]() exists and is positive for all
exists and is positive for all ![]() , and it also exists and is negative for all
, and it also exists and is negative for all ![]() :
:
As ![]() is clearly defined for all real
is clearly defined for all real ![]() , L'Hôpital's rule can be applied in the form:
, L'Hôpital's rule can be applied in the form:
The quotient in the right-hand limit gives a continuous expression whose limit is simple to compute:
Symbolic Array Calculus (6)
Approximate the variance for a perturbed vector:
Since the second derivative does not depend on ![]() , the order two approximation equals the exact value:
, the order two approximation equals the exact value:
Approximate the determinant of a perturbed matrix:
Derive a least-squares solution for data ![]() given as a list of pairs
given as a list of pairs ![]() :
:
Find the vector of vertical deviations ![]() for the data:
for the data:
Define the sum of squares of the vertical deviations for the data:
Set up the least-squares equations:
Solve the least-squares problem for this data:
Find GammaDistribution parameters that best fit the given data using the maximum likelihood method:
Maximize the log-likelihood function ![]() :
:
Find a zero of the gradient, with ![]() replaced by
replaced by ![]() :
:
Compare with the result computed using EstimatedDistribution:
Find an optimality condition for a portfolio optimization problem with the expected return ![]() and standard deviation
and standard deviation ![]() :
:
The goal is to maximize ![]() when the vector
when the vector ![]() of asset weights satisfies Total[x]=1. The constraint can be used to represent
of asset weights satisfies Total[x]=1. The constraint can be used to represent ![]() where the unconstrained vector variable
where the unconstrained vector variable ![]() consists of the first
consists of the first ![]() coordinates of
coordinates of ![]() :
:
The maximum occurs at a critical point of ![]() :
:
Express the condition in terms of ![]() :
:
Compute the gradient of the log-likelihood function of the linear regression model represented by the equation ![]() , where
, where ![]() are normally distributed random variables with mean zero and variance
are normally distributed random variables with mean zero and variance ![]() :
:
The log-likelihood function ![]() is given by:
is given by:
Properties & Relations (23)
The derivative of a function is defined as a limit:
The Limit of DifferenceQuotient is the derivative D:
D is the inverse of Integrate:
The fundamental theorem of calculus:
Differentiation inside of Integrate:
D returns formal results in terms of Derivative:
D differentiates expressions with respect to a given variable:
Derivative is an operator and returns pure-function results:
The derivative of a function at a point may not be available in closed form:
An approximation to the derivative can be obtained using N:
D[f,{array1},…] is essentially equivalent to First[Outer[D,{f},array1,…]]:
If f and a are arrays, Dimensions[D[f,{a}]]==Join[Dimensions[f],Dimensions[a]]:
D[f,{{x1,x2,…,xn}}] is effectively equivalent to Grad[f,{x1,x2,…,xn}]:
Div[{f1,f2,…,fn},{x1,x2,…,xn}] is the trace of the vector derivative of f:
More generally, Div[f,x] is the contraction of the last two dimensions of the vector derivative of f:
Curl[f,x] is ![]() times the HodgeDual of the vector derivative of f, where r is the rank of f:
times the HodgeDual of the vector derivative of f, where r is the rank of f:
For scalar f, Laplacian[f,{x1,x2,…,xn}] is the trace of the second vector derivative of f:
More generally, Laplacian[f,x] is the contraction of the last two dimensions of the second vector derivative of f:
Compute the derivative of Total[a] with respect to a using symbolic arrays:
Compare with the results obtained using indexed differentiation:
ArcCurvature can be defined in terms of D:
Systems of differential equations involving D can be solved with DSolve:
Use D to specify a heat equation with homogeneous Dirichlet boundary conditions:
The eigensystem for this differential system can be found with DEigensystem:
D can be defined using DifferenceDelta:
D can be defined using DiscreteShift:
The right one-sided derivative is computed with a right-hand limit:
The left one-sided derivative is computed with a left-hand limit:
Note that this function is not differentiable at x==0:
D assumes that other variables are independent of the differentiation variable:
Dt assumes that other variables may depend on the differentiation variable:
By manually specifying all other variables as constant, Dt can yield the same result as D:
Compute the derivative of an implicit function using D and Solve:
Use ImplicitD to compute the derivative of an implicit function:
Possible Issues (5)
Results may not immediately be given in the simplest possible form:
Functions given in different forms can yield the same derivatives:
D returns generic results that may not account for discontinuities, cusps or other special points:
Neither f nor g is differentiable at 0:
f is discontinuous, and g has a cusp:
If a function can be expanded into a Piecewise expression, D will provide more accurate results:
Cached values for D may miss changes in underlying definitions:
The issue can be resolved by clearing the system cache:
The variable of differentiation is treated literally:
The following mathematically equivalent input gives 0 because there is no Sin[x] in the first argument:
Interactive Examples (2)
See Also
Dt Derivative DifferenceQuotient Minimize Maximize DSolve NDSolve NDEigensystem NDEigenvalues Integrate Grad Div Curl Laplacian DifferenceDelta CoefficientArrays FractionalD CaputoD ImplicitD
Function Repository: NDerivative FractionalD ListD JacobianMatrix ChainD ProductD FiniteDifferenceStencil
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2004 (5.1) ▪ 2008 (7.0) ▪ 2017 (11.1) ▪ 2024 (14.1)
Text
Wolfram Research (1988), D, Wolfram Language function, https://reference.wolfram.com/language/ref/D.html (updated 2024).
CMS
Wolfram Language. 1988. "D." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/D.html.
APA
Wolfram Language. (1988). D. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/D.html
BibTeX
@misc{reference.wolfram_2025_d, author="Wolfram Research", title="{D}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/D.html}", note=[Accessed: 19-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_d, organization={Wolfram Research}, title={D}, year={2024}, url={https://reference.wolfram.com/language/ref/D.html}, note=[Accessed: 19-January-2026]}