discretizes a 2D or 3D graphic g into a MeshRegion.
DiscretizeGraphics[g,patt]
discretizes only the elements in g that match the pattern patt.




DiscretizeGraphics
discretizes a 2D or 3D graphic g into a MeshRegion.
DiscretizeGraphics[g,patt]
discretizes only the elements in g that match the pattern patt.
Details and Options





- DiscretizeGraphics discretizes graphics into a disjoint union of piecewise linear cells used in MeshRegion.
- The graphic g can be Graphics, Graphics3D, or individual graphics primitives.
- DiscretizeGraphics effectively treats multiple primitives in Graphics and Graphics3D as a union operation.
- The discretization is exact when g contains only bounded piecewise linear primitives; otherwise, it is an approximation.
- Bounded piecewise linear primitives in Graphics (these can be represented exactly):
-
Point[…] point (0D) Line[…] line (1D) Triangle[…] filled triangle (2D) Polygon[…] filled polygon (2D) Rectangle[…] filled rectangle (2D) Parallelogram[…] filled parallelogram (0D, 1D, or 2D) Simplex[…] simplex (0D, 1D, or 2D) - In addition, SSSTriangle, SASTriangle, ASATriangle, and AASTriangle evaluate to Triangle and can be represented exactly.
- Unbounded piecewise linear primitives in Graphics (only a finite range can be represented):
-
HalfLine[…] half-line or ray (1D) InfiniteLine[…] infinite line (1D) HalfPlane[…] half-space (2D) ConicHullRegion[…] linear cone (0D, 1D, or 2D) - Nonlinear primitives in Graphics (only an approximation can be represented):
-
Circle[…] circle, ellipse, sectors (1D) Disk[…] disk, filled ellipse, sectors (2D) BezierCurve[…] Bezier spline curve (1D) BSplineCurve[…] B-spline curve (1D) JoinedCurve[…] joined curve segments (1D) FilledCurve[…] filled closed curve (2D) - In addition, Circumsphere evaluates to Sphere and can be represented approximately.
- Bounded piecewise linear primitives in Graphics3D (these can be represented exactly):
-
Point[…] point (0D) Line[…] line (1D) Triangle[…] filled triangle (2D) Polygon[…] filled polygon (2D) Cuboid[…] filled cuboid (3D) Parallelepiped[…] filled parallelepiped (0D, 1D, 2D, or 3D) Tetrahedron[…] filled tetrahedron (3D) Hexahedron[…] filled hexahedron (3D) Pyramid[…] filled pyramid (3D) Prism[…] filled prism (3D) Simplex[…] simplex (0D, 1D, 2D, or 3D) - Unbounded piecewise linear primitives in Graphics3D (only a finite range can be represented):
-
HalfLine[…] half-line or ray (1D) InfiniteLine[…] infinite line (1D) HalfPlane[…] plane bounded in one direction (2D) InfinitePlane[…] infinite plane (3D) ConicHullRegion[…] linear cone (0D, 1D, 2D, or 3D) - Nonlinear primitives in Graphics3D (only an approximation can be represented):
-
BezierCurve[…] Bezier curve (1D) BSplineCurve[…] B-spline curve (1D) JoinedCurve[…] joined curve segments (1D) BSplineSurface[…] B-spline surface (2D) Sphere[…] sphere (2D) Ball[…] ball or filled sphere (3D) Ellipsoid[…] filled ellipsoid (3D) Cylinder[…] filled cylinder (3D) Cone[…] filled cone (3D) - In addition, Circumsphere evaluates to Sphere and can be represented approximately.
- DiscretizeGraphics has the same options as MeshRegion, with the following additions and changes:
-
AccuracyGoal Automatic digits of accuracy sought MaxCellMeasure Automatic maximum cell measure MeshQualityGoal Automatic quality goal for mesh cells Method Automatic method to use MeshRefinementFunction None function that returns True if a mesh cell needs refinement PlotRange Automatic the range to include PerformanceGoal $PerformanceGoal whether to consider speed or quality PrecisionGoal Automatic digits of precision sought - With AccuracyGoal->a and PrecisionGoal->p, an attempt will be made to keep the maximum distance between the region reg or the discretized region dreg and any point in RegionSymmetricDifference[reg,dreg] to less than
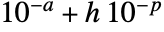 , where
, where 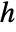 is the length of the diagonal of the plot range.
is the length of the diagonal of the plot range.
Examples
open all close allBasic Examples (3)
Scope (16)
Graphics (9)
Discretize a 2D special region including Circle:
Discretize Graphics with GraphicsComplex containing Point, Line, and Polygon:
Discretize Graphics with GraphicsComplex containing Rectangle, Circle, and Disk:
Discretize only those primitives that match a pattern:
Discretize primitives with dimension less than 2:
Discretize All primitives:
Bounded piecewise linear Graphics primitives can be represented exactly:
Unbounded piecewise linear Graphics primitives can only be represented within a finite range:
Nonlinear Graphics primitives can only be approximately represented:
Graphics involving GraphicsComplex:
Use MaxCellMeasure to control the level of discretization:
Graphics3D (7)
Discretize 3D special regions including Cone:
Discretize Graphics3D with GraphicsComplex containing Point, Line, and Polygon:
Discretize a whole Graphics3D scene, where multiple primitives are taken as a union:
Discretize only those primitives that match a pattern:
Discretize primitives with dimension less than 2:
Discretize All primitives:
Bounded piecewise linear Graphics3D primitives can be represented exactly:
Unbounded Graphics3D primitives can only be represented within a finite range:
Nonlinear Graphics3D primitives can only be approximately represented:
Options (24)
MaxCellMeasure (6)
Discretize with a maximum cell area of 0.1:
This gives the area of the cells:
Discretize with a maximum cell volume of 0.1:
A Histogram of the cell volumes:
Compare different length settings:
Compare different area settings:
MeshCellHighlight (2)
MeshCellHighlight allows you to specify highlighting for parts of a MeshRegion:
MeshCellLabel (3)
MeshCellLabel can be used to label parts of a MeshRegion:
Label the vertices and edges of a parallelogram:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a MeshRegion:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction allows you to specify functions for parts of a MeshRegion:
MeshCellStyle (2)
MeshCellStyle allows you to specify styling for parts of a MeshRegion:
PlotRange (4)
PrecisionGoal (1)
Compare the results for each setting of PrecisionGoal:
Applications (4)
Compute the length of a curve by converting it to a geometric region:
Compute the surface area of a graphic by converting it to a geometric region:
Convert Text to a geometric region:
Properties & Relations (9)
Multiple primitives are interpreted as a union:
Bounded linear primitives can be exactly discretized:
Unbounded linear primitives can only be represented within a finite range:
Nonlinear primitives can only be approximately discretized:
Use BoundaryDiscretizeGraphics to get a BoundaryMeshRegion representation:
DiscretizeRegion can be used to discretize any RegionQ object:
DiscretizeGraphics can be used to discretize Graphics and Graphics3D objects:
They can both discretize special regions that are also graphics primitives:
Graphics primitives that are also geometric regions can be used without discretization:
Compute directly with the region:
Or with its discretized version:
Rasterize discretizes any rendered expression to Graphics containing a Raster object:
Image discretizes any rendered expression to an Image object:
See Also
BoundaryDiscretizeGraphics DiscretizeRegion MeshRegion BoundaryDiscretizeRegion FindMeshDefects RepairMesh RegionImage
Function Repository: GraphicsMetricGraph
Related Guides
Text
Wolfram Research (2014), DiscretizeGraphics, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscretizeGraphics.html (updated 2015).
CMS
Wolfram Language. 2014. "DiscretizeGraphics." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DiscretizeGraphics.html.
APA
Wolfram Language. (2014). DiscretizeGraphics. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscretizeGraphics.html
BibTeX
@misc{reference.wolfram_2025_discretizegraphics, author="Wolfram Research", title="{DiscretizeGraphics}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DiscretizeGraphics.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretizegraphics, organization={Wolfram Research}, title={DiscretizeGraphics}, year={2015}, url={https://reference.wolfram.com/language/ref/DiscretizeGraphics.html}, note=[Accessed: 09-January-2026]}