CellularAutomaton

CellularAutomaton[rule,init,t]

产生一个表示元胞自动机演化的列表，该元胞自动机指定的规则，其初始条件 init，共有 t 步.

CellularAutomaton[rule,init]

给出 init 演化一步的结果.

CellularAutomaton[rule,init,{tspec,xspec,…}]

仅给出由 tspec、xspec，等指定的演化部分.

CellularAutomaton[rule,init,{t,All,…}]

i在各步包括在 t 步中受影响的所有元胞.

CellularAutomaton[rule]

是 CellularAutomaton 的操作符形式，表示演化过程中的一步.

更多信息

  • rule 的可能形式有：
  • n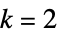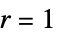，，规则号为 n 的初等规则
    {n,k}产生 k 色的最近邻规则
    {n,k,r}产生 k 色、范围为 r 的一般规则
    {n,k,{r1,r2,…,rd}}按 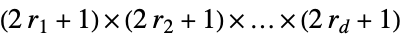邻近的 d 维规则
    {n,k,{{off1},{off2},…,{offs}}} 指定偏移量的近邻规则
    {n,k,rspec,s}s 阶规则
    {n,{k,1}}k 色最近邻极权规则
    {n,{k,1},r}k 色、范围为 r 的极权规则
    {n,{k,{wt1,wt2,…}},rspec}近邻 i 的权重被赋为 wti 的规则
    {lhs1->rhs1,lhs2->rhs2,…}近邻列表的明确替换
    {fun,{},rspec}应用于各个近邻列表的一般函数 fun
    bfun应用于近邻集合的布尔函数
    CellularAutomaton[rule]规则的运算符形式
    <|"key1"val1,"key2"val2,…|>由关联给出的规范
    "name"已命名规则
  • CellularAutomaton[{n,k},…] 等价于 CellularAutomaton[{n,{k,{k^2,k,1}}},…].
  • 可以使用下面的键来指定以关联形式给出的规则：
  • "RuleNumber"n规则编号
    "TotalisticCode"n极权代码
    "OuterTotalisticCode"n外部极权代码
    "GrowthCases"{g1,g2,…}当其邻域的 gi 为 1 时把元胞置 1
    "GrowthSurvivalCases"{{g1,…},{s1,…}}把 gi 邻域置 1；保持 si 不变
    "GrowthDecayCases"{{g1,…},{d1,…}}把 gi 邻域置 1；di 置 0
    "Dimension"d整体维度
    "Colors"k颜色的数量
    "Range"r规则范围
    "Neighborhood"type邻域类型
  • 当设置为 "GrowthCases"->{g1,g2,…} 时，如果一个元胞有 gi 个邻域为 1 时，它的值从 0 变为 1；否则它的值不变.
  • 当设置为 "GrowthSurvivalCases"->{{g1,…},{s1,…}} 时，如果一个元胞有 gi 个邻域为 1 时，它的值从 0 变为 1，如果有 si 个邻域为 1 时，保持值为 1，否则值为 0.
  • 当设置为 "GrowthDecayCases"->{{g1,…},{d1,…}} 时，如果一个元胞有 gi 个邻域为 1 时，它的值从 0 变为 1，如果有 di 个邻域为 1 时，值为 0 ，否则保持不变.
  • 二维 "Neighborhood" 的可能设置包括：
  • 5 或 "VonNeumann"CrossMatrix[1]
    9 或 "Moore"BoxMatrix[1]
  • 对于维度 d，"Neighborhood" 支持 "VonNeumann" 和 "Moore"，以及整数 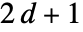和 .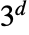
  • 以 CellularAutomaton["name",…] 形式给出的可能的已命名的元胞自动机规则包括：
  • "Rule30"30
    "Rule90"90
    "Rule110"110
    "Code1599"{1599,{3,1}}
    "GameOfLife"{224,{2,{{2,2,2},{2,1,2},{2,2,2}}},{1,1}}
  • 常见的二维元胞自动机规则的明确形式包括：
  • {n,{k,1},{1,1}}9 近邻极权规则
    {n,{k,{{0,1,0},{1,1,1},{0,1,0}}},{1,1}}
    5 近邻极权规则
    {n,{k,{{0,k,0},{k,1,k},{0,k,0}}},{1,1}}
    5 近邻外部极权规则
  • 元胞自动机规则的可能数量如下：
  • 基本规则256
    一维常规规则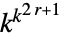
    一维极权规则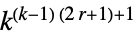
    二维常规规则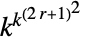
    二维9近邻极权规则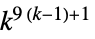
    二维5近邻极权规则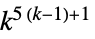
    二维5近邻外部极权规则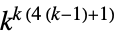
  • 通常，init 中的所有元素在和演化列表是 0 和 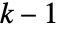间的整数.
  • 当使用一般函数或替换列表时， init 的元素和演化列表可以是任何表达式. »
  • 明确替换规则 lhsi->rhsi 可以包括模式.
  • 在一维元胞自动机中，替换规则或明确函数 fun 可以用于一维近邻列表. 若近邻指定明确偏移量，则它们按偏移量顺序给定.
  • 当多维元胞自动机的近邻在指定范围内定义，例如 {r1,r2,…}，则近邻列表采用 2{r1,r2,…}+1 维全数组.
  • 若多维元胞自动机的近邻由显式偏移量列表指定，则近邻按指定顺序的偏移量的一维列表提供.
  • 若给定明确函数 fun，则所提供的第一个自变量将是近邻列表，第二自变量是从 0 开始的步数.
  • 如果 BooleanVariables[bfun] 产生一个整数 v，则完整的规则说明被认为是纯布尔函数 bfun. 在这种情况下，bfun 将在每一步应用于 v 元胞的近邻. 这个近邻将把 Ceiling[v/2] 个元胞扩展到左侧.
  • 在由 {rule,kspec,rspec,s} 指定的 s 阶元胞自动机中，各步取决于之前的 s 步.
  • 初始情况由 init 构造如下：
  • {a1,a2,…}假定循环时，值 ai 的明确列表
    {{a1,a2,…},b}值 ai 叠加于背景 b 上
    {{a1,a2,…},{b1,b2,…}}值 ai 叠加于重复背景 b1、b2、…
    {{{{a11,a12,…},off1}, {{a21,…},off2},…},bspec}
    值 aij 在背景的偏移量 offi
    {{a11,a12,…},{a21,…},…}二维明确值列表
    {aspec,bspec}d 维填充下的 d 维值
  • aspec 的第一个元素被叠加的背景位于各个坐标正向相对原点的第一个坐标处. 也就是说，bspec[[1,1,…]] 与 aspec[[1,1,…]] 对齐.
  • CellularAutomaton[rule,init,t] 生成长度为 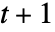的演化列表.
  • 对 s 阶元胞自动机，init 是给出演化系统中初始 s 步的一个列表.
  • {tspec,xspec,…} 中的时间指定 tspec 如下：
  • t0 到 t 的所有步
    {t}仅包含第 t 步的列表
    {{t}}仅第 t 步
    {t1,t2}第 t1 到 t2 步
    {t1,t2,dt}步 t1, t1+dt, …
  • 第 0 步作为初始条件.
  • CellularAutomaton[rule,init,{tspec}] 的 xspec 使用缺省 Automatic.
  • 空间指定 xspec 如下：
  • All受指定的初始情况影响的所有元胞
    Automatic与背景不同的区域内的所有元胞
    0与 aspec 的开始对齐的元胞
    x向右的偏移量至多为 x 的元胞
    -x向左的偏移量至多为 x 的元胞
    {x}向右的偏移量为 x 的元胞
    {-x}向左的偏移量为 x 的元胞
    {x1,x2}偏移量为 x1 到 x2 的元胞
    {x1,x2,dx}元胞 x1, x1+dx, …
  • 一维时，aspec 的第一个元素在缺省的情况下有空间偏移量 0.
  • 在任意维数时，aspec[[1,1,1,…]] 在缺省的情况下有空间偏移量 {0,0,0,…}.
  • 由 CellularAutomaton 生成的演化列表的各个元素恒有相同的大小.
  • 在由宽度为 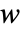的 aspec 指定的初始条件下，在 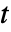步后能够被范围为 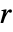的规则影响的的区域具有宽度 .
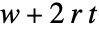  • 若 bspec 背景不被指定，则 All 和 Automatic 的空间偏移量将包括 aspec 的每个元胞.
  • All 的空间偏移量包括初始条件下所有受影响的元胞.
  • Automatic 的空间偏移量可用于剪切元胞自动机模式各边的背景.
  • 在确定区域的宽度时，Automatic 仅考虑由 offt 指定的各步的结果.
  • CellularAutomaton[rule][init] 等价于 CellularAutomaton[rule,init].

范例

打开所有单元关闭所有单元

基本范例  (3)

运行规则 30 两步：

在 0 的背景上从1 运行 50 步：

生成元胞自动机规则的符号：

范围  (91)

一维规则  (26)

基本规则 73：

用 RulePlot 产生同样的结果：

三色规则 679458：

生成规则图标：

代码为 867 的三色极权规则：

范围是 的两色规则（左边两个近邻，右边一个近邻）：

普通范围 的规则：

代码为10的 极权规则：

元胞的近邻有明确偏移量的规则 30：

修正偏移量的模拟规则 30：

具有 2 个近邻的规则：

元胞的近邻有明确权重的规则 30：

三色极权规则：

极权规则的近邻各个偏移量重 1：

三色外部极权规则：

通过给出近邻的明确替换指定规则 90：

通过给出一个单一“代数”替换规则指定规则 90 ：

对规则 30 使用明确布尔公式，在 True 和 False 状态下操作：

元胞自动机的值可以是任何符号表达式：

使用任意符号函数 f 作为规则应用于范围为 1 的近邻：

将该函数应用于偏移量是 和 的近邻：

设置一个“帕斯卡三角元胞自动机”：

指定规则 90 作为明确函数：

叠加性元胞自动机模除 4：

函数的的第二自变量给定步数：

在连续步骤上改变规则；#2 给出步数：

使用元胞的连续值：

指定规则 90 为纯布尔函数：

使用纯布尔函数, 一个 规则 90 的模拟：

用关联指定的规则  (5)

用关联指定规则 30：

三色元胞自动机：

2 色、范围为 3/2 的元胞自动机：

三色极权元胞自动机：

三色外部极权元胞自动机：

初始条件  (8)

明确初始条件认为是循环的：

最左元胞的左近邻是最右元胞，反之亦然：

随机初始条件：

由“种子”开始，该种子包括由 0 环绕的 11101 块：

从由 1 环绕的唯一 0 开始：

从背景为10个重复块的111开始：

指定“种子”作为一个稀疏数组：

使用 SparseArray 给出完全的循环初始条件：

从偏移量为 的块101和偏移量为 的块 开始：

时间步  (6)

演化两步：

其它形式：

仅包括第二步的列表：

第二步，不在列表里：

步骤 50 至 80：

初始条件是第 0 步：

显示从 0 到 100 的各个第三步：

区域规范  (11)

缺省的情况下，CellularAutomaton 自动切除不被模式覆盖的区域：

一个等效形式：

包括受规则结构影响的所有元胞：

包括仅区别于背景的区域：

包括可能受影响的所有区域的元胞：

缺省的情况下，不同规则给出不同宽度的区域：

强制同类型的所有规则给出相同宽度的区域：

受影响的区域取决于规则的范围：

仅显示从元胞 0（初始 1 的位置）到元胞 40 的区域：

负数位置在左边：

给出仅由各步的元胞 0 组成的区域：

仅包括元胞 0 的值，而不是列表：

显示时间和空间上的每隔一个元胞：

元胞 0 恒为初始条件明确部分的最左边的元胞：

重复一个有限块，填充位置从 到 的初始条件下的区域：

多维规则  (13)

演化范围为1的二维（9近邻）极权码14两步：

仅给出两步后的结果：

显示 30 步后的结果：

显示各个元胞的平均色：

用三维图像显示空间-时间演变历史：

在各个 1 元胞位置显示立方体：

空间时间的 50 步切片将在 偏移量为 0 处横跨所有 的值：

所有元胞在 位置的平均色：

用 RulePlot 可视化极权规则规范：

5 近邻极权规则：

5 近邻外部极权规则：

用 RulePlot 可视化外部极权规则规范：

指定在稀疏数组中用两个黑元胞作为初始条件：

三维最近邻极权元胞自动机：

用关联指定的多维规则  (8)

用关联（假定有 9 个邻域）指定二维极权代码 14：

5 邻域极权代码 26：

用字符串 "VonNeumann" 描述邻域：

5 邻域外部极权代码 110：

（9 个邻域中）当元胞有 1 个或 2 个邻域的值为 1 时的生长规则：

三维图像：

当元胞有 1 个或 2 个邻域的值为 1 时，元胞的值为 1，当元胞有 6 个或 7 个邻域的值为 1 时，元胞的值为 0 的生长衰灭规则：

当元胞有 1 个或 2 个邻域的值为 1 时，元胞的值为 1，当元胞有 6 个或 7 个邻域的值为 1 时，元胞的值保持不变，否则值为 0 的规则：

（7 个邻域中）当元胞有 1 个邻域的值为 1 时，元胞的值为 1：

（27 个邻域中）当元胞有 1 个邻域的值为 1 时，元胞的值为 1：

高阶规则  (6)

规则 30 被明确写为“一阶规则”：

规则 30 的二阶模拟包括两步初始条件：

在输出中包括两个初始条件：

二阶规则 1008，在两个初始条件步均以 1 开始：

包括两个初始条件步：

2色、范围1的二阶极权规10：

同一规则的 12 阶版本：

规则 150R——二阶可逆模除 2 规则：

二阶极权算在 2 色和范围 1 下的空间时间部分：

同一规则的第 50 步：

函数版本  (6)

给出规则 30 演化一步的结果：

另一种形式：

单步迭代三次：

给出 3 步的演化结果：

给出由重复背景围绕的中心区域的结果：

规则 45 给出一步之后的由1组成的背景：

迭代单步规则 45：

以操作形式指定规则：

由字符串指定的特殊规则  (2)

用字符串指定规则 30：

用字符串指定生命游戏 (Game of Life) 的规则:

应用  (23)

制作一张规则 30 的彩色图片：

制作前32个基本元胞自动机的图片：

从一系列初始条件中显示 2 色、范围为 2 的极权码为 20 的元胞自动机，

显示 3 色、范围为 3 的极权码 1599 的不同初始条件的结果：

各个模式的边上用三个 0 填充：

显示多”面板“的一个单一演化：

显示规则 30 的 200 步：

用规则 30 的中心列在元胞值处”随意“行走：

找出规则 90 在连续宽度的循环区域重复期：

绘制规则 110 在大小为 7 时的区域处的状态转换图：

为初始条件相差一个比特的两个元胞自动机生成一个差异模式：

用灰色显示一般演化：

使用外极权二维元胞自动机生成迷宫状图案：

用生长规则产生不规则图案：

显示 5 近邻外极权二维元胞自动机的演化步骤：

在“生命游戏”中显示“滑块”：

在“生命游戏”中显示“呼啸的火车”的演化：

“生命游戏”初始条件随意，平均 100 步：

平均空间时间片断：

由一系列二维 9 近邻法则产生的模式：

平均元胞值：

使用球体渲染一个二维元胞自动机的演化的三维视图：

显示三维元胞自动机演化的一系列步骤：

在三维元胞自动机中显示一系列高度的时间平均片断：

构建帕斯卡三角：

基于复杂整数乘法的元胞自动机：

代数简化的模数为 3 的叠加性规则：

属性和关系  (9)

包括网格线：

为元胞加标签：

突出元胞中心列：

用 RulePlot 生成图形：

用 Image 生成图像，其中每个元胞是一个像素：

步自动元胞机演化给出长度为 的列表：

初始条件下给定的明确列表假定是循环的：

中心元胞从所有可能的元组开始，给出规则数的位数：

这里是 5 邻域外部极权代码：

生成它的 RulePlot：

与之等同的生长-存活形式的规则：

生长-衰灭形式的规则：

可能存在的问题  (7)

缺省的情况下，各个演化列表只取必要的长度：

使用 {t,All} 使一个特定类型的所有法则具有相同长度的列表：

若没有元胞和背景不同，在自动选择区域将总为空：

交替背景法则可给出只包含 0 的列表：

若演化为连续两步，则在一步的结果内包括显式的1：

在这种形式下，包括背景的一种指定：

缺省的情况下，各个演化只取必要的宽度：

使用 {t,All} 得到一致宽度：

三色规则可能只给出值 0 和 1：

如果用 ArrayPlot 来可视化，值 1 将被显示为黑色：

用 RulePlot 基于相应的值显示正确的颜色：

显式 ColorRules 也可以避免 ArrayPlot 的默认设置造成的问题：

用 RulePlot 来显示相应的值：

在 CellularAutomaton 中元胞和步骤不根据它们的部分号码编号：

当偏移量用不同的次序指定时，规则号具有不同的意义：

Wolfram Research (2002)，CellularAutomaton，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CellularAutomaton.html （更新于 2017 年）.

文本

Wolfram Research (2002)，CellularAutomaton，Wolfram 语言函数，https://reference.wolfram.com/language/ref/CellularAutomaton.html （更新于 2017 年）.

CMS

Wolfram 语言. 2002. "CellularAutomaton." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/CellularAutomaton.html.

APA

Wolfram 语言. (2002). CellularAutomaton. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CellularAutomaton.html 年

BibTeX

@misc{reference.wolfram_2024_cellularautomaton, author="Wolfram Research", title="{CellularAutomaton}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/CellularAutomaton.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cellularautomaton, organization={Wolfram Research}, title={CellularAutomaton}, year={2017}, url={https://reference.wolfram.com/language/ref/CellularAutomaton.html}, note=[Accessed: 17-November-2024 ]}