CentralMoment

CentralMoment[data,r]

data の r 次中心モーメント を与える．

CentralMoment[data,{r1,…,rm}]

data の次数が{r1,…,rm}の多変量中心モーメント を与える．

CentralMoment[dist,…]

分布 dist の中心モーメントを与える．

CentralMoment[r]

r 次の形式的な中心モーメントを表す．

詳細

  • CentralMomentは平均まわりのモーメントとしても知られている．
  • 次数 r のスカラー，data は配列 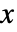，平均（最初の生のモーメント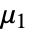）では以下のようになる．
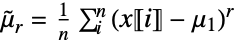
  • x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]r 次ベキの和 »
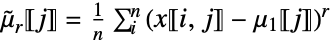
    x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]列ごとの r 次中心ベキの和 »
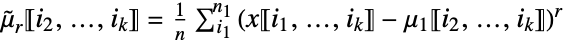
    x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]列ごとの r 次中心ベキの和 »
  • CentralMoment[x,r]はArrayReduce[CentralMoment[#,r]&,x,1]に等しい．
  • 次数{r1,…,rm}のベクトル， data は配列 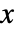，最初の生のモーメント 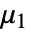では以下のようになる．
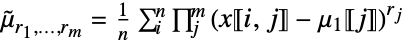
  • x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]第 j 列の rj次中心ベキの和
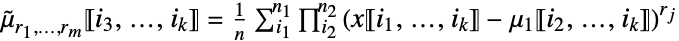
    x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]第 j 列の rj次中心ベキの和　 »
  • CentralMoment[x,{r1,…,rm}]はArrayReduce[CentralMoment[#,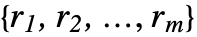{r_1,r_2,...,r_m}]&,x,{{1},{2}}]に等しい．
  • CentralMomentは数値データと記号データの両方を扱うことができる．
  • data は，次の追加的な形式と解釈を持つことができる．
  • Association値（キーは無視される） »
    WeightedDataもとになっているEmpiricalDistributionに基づいた加重平均 »
    EventDataもとになっているSurvivalDistributionに基づく »
    TimeSeries, TemporalData, …値のベクトルまたは配列（タイムスタンプは無視される） »
    Image,Image3DRGBチャンネルの値またはグレースケールの強度値 »
    Audioすべてのチャンネルの振幅値 »
    DateObject, TimeObject日付のリストまたは時間のリスト »
  • 分布 dist について，r 次中心モーメントはExpectation[(x-Mean[dist])r,xdist]で与えられる． »
  • 多変量分布 dist について，{r1,…,rm}次中心モーメントはExpectation[(x1-μ1)r1⋯(x2-μm)rm,{x1,…,xm}dist]および{μ1,…,μm}=Mean[dist]で与えられる． »
  • ランダム過程 proc については，中心モーメント関数は時点 t におけるスライス分布SliceDistribution[proc,t]について 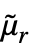mu^~_r[t]=CentralMoment[SliceDistribution[proc,t],r]として計算することができる． »
  • CentralMoment[r]は，MomentConvert，MomentEvaluate等の関数とともに使うことができる． »

例題

すべて開くすべて閉じる

例  (3)

データから中心モーメントを計算する：

記号データを使う：

日付のリストの中心モーメント：

一変量分布の二次中心モーメントを計算する：

多変量分布の中心モーメント ：

スコープ  (26)

基本的な用法  (6)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

WeightedDataの中心モーメントを求める：

EventDataの中心モーメントを求める：

TimeSeriesの中心モーメントを求める：

中心モーメントは値のみに依存する：

数量を含むデータについての中心モーメントを求める：

配列データ  (5)

行列についてのCentralMomentは列ごとのモーメントを返す：

配列についてのCentralMomentは第1レベルの列ごとのモーメントを返す：

配列についての多変量CentralMoment：

大きい配列に使うことができる：

入力がAssociationのとき，CentralMomentはその値に作用する：

SparseArrayデータは密な配列のように使うことができる：

QuantityArrayの中心モーメントを求める：

画像データと音声データ  (2)

RGB画像のチャンネルごとの中心モーメント：

グレースケール画像の中心モーメント強度値：

CentralMomentは，音声オブジェクトについてはチャンネルごとに作用する：

日付と時間  (4)

日付の中心モーメントを計算する：

日付の重み付き中心モーメントを計算する：

異なる暦で与えられた日付の中心モーメントを計算する：

分散と比較する：

時間の中心モーメントを計算する：

異なる時刻帯指定の時刻のリスト：

分布のモーメントと過程のモーメント  (5)

一変量分布のスカラー中心モーメント：

多変量分布のスカラー中心モーメント：

多変量分布の結合中心モーメント：

記号次数 r についての中心モーメントを計算する：

中心モーメントは特定の次数についてしか評価できないことがある：

中心モーメントは数値的にしか評価できないことがある：

派生分布についての中心モーメント：

データ分布について：

ランダム過程についての中心モーメント関数：

ある時点 t=0.5におけるTemporalDataの中心モーメントを求める：

対応する中心モーメント関数をすべてのシミュレーションとともに求める：

形式的なモーメント  (4)

形式的なモーメントのTraditionalFormによる表示：

形式的なモーメントの組合せをCentralMomentを含む式に変換する：

形式的なモーメントを含む式 TemplateBox[{2}, CentralMoment]+TemplateBox[{4}, CentralMoment] を分布について評価する：

データについて評価する：

CentralMomentを含む式のサンプル推定量を求める：

結果の推定量をデータについて評価する：

アプリケーション  (11)

一次中心モーメントは常に0である：

二次中心モーメントは分散度である：

三次中心モーメントは歪度の尺度である：

モーメント法を使って分布母数を推定する：

データと推定されたパラメトリック分布を比較する：

モーメント法を使ってGammaDistributionの正規近似を求める：

と が と にいかに依存しているかを示す：

もとの分布と近似された分布を比較する：

二次中心モーメントのサンプル推定器を構築する：

サンプルサイズが であると仮定してサンプル分布の期待値を求める：

推定器のサンプル分布分散を求める：

一様分布に従うサンプルの推定器の分散：

大数の法則にはサンプルサイズが増大するにつれてサンプルモーメントが母集団のモーメントに近付くとある．Histogramを使ってさまざまなサンプルサイズについて一様分布に従う確率変量のサンプルの二次中心モーメントの確率分布を示す：

三次および四次中心モーメントを訂正するほぼ正規分布に従うデータのエッジワース(Edgeworth)展開 ：

Jarque–Bera統計サンプルを計算する関数 [リンク]：

正規分布に従う確率変量のサンプルについての累積統計：

統計ヒストグラムを漸近分布と比較する：

あるデータの移動中心モーメントを計算する：

長さ.1の窓を使う：

ランダム過程の経路集合のスライスについて，中心モーメントを計算する：

いくつかの時間のスライスを選ぶ：

これらの経路についての中心モーメントをプロットする：

特性と関係  (11)

中心モーメントは並進不変である：

二次中心モーメントはスケールされたVarianceである：

2×2行列の奇数のモーメントは消滅する：

多変量次数については，次数の合計が奇数でなければならない：

深さ の配列の多変量中心モーメントの深さは である：

二次中心モーメントのSqrtはMeanからの偏差のRootMeanSquareである：

Skewnessは三次中心モーメントと二次中心モーメントのベキの比である：

Kurtosisは四次中心モーメントと二次中心モーメントのベキの比である：

CentralMomentはそれ自身の平均周辺にある確率変数のベキのExpectationに等しい：

次数 のCentralMomentとが存在する場合，両者は等しい：

CentralMomentを直接使う：

GeneratingFunctionを使って中心モーメント母関数を求める：

CentralMomentGeneratingFunctionの直接評価と比較する：

CentralMomentはMoment，Cumulant，FactorialMoment等によって表すことができる：

考えられる問題  (2)

高次数の中心モーメントは裾部が重い分布については定義されない：

5つの独立した分布サンプルの中心モーメントを計算する：

高次数のサンプル中心モーメントは乱高下を示す：

中心モーメントのサンプル推定器は偏っている：

サイズ のサンプルを仮定してサンプリング母集団の期待値を求める：

推定器は漸近的に不偏である：

不偏推定器を構築する：

推定器の期待値はすべてのサンプルサイズの中心モーメントである：

おもしろい例題  (1)

20個，100個，300個のサンプルについてのCentralMoment推定値の分布：

Wolfram Research (2007), CentralMoment, Wolfram言語関数， https://reference.wolfram.com/language/ref/CentralMoment.html （2024年に更新）.

テキスト

Wolfram Research (2007), CentralMoment, Wolfram言語関数， https://reference.wolfram.com/language/ref/CentralMoment.html （2024年に更新）.

CMS

Wolfram Language. 2007. "CentralMoment." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/CentralMoment.html.

APA

Wolfram Language. (2007). CentralMoment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CentralMoment.html

BibTeX

@misc{reference.wolfram_2024_centralmoment, author="Wolfram Research", title="{CentralMoment}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CentralMoment.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_centralmoment, organization={Wolfram Research}, title={CentralMoment}, year={2024}, url={https://reference.wolfram.com/language/ref/CentralMoment.html}, note=[Accessed: 14-November-2024 ]}