CentralMoment[data,r]
给出 data 的 r![]() 阶中心矩
阶中心矩 ![]() .
.
CentralMoment[data,{r1,…,rm}]
给出 data 的 {r1,…,rm} 阶多变量中心矩 ![]() .
.
CentralMoment[dist,…]
给出分布 dist 的中心矩.
代表正式 r![]() 阶中心矩.
阶中心矩.


CentralMoment
CentralMoment[data,r]
给出 data 的 r![]() 阶中心矩
阶中心矩 ![]() .
.
CentralMoment[data,{r1,…,rm}]
给出 data 的 {r1,…,rm} 阶多变量中心矩 ![]() .
.
CentralMoment[dist,…]
给出分布 dist 的中心矩.
代表正式 r![]() 阶中心矩.
阶中心矩.
更多信息


- CentralMoment 也称为关于均值的矩.
- 对于标量阶 r 且 data 为数组
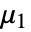 ,平均值(第一原始矩)为
,平均值(第一原始矩)为  :
: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/CentralMoment.zh/8.png)

r  次幂之和 »
次幂之和 »![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/CentralMoment.zh/11.png)

r  次中心幂之纵向和 »
次中心幂之纵向和 »![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/CentralMoment.zh/14.png)

r 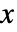 次中心幂之纵向和 »
次中心幂之纵向和 » - CentralMoment[x,r] 等价于 ArrayReduce[CentralMoment[#,r]&,x,1].
- 对于向量阶 {r1,…,rm} 且 data 为数组
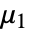 ,第一原始矩为
,第一原始矩为  :
: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/CentralMoment.zh/19.png)

第 j 列的 rj  次中心幂之和
次中心幂之和![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/CentralMoment.zh/22.png)

第 j 列的 rj 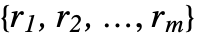 次中心幂之和 »
次中心幂之和 » - CentralMoment[x,{r1,…,rm}] 等价于 ArrayReduce[CentralMoment[#,
 ]&,x,{{1},{2}}].
]&,x,{{1},{2}}]. - CentralMoment 能够处理数值型和符号型数据.
- data 还可以有以下形式和解释:
-
Association 值(忽略键值) » WeightedData 加权平均值,基于底层 EmpiricalDistribution » EventData 基于底层 SurvivalDistribution » TimeSeries, TemporalData, … 值的向量或数组(时间戳忽略不计) » Image,Image3D RGB 通道值或灰度强度值 » Audio 所有通道的振幅值 » DateObject, TimeObject 日期列表或时间列表 » - 对于分布 dist,r
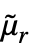 阶中心矩由 Expectation[(x-Mean[dist])r,x∈dist] 给出. »
阶中心矩由 Expectation[(x-Mean[dist])r,x∈dist] 给出. » - 对于多元分布 dist,{r1,…,rm} 阶中心矩由 Expectation[(x1-μ1)r1⋯(x2-μm)rm,{x1,…,xm}dist] 和 {μ1,…,μm}=Mean[dist] 给出. »
- 对于随机过程 proc,可以计算出时间 t 的切片分布的中心矩函数 SliceDistribution[proc,t],因为
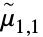 [t]=CentralMoment[SliceDistribution[proc,t],r]. »
[t]=CentralMoment[SliceDistribution[proc,t],r]. » - CentralMoment[r] 可用于诸如 MomentConvert 和 MomentEvaluate 等函数中.
范例
打开所有单元 关闭所有单元范围 (26)
基础用法 (6)
数组数据 (5)
矩阵的 CentralMoment 按列给出矩:
张量的 CentralMoment 在第一层按列给出矩:
数组的多变量 CentralMoment:
当输入是 Association 时,CentralMoment 会对其值进行处理:
SparseArray 数据可以像密集数组一样使用:
求 QuantityArray 的中心矩:
图像和音频数据 (2)
分布与过程矩 (5)
求 TemporalData 在某时刻 t=0.5 的中心矩:
正式矩 (4)
应用 (11)
使用矩方法,求 GammaDistribution 的正态近似:
根据大数定理,随样本量增大,样本矩趋近于总体矩. 使用 Histogram 说明在不同样本量时,一个均匀随机变量的二阶样本中心矩的概率分布:
计算样本 Jarque–Bera 统计量的函数 [链接]:
属性和关系 (11)
二阶中心距是一个缩放后的 Variance:
二阶中心距的 Sqrt 是来自 Mean 的偏差的 RootMeanSquare:
Skewness 是三阶中心距和二阶中心距的乘方的比:
Kurtosis 是四阶中心距和二阶中心距的乘方的比:
CentralMoment 等价于一个随机变量在均值附近的幂的 Expectation:
阶数为 ![]() 的 CentralMoment 等价于
的 CentralMoment 等价于 ![]() ,当两者都存在的情况下:
,当两者都存在的情况下:
直接使用 CentralMoment:
利用 GeneratingFunction 求中心矩母函数:
与 CentralMomentGeneratingFunction 的直接计算比较:
CentralMoment 可以使用 Moment、Cumulant 或者 FactorialMoment 表示:
可能存在的问题 (2)
巧妙范例 (1)
对 20、100和 300 个样本 CentralMoment 的分布估计:
技术笔记
-
▪
- 描述统计
相关指南
-
▪
- 统计矩与母函数 ▪
- 日期和时间 ▪
- 描述性统计分析 ▪
- 符号向量、矩阵和数组
相关的工作流程
- 分析可计算的数据集
文本
Wolfram Research (2007),CentralMoment,Wolfram 语言函数,https://reference.wolfram.com/language/ref/CentralMoment.html (更新于 2024 年).
CMS
Wolfram 语言. 2007. "CentralMoment." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/CentralMoment.html.
APA
Wolfram 语言. (2007). CentralMoment. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/CentralMoment.html 年
BibTeX
@misc{reference.wolfram_2025_centralmoment, author="Wolfram Research", title="{CentralMoment}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/CentralMoment.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_centralmoment, organization={Wolfram Research}, title={CentralMoment}, year={2024}, url={https://reference.wolfram.com/language/ref/CentralMoment.html}, note=[Accessed: 06-February-2026]}