--- title: "ComplexStreamPlot" language: "en" type: "Symbol" summary: "ComplexStreamPlot[f, {z, zmin, zmax}] generates a streamline plot of the vector field {Re[f], Im[f]} over the complex rectangle with corners zmin and zmax." canonical_url: "https://reference.wolfram.com/language/ref/ComplexStreamPlot.html" source: "Wolfram Language Documentation" related_guides: - title: "Complex Visualization" link: "https://reference.wolfram.com/language/guide/ComplexVisualization.en.md" - title: "Vector Visualization" link: "https://reference.wolfram.com/language/guide/VectorVisualization.en.md" related_functions: - title: "ComplexVectorPlot" link: "https://reference.wolfram.com/language/ref/ComplexVectorPlot.en.md" - title: "StreamPlot" link: "https://reference.wolfram.com/language/ref/StreamPlot.en.md" - title: "VectorPlot" link: "https://reference.wolfram.com/language/ref/VectorPlot.en.md" - title: "ListStreamPlot" link: "https://reference.wolfram.com/language/ref/ListStreamPlot.en.md" - title: "ComplexPlot" link: "https://reference.wolfram.com/language/ref/ComplexPlot.en.md" - title: "ComplexPlot3D" link: "https://reference.wolfram.com/language/ref/ComplexPlot3D.en.md" - title: "ComplexContourPlot" link: "https://reference.wolfram.com/language/ref/ComplexContourPlot.en.md" - title: "ComplexRegionPlot" link: "https://reference.wolfram.com/language/ref/ComplexRegionPlot.en.md" - title: "StreamPlot3D" link: "https://reference.wolfram.com/language/ref/StreamPlot3D.en.md" --- # ComplexStreamPlot ComplexStreamPlot[f, {z, zmin, zmax}] generates a streamline plot of the vector field {Re[f], Im[f]} over the complex rectangle with corners zmin and zmax. ## Details and Options * ``ComplexStreamPlot`` plots streamlines that show the local direction of the complex vector field at each point, effectively solving the differential equation 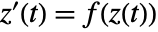$z'(t)=f(z(t))$ and then plotting 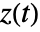$z(t)$. [image] * ``ComplexStreamPlot`` by default shows enough streamlines to achieve a roughly uniform density throughout the plot and shows no background scalar field. * No streamlines are shown at any positions for which ``f`` etc. do not evaluate to a complex number. * ``ComplexStreamPlot[f, {z, n}]`` is equivalent to ``ComplexStreamPlot[f, {z, -n - n I, n + n I}]``. * ``ComplexStreamPlot`` has attribute ``HoldAll`` and evaluates ``f`` etc. only after assigning specific numerical values to ``z``. In some cases, it may be more efficient to use ``Evaluate`` to evaluate ``f`` symbolically first. * ``ComplexStreamPlot`` has the same options as ``Graphics``, with the following additions and changes: [] | | | | | --------------------------- | ----------------- | -------------------------------------------------------- | | AspectRatio | 1 | ratio of height to width | | EvaluationMonitor | None | expression to evaluate at every function evaluation | | Frame | True | whether to draw a frame around the plot | | FrameTicks | Automatic | frame tick marks | | Method | Automatic | methods to use for the plot | | PerformanceGoal | \$PerformanceGoal | aspects of performance to try to optimize | | PlotLegends | None | legends to include | | PlotRange | {Full, Full} | range of x, y values to include | | PlotRangePadding | Automatic | how much to pad the range of values | | PlotTheme | \$PlotTheme | overall theme for the plot | | RegionBoundaryStyle | Automatic | how to style plot region boundaries | | RegionFillingStyle | Automatic | how to style plot region interiors | | RegionFunction | (True&) | determine what region to include | | StreamColorFunction | Automatic | how to color streamlines | | StreamColorFunctionScaling | True | whether to scale the argument to StreamColorFunction | | StreamMarkers | Automatic | shape to use for streams | | StreamPoints | Automatic | determine number, placement and closeness of streamlines | | StreamScale | Automatic | determine sizes and segmenting of individual streamlines | | StreamStyle | Automatic | how to draw streamlines | | WorkingPrecision | MachinePrecision | precision to use in internal computations | * Common stream markers include: | | | | | ------- | --------- | ------------------------------------------- | | [image] | "Segment" | line segment aligned in the field direction | | [image] | "PinDart" | pin dart aligned along the field | | [image] | "Dart" | dart-shaped marker | | [image] | "Drop" | drop-shaped marker | * The arguments supplied to functions in ``RegionFunction`` are 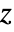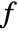$z$, $f$. Functions in ``ColorFunction`` are by default supplied with scaled versions of ``Re[z]``, ``Im[z]``, ``Abs[z]``, ``Arg[z]``, ``Re[f]``, ``Im[f]``, ``Abs[f]``, ``Arg[f]``. ### List of all options | | | | | -------------------------- | ----------------- | ---------------------------------------------------------------------------------- | | AlignmentPoint | Center | the default point in the graphic to align with | | AspectRatio | 1 | ratio of height to width | | Axes | False | whether to draw axes | | AxesLabel | None | axes labels | | AxesOrigin | Automatic | where axes should cross | | AxesStyle | {} | style specifications for the axes | | Background | None | background color for the plot | | BaselinePosition | Automatic | how to align with a surrounding text baseline | | BaseStyle | {} | base style specifications for the graphic | | ContentSelectable | Automatic | whether to allow contents to be selected | | CoordinatesToolOptions | Automatic | detailed behavior of the coordinates tool | | Epilog | {} | primitives rendered after the main plot | | EvaluationMonitor | None | expression to evaluate at every function evaluation | | FormatType | TraditionalForm | the default format type for text | | Frame | True | whether to draw a frame around the plot | | FrameLabel | None | frame labels | | FrameStyle | {} | style specifications for the frame | | FrameTicks | Automatic | frame tick marks | | FrameTicksStyle | {} | style specifications for frame ticks | | GridLines | None | grid lines to draw | | GridLinesStyle | {} | style specifications for grid lines | | ImageMargins | 0. | the margins to leave around the graphic | | ImagePadding | All | what extra padding to allow for labels etc. | | ImageSize | Automatic | the absolute size at which to render the graphic | | LabelStyle | {} | style specifications for labels | | Method | Automatic | methods to use for the plot | | PerformanceGoal | \$PerformanceGoal | aspects of performance to try to optimize | | PlotLabel | None | an overall label for the plot | | PlotLegends | None | legends to include | | PlotRange | {Full, Full} | range of x, y values to include | | PlotRangeClipping | False | whether to clip at the plot range | | PlotRangePadding | Automatic | how much to pad the range of values | | PlotRegion | Automatic | the final display region to be filled | | PlotTheme | \$PlotTheme | overall theme for the plot | | PreserveImageOptions | Automatic | whether to preserve image options when displaying new versions of the same graphic | | Prolog | {} | primitives rendered before the main plot | | RegionBoundaryStyle | Automatic | how to style plot region boundaries | | RegionFillingStyle | Automatic | how to style plot region interiors | | RegionFunction | (True&) | determine what region to include | | RotateLabel | True | whether to rotate y labels on the frame | | StreamColorFunction | Automatic | how to color streamlines | | StreamColorFunctionScaling | True | whether to scale the argument to StreamColorFunction | | StreamMarkers | Automatic | shape to use for streams | | StreamPoints | Automatic | determine number, placement and closeness of streamlines | | StreamScale | Automatic | determine sizes and segmenting of individual streamlines | | StreamStyle | Automatic | how to draw streamlines | | Ticks | Automatic | axes ticks | | TicksStyle | {} | style specifications for axes ticks | | WorkingPrecision | MachinePrecision | precision to use in internal computations | --- ## Examples (108) ### Basic Examples (1) Visualize a complex function of a complex variable $f(z)$ as a stream plot: ```wl In[1]:= ComplexStreamPlot[z^2, {z, -2 - 2I, 2 + 2I}] Out[1]= [image] ``` ### Scope (22) #### Sampling (8) Plot a complex functions with streamlines placed with specified densities: ```wl In[1]:= Table[ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, PlotLabel -> p, StreamPoints -> p], {p, {Coarse, Medium, Automatic, Fine}}] Out[1]= [image] ``` --- Plot the streamlines that go through a set of complex seed points: ```wl In[1]:= ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, StreamPoints -> {1 + I, 1 - I, 2, -2, 2 + 2I, -2 - 2I}] Out[1]= [image] ``` --- Use both automatic and explicit seeding with styles for explicitly seeded streamlines: ```wl In[1]:= ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, StreamPoints -> {{{1 + I, Red}, {1 - I, Green}, Automatic}}, StreamColorFunction -> None] Out[1]= [image] ``` --- Plot streamlines over a specified complex region: ```wl In[1]:= ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, RegionFunction -> Function[{z, f}, Abs[z] < 3]] Out[1]= [image] ``` --- Plot two functions together: ```wl In[1]:= ComplexStreamPlot[{z^2, Conjugate[z^2]}, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> None] Out[1]= [image] ``` --- Use a specific number of mesh lines: ```wl In[1]:= ComplexStreamPlot[z^2 + 1, {z, -2 - 2I, 2 + 2I}, Mesh -> 5] Out[1]= [image] ``` --- Specify specific mesh lines: ```wl In[1]:= ComplexStreamPlot[z^2 + 1, {z, -2 - 2I, 2 + 2I}, Mesh -> {{1, 2, 3, 4, 5}}] Out[1]= [image] ``` --- Use ``Evaluate`` to evaluate the vector field symbolically before numeric assignment: ```wl In[1]:= ComplexStreamPlot[Evaluate[D[z^3 + z, z]], {z, -2 - 2I, 2 + 2I}] Out[1]= [image] ``` #### Presentation (14) Specify different dashings and arrowheads by setting to ``StreamScale`` : ```wl In[1]:= Table[ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> ToString@s, StreamScale -> s], {s, {Automatic, None, Full}}] Out[1]= [image] ``` --- Plot the streamlines with arrows colored according to the modulus of the function: ```wl In[1]:= ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Hue] Out[1]= [image] ``` --- Apply a variety of streamline markers: ```wl In[1]:= Table[ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, StreamMarkers -> s], {s, {"Toothpick", "Dart", "Drop"}}] Out[1]= [image] ``` --- Use a theme with axes and a different default color: ```wl In[1]:= ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, PlotTheme -> "Business"] Out[1]= [image] ``` --- Override the style from the theme: ```wl In[1]:= ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, PlotTheme -> "Business", StreamStyle -> Red, StreamColorFunction -> None] Out[1]= [image] ``` --- Change the color function: ```wl In[1]:= ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> "Rainbow"] Out[1]= [image] ``` --- Specify a uniform color for the streamlines: ```wl In[1]:= ComplexStreamPlot[Exp[2z], {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> None, StreamStyle -> Orange] Out[1]= [image] ``` --- Specify mesh lines with different styles: ```wl In[1]:= ComplexStreamPlot[z Exp[2z], {z, -2 - 2I, 2 + 2I}, Mesh -> {{{1, Thick}, {2, Green}, {4, {Thick, Red, Dashed}}}}, MeshStyle -> Opacity[1]] Out[1]= [image] ``` --- Specify global mesh line styles: ```wl In[1]:= Table[ComplexStreamPlot[z Exp[z], {z, -2 - 2I, 2 + 2I}, Mesh -> 10, MeshStyle -> s], {s, {Red, Thick, Directive[Red, Dashed]}}] Out[1]= [image] ``` --- Shade mesh regions cyclically: ```wl In[1]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, Mesh -> 10, MeshShading -> {Red, Yellow, Green, None}] Out[1]= [image] ``` --- Apply a variety of styles to region boundaries: ```wl In[1]:= regionFn = Function[{z, f}, 4 < Abs[f] < 6 || 0 < Abs[f] < 2]; In[2]:= Table[ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn, RegionBoundaryStyle -> b], {b, {Red, Thick, Directive[Red, Dashed]}}] Out[2]= [image] ``` --- Add a legend indicating the modulus of the function: ```wl In[1]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, PlotLegends -> Automatic] Out[1]= [image] ``` --- Use the functions as legend labels: ```wl In[1]:= ComplexStreamPlot[{z Sin[z], z Cos[z]}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> "Expressions", StreamColorFunction -> None] Out[1]= [image] ``` --- Use explicit labels for each vector field: ```wl In[1]:= ComplexStreamPlot[{z Sin[z], z Cos[z]}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> {"first", "second"}, StreamColorFunction -> None] Out[1]= [image] ``` ### Options (60) #### Background (1) Use a colored background: ```wl In[1]:= ComplexStreamPlot[z^2, {z, -2 - 2I, 2 + 2I}, Background -> LightGray] Out[1]= [image] ``` #### EvaluationMonitor (2) Show where the vector field function is sampled: ```wl In[1]:= ComplexListPlot[Reap[ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, EvaluationMonitor :> Sow[z]]][[-1, 1]]] Out[1]= [image] ``` --- Count the number of times the vector field function is evaluated: ```wl In[1]:= Block[{k = 0}, ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, EvaluationMonitor :> k++];k] Out[1]= 4639 ``` #### PerformanceGoal (2) Generate a higher-quality plot: ```wl In[1]:= ComplexStreamPlot[Sinc[3z], {z, -2 - 2I, 2 + 2I}, PerformanceGoal -> "Quality"] Out[1]= [image] ``` --- Emphasize performance, possibly at the cost of quality: ```wl In[1]:= ComplexStreamPlot[Sinc[3z], {z, -2 - 2I, 2 + 2I}, PerformanceGoal -> "Speed"] Out[1]= [image] ``` #### PlotLegends (7) No legends are included, by default: ```wl In[1]:= ComplexStreamPlot[Sinc[z], {z, -2 - 2I, 2 + 2I}] Out[1]= [image] ``` --- Include a legend that indicates the modulus of the function: ```wl In[1]:= ComplexStreamPlot[Sinc[z], {z, -2 - 2I, 2 + 2I}, PlotLegends -> Automatic] Out[1]= [image] ``` --- Include a legend to distinguish two functions: ```wl In[1]:= ComplexStreamPlot[{Sinc[z], z}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> {"one", "two"}, StreamColorFunction -> None] Out[1]= [image] ``` --- Control the placement of the legend: ```wl In[1]:= ComplexStreamPlot[{Sinc[z], z}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> Placed[{"one", "two"}, Below], StreamColorFunction -> None] Out[1]= [image] ``` --- Use the functions as the legend text: ```wl In[1]:= ComplexStreamPlot[{Sinc[z], z}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> "Expressions", StreamColorFunction -> None] Out[1]= [image] ``` --- Use placeholder text: ```wl In[1]:= ComplexStreamPlot[{Sinc[z], z}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> Automatic, StreamColorFunction -> None] Out[1]= [image] ``` --- Change the appearance of the legend: ```wl In[1]:= ComplexStreamPlot[{Sinc[z], z}, {z, -2 - 2I, 2 + 2I}, PlotLegends -> SwatchLegend["Expressions", LegendMarkerSize -> {40, 10}], StreamColorFunction -> None] Out[1]= [image] ``` #### PlotRange (5) The full plot range is used by default: ```wl In[1]:= ComplexStreamPlot[z^3, {z, -2 - 2I, 2 + 2I}, PlotRange -> Full] Out[1]= [image] ``` --- Specify an explicit limit for both the $\Re(z)$ and $\Im(z)$ ranges: ```wl In[1]:= ComplexStreamPlot[z^3, {z, -2 - 2I, 2 + 2I}, PlotRange -> 1] Out[1]= [image] ``` --- Specify an explicit $\Re(z)$ range: ```wl In[1]:= ComplexStreamPlot[z^3, {z, -2 - 2I, 2 + 2I}, PlotRange -> {{-1, 1}, Automatic}] Out[1]= [image] ``` --- Specify an explicit $\Im(z)$ range: ```wl In[1]:= ComplexStreamPlot[z^3, {z, -2 - 2I, 2 + 2I}, PlotRange -> {Full, {-1, 2}}] Out[1]= [image] ``` --- Specify different $\Re(z)$ and $\Im(z)$ ranges: ```wl In[1]:= ComplexStreamPlot[z^3, {z, -2 - 2I, 2 + 2I}, PlotRange -> {{-2, 1}, {0, 1}}] Out[1]= [image] ``` #### PlotTheme (3) Use a theme with simpler ticks and brighter colors: ```wl In[1]:= ComplexStreamPlot[{Sqrt[z], z^3}, {z, -2 - 2I, 2 + 2I}, PlotTheme -> "Web"] Out[1]= [image] ``` --- Use a theme with automatic legends and dense streamlines: ```wl In[1]:= ComplexStreamPlot[{Sqrt[z], z^3}, {z, -2 - 2I, 2 + 2I}, PlotTheme -> "Detailed", StreamColorFunction -> None] Out[1]= [image] ``` --- Change the stream styles: ```wl In[1]:= ComplexStreamPlot[{Sqrt[z], z^3}, {z, -2 - 2I, 2 + 2I}, PlotTheme -> "Detailed", StreamStyle -> {Red, Blue}, StreamColorFunction -> None] Out[1]= [image] ``` #### RegionBoundaryStyle (1) By default, region boundaries are styled automatically: ```wl In[1]:= regionFn = Function[{z, f}, n = Norm[z];4 < n < 6 || 0 < n < 2]; In[2]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn] Out[2]= [image] ``` Apply a variety of styles to region boundaries: ```wl In[3]:= Table[ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn, RegionBoundaryStyle -> b], {b, {Red, Thick, Directive[Red, Dashed]}}] Out[3]= [image] ``` #### RegionFillingStyle (1) By default, regions are filled: ```wl In[1]:= regionFn = Function[{z, f}, n = Norm[z];4 < n < 6 || 0 < n < 2]; In[2]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn] Out[2]= [image] ``` Show no filling: ```wl In[3]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn, RegionFillingStyle -> None] Out[3]= [image] ``` Choose a different filling: ```wl In[4]:= ComplexStreamPlot[z Sin[z], {z, -2 - 2I, 2 + 2I}, RegionFunction -> regionFn, RegionFillingStyle -> Yellow] Out[4]= [image] ``` #### RegionFunction (3) Plot streamlines only over a disk: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, RegionFunction -> Function[{z, f}, Abs[z] < 2]] Out[1]= [image] ``` --- Plot streamlines only over regions where the modulus of the function exceeds a given threshold: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, RegionFunction -> Function[{z, f}, Abs[f] > 2]] Out[1]= [image] ``` --- Use a logical combination of conditions: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, RegionFunction -> Function[{z, f}, Abs[f] < 1 || Abs[f] > 6]] Out[1]= [image] ``` #### StreamColorFunction (5) Color streamlines according to the modulus of the function: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Hue] Out[1]= [image] ``` --- Use any named color gradient from ``ColorData``: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> "Rainbow"] Out[1]= [image] ``` --- Use ``ColorData`` for predefined color gradients: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Function[{z, f}, ColorData["AvocadoColors"][Arg[z]]]] Out[1]= [image] ``` --- Specify a color function that blends two colors by $\Re(z)$ : ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Function[{z, f}, Blend[{Blue, Red}, Re[z]]]] Out[1]= [image] ``` --- Use ``StreamColorFunctionScaling -> False`` to get unscaled values: ```wl In[1]:= ComplexStreamPlot[z^4 + z^2, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Hue, StreamColorFunctionScaling -> False] Out[1]= [image] ``` #### StreamColorFunctionScaling (3) By default, scaled values are used: ```wl In[1]:= ComplexStreamPlot[z, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Hue] Out[1]= [image] ``` --- Use ``StreamColorFunctionScaling -> False`` to get unscaled values: ```wl In[1]:= ComplexStreamPlot[z, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Hue, StreamColorFunctionScaling -> False] Out[1]= [image] ``` --- Explicitly specify the scaling for each color function argument: ```wl In[1]:= ComplexStreamPlot[z, {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> Function[{z, f}, Hue[Abs[f], Abs[z], 1]], StreamColorFunctionScaling -> {True, False}] Out[1]= [image] ``` #### StreamMarkers (8) Streamlines are drawn as arrows by default: ```wl In[1]:= ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}] Out[1]= [image] ``` --- Use a named appearance to draw the streamlines: ```wl In[1]:= ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamMarkers -> "Drop"] Out[1]= [image] ``` --- Use different markers for different vector fields: ```wl In[1]:= ComplexStreamPlot[{z, z^2 - Conjugate[z]}, {z, -2 - 2I, 2 + 2I}, StreamMarkers -> {"Drop", "Dart"}, StreamColorFunction -> None] Out[1]= [image] ``` --- Use named styles: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamStyle -> s], {s, {"Segment", "Line"}}] Out[1]= [image] ``` --- Named arrow styles: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> {Full, All, 0.05}, StreamStyle -> s], {s, {"Arrow", "ArrowArrow", "CircleArrow"}}] Out[1]= {[image], [image], [image]} ``` --- Named dot styles: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> {Full, All, 0.03}, StreamStyle -> s], {s, {"BarDot", "Dot", "DotArrow", "DotDot"}}] Out[1]= [image] ``` --- Named pointer styles: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> {Full, All, 0.03}, StreamStyle -> s], {s, {"Drop", "BackwardPointer", "Pointer", "Toothpick"}}] Out[1]= [image] ``` --- Named dart styles: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> {Full, All, 0.03}, StreamStyle -> s], {s, {"Dart", "PinDart", "DoubleDart"}}] Out[1]= [image] ``` #### StreamPoints (5) Specify a specific maximum number of streamlines: ```wl In[1]:= ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamPoints -> 10] Out[1]= [image] ``` --- Use symbolic names to specify the number of streamlines: ```wl In[1]:= Table[ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamPoints -> p, PlotLabel -> p], {p, {Automatic, Coarse, Fine}}] Out[1]= [image] ``` --- Use both automatic and explicit seeding with styles for explicitly seeded streamlines: ```wl In[1]:= ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamColorFunction -> None, StreamPoints -> {{{{1, 1}, Red}, {{-1, -1}, Green}, Automatic}}] Out[1]= [image] ``` --- Specify the minimum distance between streamlines: ```wl In[1]:= Table[ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamPoints -> {Automatic, d}], {d, {Automatic, 1, Scaled[0.05]}}] Out[1]= [image] ``` --- Specify the minimum distance between streamlines at the start and end of a streamline: ```wl In[1]:= Table[ComplexStreamPlot[z^2 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamPoints -> {Automatic, d}], {d, {Automatic, {Scaled[0.1], Scaled[0.5]}}}] Out[1]= [image] ``` #### StreamScale (9) Create full streamlines without segmentation: ```wl In[1]:= ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamScale -> Full] Out[1]= [image] ``` --- Use curves for streamlines: ```wl In[1]:= ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamScale -> None] Out[1]= [image] ``` --- Use symbolic names to control the lengths of streamlines: ```wl In[1]:= Table[ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> s], {s, {Tiny, Large}}] Out[1]= [image] ``` --- Specify segment lengths: ```wl In[1]:= Table[ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> s, StreamScale -> s], {s, {0.1, 0.2, 0.4}}] Out[1]= [image] ``` --- Specify an explicit dashing pattern for streamlines: ```wl In[1]:= ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamScale -> {{0.1, 0.1}, Automatic}] Out[1]= [image] ``` --- Specify the number of points rendered on each streamline segment: ```wl In[1]:= Table[ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> n, StreamScale -> {Full, n}], {n, {12, 24, All}}] Out[1]= {[image], [image], [image]} ``` --- Specify absolute aspect ratios relative to the longest line segment: ```wl In[1]:= Table[ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> a, StreamScale -> {Automatic, Automatic, a}], {a, {.02, .04}}] Out[1]= [image] ``` --- Specify relative aspect ratios relative to each line segment: ```wl In[1]:= Table[ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, PlotLabel -> a, StreamScale -> {Automatic, Automatic, a}], {a, {Scaled[0.5], Scaled[1], Scaled[1.5]}}] Out[1]= [image] ``` --- Scale the length of the arrows by the $\Re(z)$ : ```wl In[1]:= ComplexStreamPlot[z^3 - Conjugate[z], {z, -2 - 2I, 2 + 2I}, StreamScale -> {Automatic, 2, Automatic, Function[{z, f}, Re[z]]}] Out[1]= [image] ``` #### StreamStyle (5) ``StreamColorFunction`` has precedence over ``StreamStyle`` for colors: ```wl In[1]:= ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, StreamStyle -> Red] Out[1]= [image] ``` --- Use ``StreamColorFunction`` -> ``None`` to specify colors with ``StreamStyle`` : ```wl In[1]:= ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, StreamStyle -> Red, StreamColorFunction -> None] Out[1]= [image] ``` --- Apply a variety of styles to the streamlines: ```wl In[1]:= Table[ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, StreamStyle -> s, StreamColorFunction -> None], {s, {Orange, Thick, Directive[Orange, Dashed]}}] Out[1]= [image] ``` --- Specify a custom arrowhead: ```wl In[1]:= ComplexStreamPlot[z^2 Log[z], {z, -2 - 2I, 2 + 2I}, StreamScale -> Full, StreamStyle -> Arrowheads[{{0.03, Automatic, Graphics[Circle[]]}}]] Out[1]= [image] ``` --- Set the style for multiple functions: ```wl In[1]:= ComplexStreamPlot[{z, z^2 Log[z]}, {z, -2 - 2I, 2 + 2I}, StreamStyle -> {Red, Blue}, StreamColorFunction -> None] Out[1]= [image] ``` ### Applications (10) #### Basic Applications (1) Plot a function with a simple zero: ```wl In[1]:= ComplexStreamPlot[z, {z, 5}] Out[1]= [image] ``` Shift the function to the left by 1: ```wl In[2]:= ComplexStreamPlot[z + 1, {z, 5}] Out[2]= [image] ``` Plot a function with a double zero: ```wl In[3]:= ComplexStreamPlot[z ^ 2, {z, 5}] Out[3]= [image] ``` Plot a square root function: ```wl In[4]:= ComplexStreamPlot[Sqrt[z], {z, 5}] Out[4]= [image] ``` Plot a trigonometric function: ```wl In[5]:= ComplexStreamPlot[Sin[z], {z, 5}] Out[5]= [image] ``` Plot a transcendental function: ```wl In[6]:= ComplexStreamPlot[Log[z], {z, 5}] Out[6]= [image] ``` Plot a function with a simple pole: ```wl In[7]:= ComplexStreamPlot[1 / z, {z, 5}] Out[7]= [image] ``` Plot a function with a double pole: ```wl In[8]:= ComplexStreamPlot[1 / z ^ 2, {z, 5}] Out[8]= [image] ``` #### Other Applications (9) Streamlines that diverge from a point indicate a simple zero: ```wl In[1]:= ComplexStreamPlot[z, {z, -3 - 3I, 3 + 3I}] Out[1]= [image] ``` Streamlines can also converge at a simple zero: ```wl In[2]:= ComplexStreamPlot[-z, {z, -3 - 3I, 3 + 3I}] Out[2]= [image] ``` --- With $z=x+i y$, the real vector field corresponding to the complex function $z^2$ is $\left\{x^2-y^2,2 x y\right\}$, and the trajectories that follow the field satisfy the differential equation $\frac{d y}{d x}=\frac{2 x y}{x^2-y^2}$. The implicit solution is $c y+x^2+y^2=0$ for real $c$, which corresponds to a family of circles that are tangent to the real axis at the origin: ```wl In[1]:= Show[ContourPlot[(x^2/y) + y, {x, -3, 3}, {y, -3, 3}, ContourShading -> None, ContourStyle -> Red, Contours -> Range[-8, 8]], ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, StreamColorFunction -> None]] Out[1]= [image] ``` In polar coordinates, the trajectories are $r=c \sin (\theta )$ for any real $c$ : ```wl In[2]:= Show[PolarPlot[Evaluate@Table[c Sin[θ], {c, -3, 3}], {θ, 0, π}, PlotStyle -> Red], ComplexStreamPlot[z^2, {z, -3 - 3I, 3 + 3I}, StreamColorFunction -> None]] Out[2]= [image] ``` More generally, for $z^n$ where $n$ is an integer, the streamlines follow $r^n=c \sin (\theta (n-1))$ for constant $c$ : ```wl In[3]:= n = 4; In[4]:= Show[PolarPlot[Evaluate@Table[c Surd[Sin[(n - 1)θ], n - 1], {c, -3, 3}], {θ, 0, π}, PlotStyle -> Red], ComplexStreamPlot[z^n, {z, -3 - 3I, 3 + 3I}, StreamColorFunction -> None]] Out[4]= [image] In[5]:= n = -4; In[6]:= Show[PolarPlot[Evaluate@Table[c Surd[Sin[(n - 1)θ], n - 1], {c, -3, 3}], {θ, 0, π}, PlotStyle -> Red], ComplexStreamPlot[z^n, {z, -3 - 3I, 3 + 3I}, StreamColorFunction -> None], PlotRange -> 3] Out[6]= [image] ``` --- Near a zero of order $n>1$, the streamlines form loops that start and end at the zero in $n+1$ directions: ```wl In[1]:= n = 3; In[2]:= Show[ComplexPlot[z^n, {z, -3 - 3I, 3 + 3I}, ColorFunction -> None], ComplexStreamPlot[z^n, {z, -3 - 3I, 3 + 3I}, StreamStyle -> White, StreamColorFunction -> None, StreamScale -> Large]] Out[2]= [image] ``` --- Near a pole of order $n$, the streamlines converge to the pole from $n+1$ directions and diverge from the pole from $n+1$ directions: ```wl In[1]:= n = 2; In[2]:= Show[ComplexPlot[1 / z^n, {z, -3 - 3I, 3 + 3I}, ColorFunction -> None], ComplexStreamPlot[1 / z^n, {z, -3 - 3I, 3 + 3I}, StreamStyle -> White, StreamColorFunction -> None, StreamScale -> Large]] Out[2]= [image] ``` --- The function $\frac{z^2+2 z-3}{z^4-6 z^3+18 z^2-54 z+81}$ has simple zeros at $z=-3$ and $z=1$, poles of order 1 at $z=i \pm 3$, and a pole of order 2 at $z=3$ : ```wl In[1]:= ComplexStreamPlot[(z^2 + 2 z - 3/z^4 - 6 z^3 + 18 z^2 - 54 z + 81), {z, -5 - 5I, 5 + 5I}] Out[1]= [image] ``` --- Near an essential singularity, the streamlines vary wildly: ```wl In[1]:= ComplexStreamPlot[Exp[-5 / z], {z, -1 - I, 1 + I}] Out[1]= [image] ``` --- Plot a function and its derivatives: ```wl In[1]:= ComplexStreamPlot[#, {z, -1 - I, 1 + I}]& /@ NestList[D[#, z]&, z^3, 3] Out[1]= [image] ``` --- Generate a Pólya plot: ```wl In[1]:= ComplexStreamPlot[Conjugate[z^2], {z, -2 - 2I, 2 + 2I}] Out[1]= [image] ``` --- Let $F(z)=\phi (x,y)+i \psi (x,y)$ be a complex potential for an ideal fluid flow. Then $\phi$ is the velocity potential, $\psi$ is the stream function, and the fluid velocity field is $\nabla \phi$. By the Cauchy–Riemann equations, $F'(z)=\phi _x(x,y)+i \psi _x(x,y)=\phi _x(x,y)-i \phi _y(x,y)$, so you can generate a stream plot with the conjugate of $F'(z)$. Show streamlines for flow around a cylinder with circulation: ```wl In[1]:= F = z + (1/z) + I Log[z]; In[2]:= ComplexStreamPlot[Evaluate[Conjugate[D[F, z]]], {z, -2 - 2I, 2 + 2I}, Epilog -> {Circle[]}, StreamScale -> Full, StreamStyle -> "Line"] Out[2]= [image] ``` Show streamlines for flow external to a corner: ```wl In[3]:= F = (-I z)^2 / 3 - (-z)^2 / 3; In[4]:= ComplexStreamPlot[Evaluate[Conjugate[D[F, z]]], {z, -2 - 2I, 2 + 2I}, StreamScale -> Full, StreamStyle -> "Line", RegionFunction -> Function[{z, f}, Arg[z] < -π / 2 || Arg[z] > 0]] Out[4]= [image] ``` ### Properties & Relations (15) ``ComplexStreamPlot`` is a special case of ``StreamPlot`` : ```wl In[1]:= {ComplexStreamPlot[Sin[z], {z, 4}], StreamPlot[ReIm[Sin[x + I * y]], {x, -4 , 4}, {y, -4, 4}]} Out[1]= {[image], [image]} ``` --- ``ComplexVectorPlot`` plots complex numbers as vectors: ```wl In[1]:= ComplexVectorPlot[Log[z], {z, 3}] Out[1]= [image] ``` ``ComplexVectorPlot`` is a special case of ``VectorPlot`` : ```wl In[2]:= VectorPlot[ReIm[Log[x + I y]], {x, -3, 3}, {y, -3, 3}] Out[2]= [image] ``` --- Use ``VectorDisplacementPlot`` to visualize the effect of a complex function on a specified region: ```wl In[1]:= VectorDisplacementPlot[ReIm[Sin[x + I y]], {x, y}∈Annulus[], VectorPoints -> Automatic, VectorSizes -> Full] Out[1]= [image] ``` --- Use ``VectorPlot3D`` and ``StreamPlot3D`` to visualize 3D vector fields: ```wl In[1]:= {VectorPlot3D[{z, x, y}, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}], StreamPlot3D[{z, x, y}, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}]} Out[1]= {[image], [image]} ``` --- ``ComplexContourPlot`` plots curves over the complexes: ```wl In[1]:= ComplexContourPlot[Abs[Log[z]] == 1, {z, 3}] Out[1]= [image] ``` --- ``ComplexRegionPlot`` plots regions over the complexes: ```wl In[1]:= ComplexRegionPlot[Abs[Log[z]] < 1, {z, 3}] Out[1]= [image] ``` --- ``ComplexPlot`` shows the argument and magnitude of a function using color: ```wl In[1]:= ComplexPlot[Log[z], {z, 3}] Out[1]= [image] ``` --- Use ``ComplexPlot3D`` to use the $z$ axis for the magnitude: ```wl In[1]:= ComplexPlot3D[Log[z], {z, 3}] Out[1]= [image] ``` --- Use ``ComplexArrayPlot`` for arrays of complex numbers: ```wl In[1]:= ComplexArrayPlot[Table[x ^ 3 + I y ^ 2, {x, -2, 2, 0.1}, {y, -2, 2, 0.1}]] Out[1]= [image] ``` --- Use ``ReImPlot`` and ``AbsArgPlot`` to plot complex values over the real numbers: ```wl In[1]:= ReImPlot[Log[x], {x, -3, 3}] Out[1]= [image] In[2]:= AbsArgPlot[Log[x], {x, -3, 3}] Out[2]= [image] ``` --- Use ``ComplexListPlot`` to show the location of complex numbers in the plane: ```wl In[1]:= ComplexListPlot[RandomComplex[{-3 - 3I, 3 + 3I}, 100]] Out[1]= [image] ``` --- Use ``ListVectorPlot`` for plotting data: ```wl In[1]:= data = Table[ReIm[(x + I y)^2], {x, -3, 3, 0.2}, {y, -3, 3, 0.2}]; In[2]:= ListVectorPlot[data] Out[2]= [image] ``` Use ``ListStreamPlot`` to plot streams instead of vectors: ```wl In[3]:= ListStreamPlot[data] Out[3]= [image] ``` --- Use ``VectorDensityPlot`` to add a density plot of a scalar field: ```wl In[1]:= VectorDensityPlot[ReIm[(x + I y)^2], {x, -3, 3}, {y, -3, 3}] Out[1]= [image] ``` Use ``StreamDensityPlot`` to use streams instead of vectors: ```wl In[2]:= StreamDensityPlot[ReIm[(x + I y)^2], {x, -3, 3}, {y, -3, 3}] Out[2]= [image] ``` --- Use ``ListVectorDensityPlot`` to generate a density plot of a scalar field based on data: ```wl In[1]:= data = Table[{{x, y}, ReIm[(x + I y)^2 + 1]}, {x, -3, 3, 0.2}, {y, -3, 3, 0.2}]; In[2]:= ListVectorDensityPlot[data] Out[2]= [image] ``` Use ``ListStreamDensityPlot`` to plot streams instead of vectors: ```wl In[3]:= ListStreamDensityPlot[data] Out[3]= [image] ``` --- Use ``LineIntegralConvolutionPlot`` to plot the line integral convolution of a vector field: ```wl In[1]:= LineIntegralConvolutionPlot[ReIm[(x + I y)^3], {x, -3, 3}, {y, -3, 3}] Out[1]= [image] ``` ## See Also * [`ComplexVectorPlot`](https://reference.wolfram.com/language/ref/ComplexVectorPlot.en.md) * [`StreamPlot`](https://reference.wolfram.com/language/ref/StreamPlot.en.md) * [`VectorPlot`](https://reference.wolfram.com/language/ref/VectorPlot.en.md) * [`ListStreamPlot`](https://reference.wolfram.com/language/ref/ListStreamPlot.en.md) * [`ComplexPlot`](https://reference.wolfram.com/language/ref/ComplexPlot.en.md) * [`ComplexPlot3D`](https://reference.wolfram.com/language/ref/ComplexPlot3D.en.md) * [`ComplexContourPlot`](https://reference.wolfram.com/language/ref/ComplexContourPlot.en.md) * [`ComplexRegionPlot`](https://reference.wolfram.com/language/ref/ComplexRegionPlot.en.md) * [`StreamPlot3D`](https://reference.wolfram.com/language/ref/StreamPlot3D.en.md) ## Related Guides * [Complex Visualization](https://reference.wolfram.com/language/guide/ComplexVisualization.en.md) * [Vector Visualization](https://reference.wolfram.com/language/guide/VectorVisualization.en.md) ## History * [Introduced in 2020 (12.1)](https://reference.wolfram.com/language/guide/SummaryOfNewFeaturesIn121.en.md) \| [Updated in 2020 (12.2)](https://reference.wolfram.com/language/guide/SummaryOfNewFeaturesIn122.en.md)