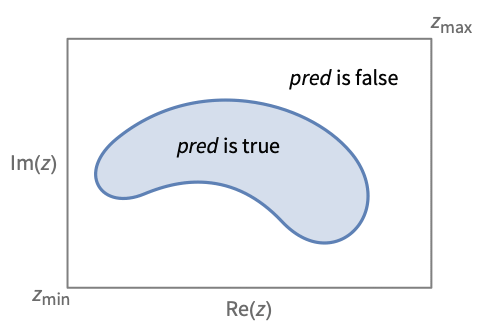
ComplexRegionPlot[pred,{z,zmin,zmax}]
makes a plot showing the region in the complex plane for which pred is True.
ComplexRegionPlot[{pred1,pred2,…},{z,zmin,zmax}]
plots regions given by the multiple predicates predi.






ComplexRegionPlot
ComplexRegionPlot[pred,{z,zmin,zmax}]
makes a plot showing the region in the complex plane for which pred is True.
ComplexRegionPlot[{pred1,pred2,…},{z,zmin,zmax}]
plots regions given by the multiple predicates predi.
Details and Options






- The predicate predi can be any logical combination of inequalities. The predi will typically involve functions like Re, Im, Abs and Arg that extract real components from complex numbers for comparison purposes.
- The region plotted by ComplexRegionPlot can contain disconnected parts.
- ComplexRegionPlot[pred,{z,n}] is equivalent to ComplexRegionPlot[pred,{z,-n-n I,n+n I}].
- ComplexRegionPlot treats the variable z as local, effectively using Block.
- ComplexRegionPlot has attribute HoldAll and evaluates pred only after assigning specific numerical values to z. In some cases, it may be more efficient to use Evaluate to evaluate pred symbolically first.
- The following wrappers w can be used for the predi:
-
Annotation[predi,label] provide an annotation for the predi Button[predi,action] evaluate action when the curve for predi is clicked Callout[predi,label] label the region with a callout Callout[predi,label,pos] place the callout at relative position pos EventHandler[predi,events] define a general event handler for predi Hyperlink[predi,uri] make the region a hyperlink Labeled[predi,label] label the region Labeled[predi,label,pos] place the label at relative position pos Legended[predi,label] identify the region in a legend PopupWindow[predi,cont] attach a popup window to the region StatusArea[predi,label] display in the status area on mouseover Style[predi,styles] show the region using the specified styles Tooltip[predi,label] attach a tooltip to the region Tooltip[predi] use regions as tooltips - Wrappers w can be applied at multiple levels:
-
w[predi] wrap the predi w[{predi,…}] wrap a collection of predi w1[w2[…]] use nested wrappers - Callout, Labeled and Placed can use the following positions pos:
-
Automatic automatically placed labels Above, Below, Before, After positions around the region z position near z {pos,epos} epos in label placed at relative position pos of the region - ComplexRegionPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
AspectRatio 1 ratio of height to width BoundaryStyle Automatic the style for the boundary of each region ColorFunction Automatic how to color the interior of each region ColorFunctionScaling True whether to scale the argument to ColorFunction EvaluationMonitor None expression to evaluate at every function evaluation Frame True whether to draw a frame around the plot LabelingSize Automatic maximum size of callouts and labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh lines to draw MeshFunctions {#1&,#2&} what mesh lines to draw MeshShading None how to shade regions between mesh lines MeshStyle Automatic the style for mesh lines Method Automatic the method to use for refining regions PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabels None labels to use for curves PlotLegends None legends for regions PlotPoints Automatic initial number of sample points PlotRange Full the range of values to include in the plot PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotStyle Automatic graphics directives to specify the style for regions PlotTheme $PlotTheme overall theme for the plot TextureCoordinateFunction Automatic how to determine texture coordinates TextureCoordinateScaling True whether to scale arguments to TextureCoordinateFunction WorkingPrecision MachinePrecision the precision used in internal computations - Typical settings for PlotLegends include:
-
None no legend Automatic automatically determine the legend "Expressions" use f1, f2, … as the legend labels {lbl1,lbl2,…} use lbl1, lbl2, … as the legend labels Placed[lspec,…] specify placement for the legend - ComplexRegionPlot initially evaluates pred at a grid of equally spaced sample points specified by PlotPoints. Then it uses an adaptive algorithm to subdivide at most MaxRecursion times, attempting to find the boundaries of all regions in which pred is True.
- You should realize that since it uses only a finite number of sample points, it is possible for ComplexRegionPlot to miss regions in which pred is True. To check your results, you should try increasing the settings for PlotPoints and MaxRecursion.
- With the default setting PlotRange->Full, ComplexRegionPlot will explicitly include the full ranges zmin to zmax for z.
- ComplexRegionPlot can in general only find regions of positive measure; it cannot find regions that are just lines or points.
- The argument supplied to functions in MeshFunctions is z. ColorFunction and TextureCoordinateFunction are by default supplied with scaled versions of of Re[z], Im[z], Abs[z], Arg[z].
-
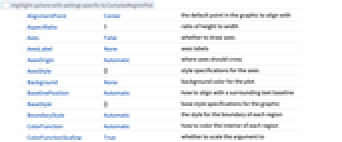
AlignmentPoint Center the default point in the graphic to align with AspectRatio 1 ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic BoundaryStyle Automatic the style for the boundary of each region ColorFunction Automatic how to color the interior of each region ColorFunctionScaling True whether to scale the argument to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot EvaluationMonitor None expression to evaluate at every function evaluation FormatType TraditionalForm the default format type for text Frame True whether to draw a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelingSize Automatic maximum size of callouts and labels LabelStyle {} style specifications for labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh lines to draw MeshFunctions {#1&,#2&} what mesh lines to draw MeshShading None how to shade regions between mesh lines MeshStyle Automatic the style for mesh lines Method Automatic the method to use for refining regions PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotLabels None labels to use for curves PlotLegends None legends for regions PlotPoints Automatic initial number of sample points PlotRange Full the range of values to include in the plot PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to specify the style for regions PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame TextureCoordinateFunction Automatic how to determine texture coordinates TextureCoordinateScaling True whether to scale arguments to TextureCoordinateFunction Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks WorkingPrecision MachinePrecision the precision used in internal computations
List of all options




Examples
open all close allBasic Examples (5)
Scope (23)
Sampling (3)
More points are sampled near the boundary of the region:
Use PlotPoints and MaxRecursion to control adaptive sampling:
Labeling and Legending (9)
Label regions with Labeled:
Place the labels in different positions:
Label regions with Callout:
Callout leader is turned off when label is inside the region:
Add a legend with PlotLegends:
Use editable placeholders in the legend:
Add legends with Legended:
Presentation (11)
Provide an explicit PlotStyle for the region:
Provide an explicit BoundaryStyle for the region boundary:
Add descriptive labels for the plot, the axes and the regions:
Use a combination of methods to label regions:
Use a legend for multiple regions:
Produce a legend with editable placeholders:
Use a legend for colored regions:
Style the areas between mesh lines:
Options (59)
BoundaryStyle (4)
Use None to show regions without any boundary:
ColorFunction (5)
Color regions by scaled Re[z], Im[z], Abs[z] or Arg[z]:
Named color functions use the scaled Arg[z] direction:
Color regions according to a function of ![]() :
:
ColorFunction has higher priority than PlotStyle:
ColorFunction has lower priority than MeshShading:
Mesh (7)
MeshFunctions (2)
MeshShading (4)
Use None to remove regions:
Lay a checkerboard pattern over a region:
MeshShading has a higher priority than PlotStyle:
MeshShading has a higher priority than ColorFunction:
MeshStyle (2)
PerformanceGoal (2)
PlotLabels (5)
Place the label above the region:
Place the label inside the region:
Use Callout to place the label:
PlotLegends (8)
Use legends for multiple regions:
Use automatic legends for a gradient colored region:
PlotLegends automatically picks up styles:
Use functions as legend texts:
Use Placed to change legend position:
Use SwatchLegend to change legend appearance:
PlotRange (2)
PlotStyle (5)
Regions are shown in light blue:
Use None to just show the boundary of the region:
TextureCoordinateFunction (4)
Applications (25)
Basic Shapes (5)
Advanced Shapes (2)
Mathematical Identities (1)
Regions of Convergence (6)
Plot the region of convergence for a geometric series:
Plot the region of convergence for a Laurent series:
Plot the region of convergence for an infinite series:
Plot the intervals of convergence of related power series:
Infinite sums of the summands can all be analytically continued to the entire complex plane as ![]() for all
for all ![]() :
:
Mapping Complex Regions (7)
Define an additive function ![]() that shifts a region in the
that shifts a region in the ![]() plane by an amount
plane by an amount ![]() to a region in the
to a region in the ![]() plane with the same size, shape and orientation:
plane with the same size, shape and orientation:
Specify a rectangle in the ![]() plane:
plane:
You can find an algebraic representation of the region in the ![]() plane by applying rect to
plane by applying rect to ![]() :
:
Plot the rectangles in the ![]() and
and ![]() planes:
planes:
If you plot rect[f[z]], then you get the pre-image of rect[z]:
Plot the disks in the ![]() and
and ![]() planes:
planes:
Define a linear function ![]() that scales and rotates a region in the
that scales and rotates a region in the ![]() plane to a region in the
plane to a region in the ![]() plane with the same shape:
plane with the same shape:
Specify a rectangle in the ![]() plane:
plane:
Plot the rectangles in the ![]() and
and ![]() planes:
planes:
The scaling factor from the ![]() plane to the
plane to the ![]() plane is Abs[c] and the angle of rotation is Arg[c]:
plane is Abs[c] and the angle of rotation is Arg[c]:
Plot the disks in the ![]() and
and ![]() planes:
planes:
Define an affine function that combines scaling by Abs[c], rotation by Arg[c] and a shift of ![]() :
:
Specify a rectangle in the ![]() plane:
plane:
Plot the rectangles in the ![]() and
and ![]() planes:
planes:
Plot the disks in the ![]() and
and ![]() planes:
planes:
The reciprocal function maps the interior of a circle centered at ![]() to its exterior:
to its exterior:
Specify a square in the ![]() plane:
plane:
Plot the square in the ![]() plane and its image in the
plane and its image in the ![]() plane:
plane:
To determine the shape of the boundary in the ![]() plane, consider the top edge of the square in the
plane, consider the top edge of the square in the ![]() plane where
plane where ![]() ,
, ![]() , and show that corresponds to a half-circle in the
, and show that corresponds to a half-circle in the ![]() plane centered at
plane centered at ![]() with radius
with radius ![]() :
:
Alternatively, you can algebraically describe the transformed region:
Separating the compound inequality into its two components illustrates the four bounding semicircles:
Linear fractional transformations famously map circles and lines to circles and lines. This linear fractional transformation maps the upper half-plane to the unit disk:
Define a function specifying the upper half-plane:
Plot the upper half of the ![]() plane and its image in the
plane and its image in the ![]() plane:
plane:
See that the unit disk is mapped to the right half-plane:
Define a function specifying the right half-plane:
Observe that the right half-plane is mapped to the upper half-plane:
This suggests that ![]() , and you can confirm that with NestList:
, and you can confirm that with NestList:
This boundary of the rectangle is composed of lines, and the boundary of its image consists of circles:
Define an exponential function:
Define a rectangle in the ![]() plane:
plane:
The rectangle in the ![]() plane is mapped to a sector of a disk in the
plane is mapped to a sector of a disk in the ![]() plane:
plane:
Define the unit disk in the ![]() plane:
plane:
The disk in the ![]() plane is mapped to a another disk in the
plane is mapped to a another disk in the ![]() plane:
plane:
Define a logarithmic function:
You can explicitly compute the inverse of f:
The annulus is mapped to the exterior of an ellipse within a horizontal strip:
Physics Applications (1)
Other Applications (3)
Plot regions for contour integrals:
Integrating ![]() around the boundary of
around the boundary of ![]() and taking
and taking ![]() and
and ![]() can be used to evaluate the following integral:
can be used to evaluate the following integral:
A function of a complex variable ![]() can have different asymptotic expansions depending on Arg[z]. The boundary between regions is called an (anti-)Stokes line. For example, the complex function
can have different asymptotic expansions depending on Arg[z]. The boundary between regions is called an (anti-)Stokes line. For example, the complex function ![]() is asymptotically equivalent to
is asymptotically equivalent to ![]() , so you can regard the imaginary axis as an (anti-)Stokes line:
, so you can regard the imaginary axis as an (anti-)Stokes line:
Consider a different complex function:
Note that the series expansion has a complicated dependence on Arg[z]:
Plot the regions where the three different asymptotic expansions hold:
Properties & Relations (8)
ComplexRegionPlot is a special case of RegionPlot:
ComplexContourPlot plots curves over the complexes:
ComplexPlot shows the argument and magnitude of a function using color:
Use ComplexPlot3D to use the ![]() axis for the magnitude:
axis for the magnitude:
Use ComplexArrayPlot for arrays of complex numbers:
Use ReImPlot and AbsArgPlot to plot complex values over the real numbers:
Use ComplexListPlot to show the location of complex numbers in the plane:
ComplexStreamPlot and ComplexVectorPlot treat complex numbers as directions:
Possible Issues (1)
RegionPlot will only visualize two-dimensional regions:
Related Guides
History
Text
Wolfram Research (2020), ComplexRegionPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
CMS
Wolfram Language. 2020. "ComplexRegionPlot." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ComplexRegionPlot.html.
APA
Wolfram Language. (2020). ComplexRegionPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ComplexRegionPlot.html
BibTeX
@misc{reference.wolfram_2025_complexregionplot, author="Wolfram Research", title="{ComplexRegionPlot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ComplexRegionPlot.html}", note=[Accessed: 23-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_complexregionplot, organization={Wolfram Research}, title={ComplexRegionPlot}, year={2020}, url={https://reference.wolfram.com/language/ref/ComplexRegionPlot.html}, note=[Accessed: 23-February-2026]}