ComplexListPlot[{z1,z2,…}]
plots complex numbers z1, z2, … as points in the complex plane.
ComplexListPlot[{data1,data2,…}]
plots data from all datai.
ComplexListPlot[{…,w[datai,…],…}]
plots ![]() with features defined by the symbolic wrapper w.
with features defined by the symbolic wrapper w.




ComplexListPlot
ComplexListPlot[{z1,z2,…}]
plots complex numbers z1, z2, … as points in the complex plane.
ComplexListPlot[{data1,data2,…}]
plots data from all datai.
ComplexListPlot[{…,w[datai,…],…}]
plots ![]() with features defined by the symbolic wrapper w.
with features defined by the symbolic wrapper w.
Details and Options




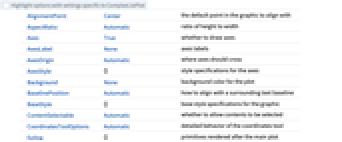
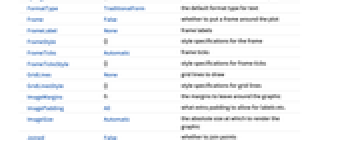
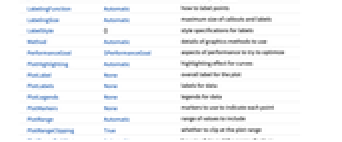
- The datai have the following forms and interpretations:
-
<|"k1"z1,"k2"z2,…|> values {z1,z2,…} {z1"lbl1",z2"lbl2",…}, {z1,z2,…}{"lbl1","lbl2",…} values {z1,z2,…} with labels {lbl1,lbl2,…} SparseArray values as a normal array - ComplexListPlot[Tabular[…]cspec] extracts and plots values from the tabular object using the column specification cspec.
- The following forms of column specifications cspec are allowed for plotting tabular data:
-
col plot complex values from column col {col1,col2,…} plot values from columns col1, col2, … - The following wrappers w can be used for the datai:
-
Annotation[datai,label] provide an annotation for the data Button[datai,action] define an action to execute when the data is clicked Callout[datai,label] label the data with a callout Callout[datai,label,pos] place the callout at relative position pos EventHandler[datai,…] define a general event handler for the data Highlighted[datai,effect] dynamically highlight fi with an effect Highlighted[datai,Placed[effect,pos]] statically highlight fi with an effect at position pos Hyperlink[datai,uri] make the data a hyperlink Labeled[datai,label] label the data Labeled[datai,label,pos] place the label at relative position pos Legended[datai,label] identify the data in a legend PopupWindow[datai,cont] attach a popup window to the data StatusArea[datai,label] display in the status area on mouseover Style[datai,styles] show the data using the specified styles Tooltip[datai,label] attach a tooltip to the data Tooltip[datai] use data values as tooltips - Wrappers w can be applied at multiple levels:
-
{…,w[zi],…} wrap the value zi in data w[datai] wrap the data w[{data1,…}] wrap a collection of datai w1[w2[…]] use nested wrappers - Callout, Labeled and Placed can use the following positions pos:
-
Automatic automatically placed labels Above, Below, Before, After positions around the data x near the data at a position x Scaled[s] scaled position s along the data {s,Above},{s,Below},… relative position at position s along the data {pos,epos} epos in label placed at relative position pos of the data - ComplexListPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
Axes True whether to draw axes Joined False whether to join points LabelingFunction Automatic how to label points LabelingSize Automatic maximum size of callouts and labels PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for curves PlotLabel None overall label for the plot PlotLabels None labels for data PlotLegends None legends for data PlotMarkers None markers to use to indicate each point PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotStyle Automatic graphics directives to determine styles of points PlotTheme $PlotTheme overall theme for the plot PolarAxes False whether to draw polar axes PolarAxesOrigin Automatic where to draw polar axes PolarGridLines None polar gridlines to draw PolarTicks Automatic polar axes ticks ScalingFunctions None how to scale individual coordinates - LabelingFunction->f specifies that each point should have a label given by f[value,index,lbls], where value is the value associated with the point, index is its position in the data and lbls is the list of relevant labels.
- Typical settings for PlotLegends include:
-
None no legend Automatic automatically determine legend {lbl1,lbl2,…} use lbl1, lbl2, … as legend labels Placed[lspec,…] specify placement for legend - ColorData["DefaultPlotColors"] gives the default sequence of colors used by PlotStyle.
- The arguments supplied to functions in MeshFunctionsare x, y, θ, r where θ and r are the argument and radius of the zi. Functions in ColorFunction are by default supplied with scaled versions of these arguments.
- Possible highlighting effects for Highlighted and PlotHighlighting include:
-
style highlight the indicated data 
"Ball" highlight and label the indicated point in data 
"Dropline" highlight and label the indicated point in data with droplines to the axes 
"XSlice" highlight and label all points along a vertical slice 
"YSlice" highlight and label all points along a horizontal slice 
Placed[effect,pos] statically highlight the given position pos - Highlight position specifications pos include:
-
x, {x} effect at {x,y}, with y chosen automatically {x,y} effect at {x,y} {pos1,pos2,…} multiple positions posi - ScalingFunctions->"scale" scales the modulus of the zi. ScalingFunctions{"scalex","scaley"} scales the
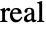 and imaginary components, respectively.
and imaginary components, respectively. -
 Highlight options with settings specific to ComplexListPlot
Highlight options with settings specific to ComplexListPlot
-
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes True whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic Joined False whether to join points LabelingFunction Automatic how to label points LabelingSize Automatic maximum size of callouts and labels LabelStyle {} style specifications for labels Method Automatic details of graphics methods to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for curves PlotLabel None overall label for the plot PlotLabels None labels for data PlotLegends None legends for data PlotMarkers None markers to use to indicate each point PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to determine styles of points PlotTheme $PlotTheme overall theme for the plot PolarAxes False whether to draw polar axes PolarAxesOrigin Automatic where to draw polar axes PolarGridLines None polar gridlines to draw PolarTicks Automatic polar axes ticks PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame ScalingFunctions None how to scale individual coordinates Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks
List of all options
Examples
open all close allBasic Examples (4)
Scope (39)
Data (7)
A list of complex values ![]() is plotted as a list of
is plotted as a list of ![]() pairs:
pairs:
Plot multiple sets of regular data:
Non-numeric and missing data is excluded:
Use MaxPlotPoints to limit the number of points used:
PlotRange is selected automatically:
Use PlotRange to focus on areas of interest:
Use ScalingFunctions to scale the axes:
Tabular Data (1)
Get tabular data of the results of running Newton's method to solve ![]() with random starting seeds:
with random starting seeds:
Plot all the points in the table:
Use PivotToColumns to generate columns for each basin of attraction:
Special Data (4)
Specify strings to use as labels:
Specify a location for labels:
Numeric values in an Association are used as the ![]() coordinates:
coordinates:
Plot data in a SparseArray:
Wrappers (6)
Use wrappers on individual data, datasets or collections of datasets:
Use a specific label for all of the points:
Label points with automatically positioned text:
Use PopupWindow to click an eigenvalue to see a corresponding eigenvector:
Button can be used to trigger any action:
Labeling and Legending (15)
Label points with automatically positioned text:
Place the labels relative to the points:
Label data with Labeled:
Label data with PlotLabels:
Place the label near the points at a particular ![]() value:
value:
Specify the text position relative to the point:
Label data automatically with Callout:
Place a label with a specific location:
Specify label names with LabelingFunction:
For dense sets of points, some labels may be turned into tooltips by default:
Increasing the size of the plot will show more labels:
Include legends for each datai:
Use Legended to provide a legend for a specific dataset:
Use Placed to change the legend location:
Use association keys as labels:
Plots usually have interactive callouts showing the coordinates when you mouse over them:
Presentation (6)
Multiple datasets are automatically colored to be distinct:
Provide explicit styling to different sets:
Include legends for each dataset:
Use Legended to provide a legend for a specific dataset:
Provide an interactive Tooltip for the data:
Use shapes to distinguish different datasets:
Use labels to distinguish different datasets:
Use Joined to connect datasets with lines:
Use InterpolationOrder to smooth joined data:
Options (156)
AspectRatio (4)
By default, the ratio of the height to width for the plot is determined automatically:
Use numerical value to specify the height to width ratio:
Make the height the same as the width with AspectRatio1:
AspectRatioFull adjusts the height and width to tightly fit inside other constructs:
Axes (3)
By default, ComplexListPlot draws axes:
Use AxesOrigin to specify where the axes intersect:
AxesOrigin (2)
AxesStyle (4)
ClippingStyle (4)
ClippingStyle requires at least one dataset to be Joined:
Omit clipped regions of the plot:
Show clipped regions as red at the bottom and thick at the top:
ColorFunction (3)
Color by scaled ![]() ,
, ![]() ,
, ![]() and
and ![]() coordinates:
coordinates:
ColorFunction has higher priority than PlotStyle for coloring the curve:
Use Automatic in MeshShading to use ColorFunction:
ColorFunctionScaling (4)
ColorFunctionScaling requires at least one dataset to be Joined:
Color the curve based on the scaled ![]() value:
value:
Frame (3)
FrameLabel (4)
FrameTicks (9)
Frame ticks are placed automatically by default:
Use frame ticks on the bottom edge:
By default, the top and right edges have tick marks but no tick labels:
Use All to include tick labels on all edges:
Place tick marks at specific positions:
Draw frame tick marks at specified positions with specific labels:
Specify the lengths for tick marks as a fraction of the graphics size:
Use different sizes in the positive and negative directions for each tick mark:
Specify a style for each frame tick:
Construct a function that places frame ticks at the midpoint and extremes of the frame edge:
FrameTicksStyle (3)
ImageSize (8)
Use named sizes such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
The number of points that are labeled directly may depend on the image size:
InterpolationOrder (4)
InterpolationOrder requires at least one dataset to be Joined:
By default, linear interpolation is used:
Joined (3)
LabelingFunction (7)
A Rule can be used to label points if the lists of values and labels are the same length:
A list of rules and values can be used to label selected points:
Use LabelingFunctionNone to suppress the labels:
Put the labels above the points:
Put them in a Tooltip:
LabelingSize (3)
MaxPlotPoints (1)
Use MaxPlotPoints to limit the number of points used:
Mesh (6)
MeshFunctions (3)
MeshFunctions requires at least one dataset to be Joined:
Show 5 mesh levels in the ![]() direction (red) and 10 in the
direction (red) and 10 in the ![]() direction (blue):
direction (blue):
MeshShading (7)
MeshShading requires at least one dataset to be Joined:
Alternate red and blue segments of equal width in the ![]() direction:
direction:
Use None to remove segments:
MeshShading can be used with PlotStyle:
MeshShading has higher priority than PlotStyle:
Use PlotStyle for some segments by setting MeshShading to Automatic:
MeshShading can be used with ColorFunction:
PlotHighlighting (7)
Plots have interactive coordinate callouts with the default setting PlotHighlightingAutomatic:
Use PlotHighlightingNone to disable the highlighting for the entire plot:
Use Highlighted[…,None] to disable highlighting for a single set:
Move the mouse over a set of points to highlight it using arbitrary graphics directives:
Move the mouse over the points to highlight them with balls and labels:
Move the mouse over the curve to highlight it with a label and droplines to the axes:
Use a component that shows the points on the plot closest to the ![]() position of the mouse cursor:
position of the mouse cursor:
Specify the style for the points:
Use a component that shows the coordinates on the points closest to the mouse cursor:
Use Callout options to change the appearance of the label:
PlotLabels (5)
Specify text to label sets of points:
Place the labels above the points:
Use callouts to identify the points:
Use the keys from an Association as labels:
Use None to not add a label:
PlotLegends (6)
Generate a legend using labels:
Generate a legend using placeholders:
Legends use the same styles as the plot:
Use Placed to specify the legend placement:
Place the legend inside the plot:
Use PlotLegends to change the appearance:
PlotMarkers (8)
ComplexListPlot normally uses distinct colors to distinguish different sets of data:
Automatically use colors and shapes to distinguish sets of data:
Change the size of the default plot markers:
Use arbitrary text for plot markers:
Use explicit graphics for plot markers:
PlotRange (4)
PlotRange is automatically calculated:
Explicitly choose the ![]() and
and ![]() ranges:
ranges:
Implicitly choose the ![]() and
and ![]() ranges by giving complex coordinates of the bottom-left and top-right corners:
ranges by giving complex coordinates of the bottom-left and top-right corners:
PlotStyle (7)
Use different style directives:
By default, different styles are chosen for multiple datasets:
Explicitly specify the style for different datasets:
PlotStyle applies to both curves and points:
PlotStyle can be combined with ColorFunction:
PlotStyle can be combined with MeshShading:
PlotTheme (2)
PolarAxesOrigin (2)
PolarGridLines (2)
PolarTicks (4)
ScalingFunctions (3)
A single scaling function scales the data radially:
Specifying two scaling functions scales the data in the ![]() and
and ![]() directions separately:
directions separately:
None indicates no scaling in the specified direction:
Ticks (9)
Ticks are placed automatically for each axis:
Use TicksNone to draw axes without any tick marks:
Use ticks on the ![]() axis, but not the imaginary axis:
axis, but not the imaginary axis:
Place tick marks at specific positions:
Draw tick marks at the specified positions with specific labels:
Use specific ticks on one axis and automatic ticks on the other:
Specify the lengths for ticks as a fraction of graphics size:
Use different sizes in the positive and negative directions for each tick:
Specify a style for each tick:
Construct a function that places ticks at the midpoint and extremes of the axis:
Applications (9)
Plot a discrete time signal and its spectrum:
Graph zeros of the zeta function:
Graph eigenvalues of a Cauchy matrix:
Show Gershgorin discs and eigenvalues for a matrix:
Show the eigenvalues for a PDE problem. Seek solutions of the structurally damped wave equation ![]() ,
, ![]() of the form
of the form ![]() :
:
Visualize iterations of Newton's method:
The eigenvalues of bipartite graphs are symmetric about the imaginary axis:
Properties & Relations (9)
Use ListPlot, ListLinePlot or ListPolarPlot for real data:
ComplexListPlot is closely related to ListPlot:
Use ComplexPlot to use color to show the argument and magnitude of a function:
Use ComplexPlot3D to use the ![]() axis for the magnitude:
axis for the magnitude:
Use ComplexArrayPlot for arrays of complex numbers:
Use ReImPlot and AbsArgPlot to plot complex values over the real numbers:
ComplexContourPlot plots curves over the complexes:
ComplexRegionPlot plots regions over the complexes:
ComplexStreamPlot and ComplexVectorPlot treat complex numbers as directions:
Possible Issues (2)
Neat Examples (3)
Eigenvalue analysis of the weighted adjacency matrix of the wins by teams in the National Hockey League in the 2010–2011 regular season:
Symmetry in the real parts of the eigenvalues of an adjacency matrix for a graph suggests that the graph may be bipartite, but in this case the graph is not bipartite:
Compute an integer two times the numbers in {0,1,…,n-1} modulo ![]() :
:
Graphically represent the integer ![]() as the point
as the point ![]() in the complex plane and connect the dots between the points representing
in the complex plane and connect the dots between the points representing ![]() and
and ![]() :
:
Related Guides
Text
Wolfram Research (2019), ComplexListPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/ComplexListPlot.html (updated 2025).
CMS
Wolfram Language. 2019. "ComplexListPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/ComplexListPlot.html.
APA
Wolfram Language. (2019). ComplexListPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ComplexListPlot.html
BibTeX
@misc{reference.wolfram_2025_complexlistplot, author="Wolfram Research", title="{ComplexListPlot}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/ComplexListPlot.html}", note=[Accessed: 21-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_complexlistplot, organization={Wolfram Research}, title={ComplexListPlot}, year={2025}, url={https://reference.wolfram.com/language/ref/ComplexListPlot.html}, note=[Accessed: 21-December-2025]}