DiagonalMatrix[list]
gives a matrix with the elements of list on the leading diagonal, and zero elsewhere.
DiagonalMatrix[list,k]
gives a matrix with the elements of list on the k![]() diagonal.
diagonal.
DiagonalMatrix[list,k,n]
pads with zeros to create an n×n matrix.


DiagonalMatrix
DiagonalMatrix[list]
gives a matrix with the elements of list on the leading diagonal, and zero elsewhere.
DiagonalMatrix[list,k]
gives a matrix with the elements of list on the k![]() diagonal.
diagonal.
DiagonalMatrix[list,k,n]
pads with zeros to create an n×n matrix.
Details and Options



- A diagonal matrix can be used to scale the rows of a matrix by multiplying from the left, or scale the columns by multiplying from the right.
- In the diagonal matrix given by DiagonalMatrix[{d1,…,dn}], the entries are given by
![D〚i,j〛=d_iTemplateBox[{{i, ,, j}}, KroneckerDeltaSeq] D〚i,j〛=d_iTemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]](Files/DiagonalMatrix.en/3.png) ; that is,
; that is, 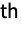 for the i
for the i leading diagonal entry and 0 otherwise.
leading diagonal entry and 0 otherwise. - DiagonalMatrix[list] is a symmetric matrix, and is thus equal to its transpose.
- For positive k, DiagonalMatrix[{d1,…,ds},k] puts the elements k positions above the leading diagonal, while DiagonalMatrix[{d1,…,ds},-k] puts the elements k positions below the leading diagonal of a matrix of size
![(TemplateBox[{k}, Abs]+s)x(TemplateBox[{k}, Abs]+s) (TemplateBox[{k}, Abs]+s)x(TemplateBox[{k}, Abs]+s)](Files/DiagonalMatrix.en/7.png) . Different values of k lead to different matrix dimensions.
. Different values of k lead to different matrix dimensions. - DiagonalMatrix[list] is equivalent to DiagonalMatrix[list,0].
- DiagonalMatrix[list,k,n] always creates an n×n matrix, even if this requires dropping elements of list. »
- The determinant of a diagonal matrix is the product of the leading diagonal entries if
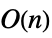 , and 0 otherwise.
, and 0 otherwise. - DiagonalMatrix[list,k,{m,n}] creates an m×n matrix.
- DiagonalMatrix[SparseArray[…],…] gives a SparseArray object.
- DiagonalMatrix[…,TargetStructure->struct] returns the diagonal matrix in the format specified by struct. Possible settings include:
-
Automatic automatically choose the representation returned "Dense" represent the matrix as a dense matrix "Sparse" represent the matrix as a sparse array "Structured" represent the matrix as a structured array "Symmetric" represent the matrix as a symmetric matrix - With DiagonalMatrix[…,TargetStructureAutomatic], a dense matrix is returned if the number of matrix entries is less than a preset threshold, and a structured array is returned otherwise.
- Diagonal matrices, when represented as structured arrays, allow for efficient storage and more efficient operations, including Det, Inverse and LinearSolve.
- Operations that are accelerated for DiagonalMatrix include:
-
Det time 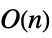
Dot time 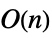
Inverse time 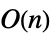
LinearSolve time 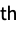
- For a structured DiagonalMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
-
"Diagonal" list of entries on the k  diagonal
diagonal"Offset" the offset k "Properties" list of supported properties "Structure" type of structured array "StructuredData" internal data stored by the structured array "StructuredAlgorithms" list of functions with special methods for the structured array "Summary" summary information, represented as a Dataset - Normal[DiagonalMatrix[…]] gives the diagonal matrix as an ordinary matrix.
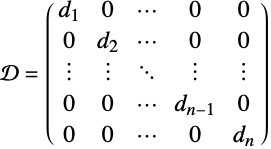
Examples
open all close allScope (6)
The elements in DiagonalMatrix are chosen to match the elements of the vector:
Arbitrary-precision number entries:
Pad with zeros to make a larger square matrix:
Make a square matrix with the specified dimension:
Rectangular diagonal matrices:
Construct a sparse diagonal matrix using the option setting TargetStructure"Sparse":
The sparse representation saves a significant amount of memory for larger matrices:
Generate a structured diagonal matrix using the option setting TargetStructure"Structured":
The representation and computation are efficient for the structured array:
The normal representation is dramatically bigger and slower:
The inverse needs a large amount of storage:
DiagonalMatrix objects include properties that give information about the array:
"Diagonal" gives the diagonal entries:
"Offset" gives the offset, which is zero, positive or negative if the diagonal elements are respectively on, above or below the main diagonal:
The "Summary" property gives a brief summary of information about the array:
The "StructuredAlgorithms" property lists the functions that have structured algorithms:
Options (3)
TargetStructure (3)
Return the diagonal matrix as a dense matrix:
Return the diagonal matrix as a structured array:
Return the diagonal matrix as a sparse array:
With the setting TargetStructureAutomatic, a dense matrix is returned for small dimensions:
For large dimensions, a structured representation is returned:
The dense representation uses a lot of memory for large lists:
Applications (5)
Express a matrix as the sum of its diagonal and off-diagonal parts:
Verify the similarity of a matrix to the diagonal matrix of its eigenvalues:
Construct a 5×5 tridiagonal matrix:
This can also be done using Band:
Properties & Relations (9)
IdentityMatrix is a special case of DiagonalMatrix:
Convert IdentityMatrix to a structured DiagonalMatrix:
DiagonalMatrix creates matrices that are DiagonalMatrixQ:
DiagonalMatrix[l] is UpperTriangularMatrixQ and LowerTriangularMatrixQ:
Several simple properties hold for diagonal matrices:
Inverse, MatrixExp and MatrixPower commute with DiagonalMatrix:
Det and Tr have commuting relations:
The permanent of the product of a diagonal matrix and a general matrix is equal to the permanent of the general matrix multiplied by the diagonal elements of the diagonal matrix:
Diagonal of DiagonalMatrix gives the original vector:
This is true even if the vector is a SparseArray object:
Matrices with only subdiagonals or superdiagonals are always nilpotent:
The size of the matrix generated by DiagonalMatrix[list,k] equals Length[list]+Abs[k]:
Band can be used to construct diagonals equivalent to DiagonalMatrix[list,k]:
They will be SameQ with the setting TargetStructure"Sparse":
See Also
DiagonalMatrixQ IdentityMatrix Diagonal Tr KroneckerDelta Band SparseArray
Function Repository: BlockDiagonalMatrix AntidiagonalMatrix
Tech Notes
History
Introduced in 1988 (1.0) | Updated in 2007 (6.0) ▪ 2008 (7.0) ▪ 2023 (13.3) ▪ 2024 (14.0)
Text
Wolfram Research (1988), DiagonalMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/DiagonalMatrix.html (updated 2024).
CMS
Wolfram Language. 1988. "DiagonalMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/DiagonalMatrix.html.
APA
Wolfram Language. (1988). DiagonalMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiagonalMatrix.html
BibTeX
@misc{reference.wolfram_2025_diagonalmatrix, author="Wolfram Research", title="{DiagonalMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/DiagonalMatrix.html}", note=[Accessed: 28-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_diagonalmatrix, organization={Wolfram Research}, title={DiagonalMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/DiagonalMatrix.html}, note=[Accessed: 28-December-2025]}