DiagonalMatrix

DiagonalMatrix[list]

対角成分が list で与えられ，他の成分が0である行列を返す．

DiagonalMatrix[list,k]

k 次の対角上の list の要素の行列を返す．

DiagonalMatrix[list,k,n]

0で充填して n×n 行列を作る．

詳細とオプション

  • 対角行列を使って左から乗算することで行列の行をスケーリングしたり，右から乗算することで列をスケーリングしたりすることができる．
  • DiagonalMatrix[{d1,…,dn}]で与えられる対角行列 の成分は D〚i,j〛=d_iTemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]で与えられる．つまり，i 番目の主対角成分は 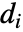でその他の成分は0である．
  • DiagonalMatrix[list]は対称行列である．したがってその転置に等しい．
  • k が正の場合，DiagonalMatrix[{d1,…,ds},k]は大きさが(TemplateBox[{k}, Abs]+s)x(TemplateBox[{k}, Abs]+s)の行列の成分を主対角の k 位置分上に，DiagonalMatrix[{d1,…,ds},-k]は，成分を主対角の k 位置分下に置く．k の値が異なると行列の大きさも異なる，
  • DiagonalMatrix[list]はDiagonalMatrix[list,0]に等しい．
  • DiagonalMatrix[list,k,n]は，たとえそのために list 中の要素を取り除くことが必要だとしても，常に n×n 行列を作る． »
  • 対角行列の行列式は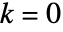，のときは主対角成分の積で，それ以外のときは0である．
  • DiagonalMatrix[list,k,{m,n}]は m×n 行列を作る．
  • DiagonalMatrix[SparseArray[…],…]はSparseArrayオブジェクトを返す．
  • DiagonalMatrix[…,TargetStructure->struct]は対角行列を struct で指定された形式で返す．次は，その可能な設定である．
  • Automatic返す際の表現を自動選択する
    "Dense"行列を密な行列として表す
    "Sparse"行列を疎な行列として表す
    "Structured"行列を構造化配列として表す
    "Symmetric"行列を対称行列として表す
  • DiagonalMatrix[…,TargetStructureAutomatic]の設定では，行列の成分数が設定された閾値未満の場合は密な行列が返され，それ以外の場合は構造化配列が返される．
  • 対角行列は，構造化配列として返される場合は，効率的な格納とDet，Inverse，LinearSolve等のより効率的な操作を可能にする．
  • 次は，DiagonalMatrixで加速される操作である．
  • Det時間
    Dot時間
    Inverse時間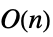
    LinearSolve時間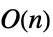
  • 構造化されたDiagonalMatrix sa は，次の特性"prop"に sa["prop"]でアクセスできる．
  • "Diagonal"k 番目の対角上の成分のリスト
    "Offset"オフセット k
    "Properties"サポートされる特性のリスト
    "Structure"構造化配列の型
    "StructuredData"構造化配列で保存されている内部データ
    "StructuredAlgorithms"構造化配列に対して特別なメソッドを持つ関数のリスト
    "Summary"Datasetして表される要約情報
  • Normal[DiagonalMatrix[…]]は対角行列を通常の行列として与える．

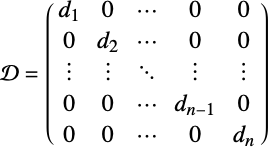
例題

すべて開くすべて閉じる

例  (1)

対角行列を構築する：

上対角行列：

下対角行列：

スコープ  (6)

DiagonalMatrix中の要素はベクトルの要素とマッチするように選ばれる：

厳密値の項目：

機械数の項目：

任意精度数の項目：

0で充填して大きい正方行列にする：

指定した大きさの正方行列を作る：

矩形対角行列：

オプション設定TargetStructure"Sparse"を使って疎な対角行列を構築する：

疎な表現を使うと大きい行列の場合はメモリが大幅に節約できる：

オプション設定TargetStructure"Structured"を使って構造化直交行列を構築する：

この表現と計算は構造化配列については効率的である：

通常の表現は非常に大きくなり計算も遅くなる：

逆行列には大きいストレージが必要である：

DiagonalMatrixオブジェクトは配列についての情報を与える特性を含む：

"Diagonal"は対角成分を与える：

"Offset"はオフセットを与える．これは，対角要素がそれぞれ主対角の上，その上，またはその下にある場合にそれぞれ0，正または負になる：

"Summary"特性は配列についての情報の簡単な要約を与える：

"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数のリストを与える：

オプション  (3)

TargetStructure  (3)

対角行列を密な行列として返す：

対角行列を構造化配列として返す：

対角行列を疎な配列として返す：

TargetStructureAutomaticの設定のとき，小さい次元では密な行列が返される：

次元が大きくなると構造化表現が返される：

密な表現は大きいリストの場合は大量のメモリを使う：

疎な表現が使うメモリは，通常は少ない：

構造化表現で使うメモリはさらに少なくなる：

アプリケーション  (5)

行列を対角部分とそれ以外の部分の和として表す：

行列とその固有値の対角行列の類似性を証明する：

ジョルダン(Jordan)行列を定義する：

5×5の3重対角行列を作る：

この行列はBandを使って作ることもできる：

対角矩形行列から対角成分を抽出する：

対角成分からもとの行列を再構築する：

特性と関係  (9)

IdentityMatrixはDiagonalMatrixの特殊ケースである：

IdentityMatrixを構造化DiagonalMatrixに変換する：

DiagonalMatrixはDiagonalMatrixQである行列を作る：

DiagonalMatrix[l]はUpperTriangularMatrixQおよびLowerTriangularMatrixQである：

いくつかの単純な特性は対角行列にも当てはまる：

Inverse，MatrixExp，MatrixPowerはDiagonalMatrixと交換できる：

DetとTrにも互換関係がある：

対角行列と一般行列の積の永久式は，一般行列に対角行列の対角成分を掛けたものの永久式に等しい：

DiagonalMatrixの対角(Diagonal)はもとのベクトルを返す：

これは，たとえベクトルがSparseArrayオブジェクトであってもそうである：

下対角あるいは上対角のみの行列は常にベキ零である：

DiagonalMatrix[list, k]で生成される行列のサイズはLength[list]+Abs[k]に等しい：

Bandを使ってDiagonalMatrix[list,k]と等価な対角が構築できる：

TargetStructure"Sparse"と設定すると両者はSameQになる：

Wolfram Research (1988), DiagonalMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiagonalMatrix.html （2024年に更新）.

テキスト

Wolfram Research (1988), DiagonalMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiagonalMatrix.html （2024年に更新）.

CMS

Wolfram Language. 1988. "DiagonalMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/DiagonalMatrix.html.

APA

Wolfram Language. (1988). DiagonalMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiagonalMatrix.html

BibTeX

@misc{reference.wolfram_2024_diagonalmatrix, author="Wolfram Research", title="{DiagonalMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/DiagonalMatrix.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_diagonalmatrix, organization={Wolfram Research}, title={DiagonalMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/DiagonalMatrix.html}, note=[Accessed: 17-November-2024 ]}