DiagonalMatrix
DiagonalMatrix[list]
给出主对角线元素为 list,其它元素为零的矩阵.
DiagonalMatrix[list,k]
给出第 k![]() 条对角线的元素为 list 的矩阵.
条对角线的元素为 list 的矩阵.
DiagonalMatrix[list,k,n]
与零合并创建一个 n×n 矩阵.
更多信息和选项



- 对角矩阵可以用来通过从左边的乘法来缩放矩阵的行,或者通过从右边的乘法来缩放列.
- 在 DiagonalMatrix[{d1,…,dn}] 给出的对角矩阵 中,项由
![D〚i,j〛=d_iTemplateBox[{{i, ,, j}}, KroneckerDeltaSeq] D〚i,j〛=d_iTemplateBox[{{i, ,, j}}, KroneckerDeltaSeq]](Files/DiagonalMatrix.zh/3.png) 给出,即
给出,即 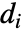 表示第 i
表示第 i 个先导对角项,且其他项为 0.
个先导对角项,且其他项为 0. - DiagonalMatrix[list] 是一个对称矩阵,因此等于其转置矩阵.
- 对于正值 k,DiagonalMatrix[{d1,…,ds},k] 将元素 k 位置置于先导对角项之上,而 DiagonalMatrix[{d1,…,ds},-k] 将元素 k 位置置于先导对角项之下,此时矩阵大小为
![(TemplateBox[{k}, Abs]+s)x(TemplateBox[{k}, Abs]+s) (TemplateBox[{k}, Abs]+s)x(TemplateBox[{k}, Abs]+s)](Files/DiagonalMatrix.zh/7.png) . k 的值不同会导致矩阵尺寸不同.
. k 的值不同会导致矩阵尺寸不同. - DiagonalMatrix[list] 等价于 DiagonalMatrix[list,0].
- DiagonalMatrix[list,k,n] 总是创建一个 n×n 矩阵,即使必须放弃 list 的元素. »
- 若
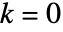 ,对角矩阵的行列式就是对角线先导项的乘积,否则为 0.
,对角矩阵的行列式就是对角线先导项的乘积,否则为 0. - DiagonalMatrix[list,k,{m,n}] 创建一个 m×n 矩阵.
- DiagonalMatrix[SparseArray[…],…] 给出一个 SparseArray 对象.
- DiagonalMatrix[…,TargetStructure->struct] 返回 struct 指定格式的对角矩阵. 可能设置包括:
-
Automatic 自动选择返回的表示 "Dense" 以稠密矩阵的形式表示矩阵 "Sparse" 以稀疏数组的形式表示矩阵 "Structured" 以结构化数组的形式表示矩阵 "Symmetric" 以对称矩阵的形式表示矩阵 - 设置 DiagonalMatrix[…,TargetStructureAutomatic],如果矩阵项数量小于预设阈值,则返回稠密矩阵,否则返回结构化数组.
- 对角矩阵在表示为结构化数组时,可以进行有效的存储和运算,包括 Det、Inverse 和 LinearSolve 的运算.
- 为 DiagonalMatrix 加速了的运算包括:
-
Det 时间 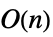
Dot 时间 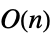
Inverse 时间 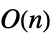
LinearSolve 时间 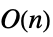
- 对于结构化的 DiagonalMatrix sa,下列属性 "prop" 可以 sa["prop"] 的形式访问:
-
"Diagonal" 第 k  条对角线上的项列表
条对角线上的项列表"Offset" 偏移量 k "Properties" 支持的属性列表 "Structure" 结构化数组的类型 "StructuredData" 结构化数组存储的内部数据 "StructuredAlgorithms" 为结构化数组提供特殊方法的函数列表 "Summary" 摘要信息,表示为 Dataset 的形式 - Normal[DiagonalMatrix[…]] 以普通矩阵的形式给出对角矩阵.
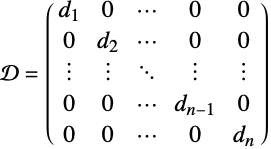
范例
打开所有单元关闭所有单元范围 (6)
DiagonalMatrix 中的元素匹配向量中的元素:
使用选项设置 TargetStructure"Sparse",可构建稀疏对角矩阵:
使用选项设置 TargetStructure"Structured",可生成结构化对角矩阵:
DiagonalMatrix 对象包括提供有关数组信息的属性:
选项 (3)
TargetStructure (3)
设置 TargetStructureAutomatic,在小型矩阵情况下会返回稠密矩阵:
应用 (5)
这也可以用 Band 实现:
属性和关系 (9)
IdentityMatrix 是 DiagonalMatrix 的一个特例:
将 IdentityMatrix 转换为结构化 DiagonalMatrix:
DiagonalMatrix 创建使 DiagonalMatrixQ 结果为真的矩阵:
DiagonalMatrix[l] 满足 UpperTriangularMatrixQ 和 LowerTriangularMatrixQ:
Inverse、MatrixExp 和 MatrixPower 与 DiagonalMatrix 的交换:
对角矩阵和一般矩阵的乘积的积和式等于一般矩阵的积和式乘以对角矩阵的对角线元素:
DiagonalMatrix 的 Diagonal 给出原始向量:
如果向量是一个 SparseArray 对象,则为 true:
DiagonalMatrix[list,k] 生成的矩阵大小等于 Length[list]+Abs[k]:
Band 可以用来构建等于 DiagonalMatrix[list,k] 的对角:
设置 TargetStructure"Sparse" 则其为 SameQ:
文本
Wolfram Research (1988),DiagonalMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiagonalMatrix.html (更新于 2024 年).
CMS
Wolfram 语言. 1988. "DiagonalMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/DiagonalMatrix.html.
APA
Wolfram 语言. (1988). DiagonalMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiagonalMatrix.html 年