DimensionReduction[{example1,example2,…}]
generates a DimensionReducerFunction[…] that projects from the space defined by the examplei to a lower-dimensional approximating manifold.
DimensionReduction[examples,n]
generates a DimensionReducerFunction[…] for an n-dimensional approximating manifold.
DimensionReduction[examples,n,props]
generates the specified properties of the dimensionality reduction.


DimensionReduction
DimensionReduction[{example1,example2,…}]
generates a DimensionReducerFunction[…] that projects from the space defined by the examplei to a lower-dimensional approximating manifold.
DimensionReduction[examples,n]
generates a DimensionReducerFunction[…] for an n-dimensional approximating manifold.
DimensionReduction[examples,n,props]
generates the specified properties of the dimensionality reduction.
Details and Options




- DimensionReduction can be used on many types of data, including numerical, textual, sounds, and images, as well as combinations of these.
- DimensionReduction[examples] yields a DimensionReducerFunction[…] that can be applied to data to perform dimension reduction.
- Each examplei can be a single data element, a list of data elements, an association of data elements, or a Dataset object.
- DimensionReduction[examples] automatically chooses an appropriate dimension for the target approximating manifold.
- DimensionReduction[examples] is equivalent to DimensionReduction[examples,Automatic].
- In DimensionReduction[…,props], props can be a single property or a list of properties. Possible properties include:
-
"ReducerFunction" DimensionReducerFunction[…] (default) "ReducedVectors" vectors obtained by reducing the examplei "ReconstructedData" reconstruction of examples after reduction and inversion "ImputedData" missing values in examples replaced by imputed values - The following options can be given:
-
FeatureExtractor Identity how to extract features from which to learn FeatureNames Automatic names to assign to elements of the examplei FeatureTypes Automatic feature types to assume for elements of the examplei Method Automatic which reduction algorithm to use PerformanceGoal Automatic aspect of performance to optimize RandomSeeding 1234 what seeding of pseudorandom generators should be done internally TargetDevice "CPU" the target device on which to perform training - Possible settings for PerformanceGoal include:
-
"Memory" minimize the storage requirements of the reducer function "Quality" maximize reduction quality "Speed" maximize reduction speed "TrainingSpeed" minimize the time spent producing the reducer - PerformanceGoal{goal1,goal2,…} will automatically combine goal1, goal2, etc.
- Possible settings for Method include:
-
Automatic automatically chosen method "Autoencoder" use a trainable autoencoder "Hadamard" project data using a Hadamard matrix "Isomap" isometric mapping "LatentSemanticAnalysis" latent semantic analysis method "Linear" automatically choose the best linear method "LLE" locally linear embedding "MultidimensionalScaling" metric multidimensional scaling "PrincipalComponentsAnalysis" principal components analysis method "TSNE" 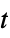 -distributed stochastic neighbor embedding algorithm
-distributed stochastic neighbor embedding algorithm"UMAP" uniform manifold approximation and projection - Possible settings for RandomSeeding include:
-
Automatic automatically reseed every time the function is called Inherited use externally seeded random numbers seed use an explicit integer or strings as a seed - DimensionReduction[…,FeatureExtractor"Minimal"] indicates that the internal preprocessing should be as simple as possible.
- DimensionReduction[DimensionReducerFunction[…],FeatureExtractorfe] can be used to prepend the FeatureExtractorFunction[…] fe to the existing feature extractor.
Examples
open all close allBasic Examples (3)
Generate a dimension reducer from a list of vectors:
Use this reducer on a new vector:
Use this reducer on a list of new vectors:
Create a reducer with a specified target dimension of 1:
Apply the reducer to the vectors used to generate the reducer:
Obtain both the reducer and the reduced vectors in one step:
Scope (7)
Create and visualize random 3D vectors:
Create a dimension reducer from the vectors:
Reduce the original vectors and visualize them:
Try to reconstruct the original vectors from the reduced ones:
The reconstructed vectors correspond to the original vectors projected on an approximating plane:
The reconstructed vectors can be directly obtained from the original vectors:
Generate a dimension reducer from a list of vectors:
Use the reducer function to impute missing values in other vectors:
Train a dimension reducer on a dataset of images:
Use the reducer on the training set:
Train a dimension reducer on textual data:
Use the reducer on new examples:
Train a dimension reducer on a list of DateObject:
Reduce the dimension of a new DateObject:
A string date can also be given:
Train a dimension reducer on a mixed-type dataset:
Reduce the dimension of a new example:
Options (7)
FeatureExtractor (1)
FeatureNames (1)
FeatureTypes (1)
Train a reducer on a simple dataset:
The first feature has been interpreted as numerical. Use FeatureTypes to enforce the interpretation of the first feature as nominal:
Method (3)
Generate a reducer function on the features of the Fisher iris dataset using the t-SNE method:
Group the examples by their species:
Reduce the dimension of the features:
Visualize the reduced dataset:
Perform the same operation using a different perplexity value:
Reduce the dimension of some images using the autoencoder method:
Visualize the two-dimensional representation of images:
Generate a nonlinear data manifold with the random noise, known as a Swiss-roll dataset:
Visualize the three-dimensional Swiss-roll dataset:
Train a reducer function using the isometric mapping (isomap) method:
Visualize the two-dimensional embedding of the reduced dataset:
Train a reducer function using the locally linear embedding (LLE) method:
Visualize the two-dimensional embedding of the reduced dataset:
TargetDevice (1)
Train a reducer function using a fully connected "AutoEncoder" on the system's default GPU and look at its AbsoluteTiming:
Compare the previous timing with the one obtained by using the default CPU computation:
Applications (5)
Dataset Visualization (1)
Load the Fisher iris dataset from ExampleData:
Generate a reducer function with the features of each example:
Group the examples by their species:
Head-Pose Estimation (1)
Generate a dataset of many heads with random view points, which creates different head poses:
Visualize different head poses:
Generate a reducer function on a dataset of images with different poses using the LLE method:
Visualize a two-dimensional representation of images from a 50×50 input space in which two axes represent up-down and front-side poses:
Image Imputation (1)
Load the MNIST dataset from ExampleData and keep the images:
Convert images to numerical data and separate the dataset into a training set and a test set:
The dimension of the dataset is 784:
Create a dimension reducer from the training set with a target dimension of 50:
Reduce a vector from the test set:
Visualize the original vector and its reconstructed version:
Replace some values of the vector by Missing[] and visualize it:
Impute missing values with the reducer function:
Visualize the original image, the image with missing values, and the imputed image:
Recommender System (1)
Get movie ratings of users in a SparseArray form:
The dataset is composed of 100 users and 10 movies. Ratings range from 1 to 5, and Missing[] represents unknown ratings:
Separate the dataset into a training set and a test set:
Generate a dimension reducer from the training set:
Use this dimension reducer to impute (that is, to predict) the missing values for a new user:
Image Search (1)
Construct a dataset of dog images:
Train a reducer function from this dataset:
Generate a NearestFunction in the reduced space:
Using the NearestFunction, construct a function that displays the nearest image of the dataset:
Use this function on images that are not in the dataset:
This reducer function can also be used to delete image pairs that are too similar:
Related Guides
History
Introduced in 2015 (10.1) | Updated in 2017 (11.1) ▪ 2017 (11.2) ▪ 2018 (11.3) ▪ 2020 (12.2)
Text
Wolfram Research (2015), DimensionReduction, Wolfram Language function, https://reference.wolfram.com/language/ref/DimensionReduction.html (updated 2020).
CMS
Wolfram Language. 2015. "DimensionReduction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/DimensionReduction.html.
APA
Wolfram Language. (2015). DimensionReduction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DimensionReduction.html
BibTeX
@misc{reference.wolfram_2025_dimensionreduction, author="Wolfram Research", title="{DimensionReduction}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DimensionReduction.html}", note=[Accessed: 15-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_dimensionreduction, organization={Wolfram Research}, title={DimensionReduction}, year={2020}, url={https://reference.wolfram.com/language/ref/DimensionReduction.html}, note=[Accessed: 15-February-2026]}