DiscreteUniformDistribution
DiscreteUniformDistribution[{imin,imax}]
iminから imaxまでの整数上での離散一様分布を表す.
DiscreteUniformDistribution[{{imin,imax},{jmin,jmax},…}]
{{imin,imax},{jmin,jmax},…}のボックス内の整数上の多変量離散一様分布を表す.
詳細
- DiscreteUniformDistributionは離散矩形分布としても知られている.
- 離散一様分布における値
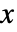 の確率は,
の確率は,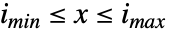 では整数
では整数 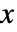 について一定であり,その他の場合は0である. »
について一定であり,その他の場合は0である. » - DiscreteUniformDistributionでは iminと imaxは imin<imaxである任意の整数でよい.
- DiscreteUniformDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- DiscreteUniformDistribution[{imin,imax}]は,確率変量が整数値
 のうちの任意の値を同じ確率で取る離散統計分布(離散矩形分布としても知られている)を表す.したがって,一様分布は完全にその領域の端点 iminおよび imaxによってパラメータ化され,その確率密度関数は区間
のうちの任意の値を同じ確率で取る離散統計分布(離散矩形分布としても知られている)を表す.したがって,一様分布は完全にその領域の端点 iminおよび imaxによってパラメータ化され,その確率密度関数は区間 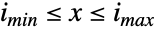 内の整数上では一定である.離散一様分布はUniformDistributionの離散バージョンであり,後者と同じように,離散一様分布もまた,ある領域上で確率が等しい複数の変量に一般化される.
内の整数上では一定である.離散一様分布はUniformDistributionの離散バージョンであり,後者と同じように,離散一様分布もまた,ある領域上で確率が等しい複数の変量に一般化される. - 公正なサイコロを振って任意の単一の値 k を得る尤度は,PDF[DiscreteUniformDistribution[{1,6}],k]で厳密にモデル化される.1つの正しいキーと n 個の不正なキーを含むキーホルダーがあるとして,値1,…,n に離散確率変量を使う逆変換メソッドの変形を使って正しいキーを見付けるまでの期待される不正なキーの選択回数をモデル化することができる.この問題は,いわゆる最大化問題の期待値と関連している.ドイツ戦車問題として知られるこの問題の例は,第二次世界大戦当時重要だったもので,DiscreteUniformDistribution[{1,N}]が,
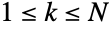 であるある整数 k について k 回の観察を与えるために必要な最大の
であるある整数 k について k 回の観察を与えるために必要な最大の 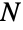 の予測を含んでいる.
の予測を含んでいる. - RandomVariateを使って,離散一様分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,DiscreteUniformDistribution[{imin,imax}]](より簡略すると xDiscreteUniformDistribution[{imin,imax}])を使って,確率変数 x が離散一様分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[DiscreteUniformDistribution[{imin,imax}],x]およびCDF[DiscreteUniformDistribution[{imin,imax}],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合が離散一様分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから離散パラメトリック一様分布を推定することが,FindDistributionParametersを使ってデータを離散一様分布にフィットすることができる.ProbabilityPlotを使って記号的離散一様分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号的離散一様分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された離散一様分布を表すことが,CopulaDistributionを使って離散一様分布を含む高次元分布を構築することが,ProductDistributionを使って離散一様分布を含む独立成分分布の結合分布を計算することができる.
- 離散一様分布は他の多くの分布に関連している.例えば,DiscreteUniformDistribution[{a,b}]は,a と b の両方が整数であるいという仮定のもとでの,UniformDistribution[{a,b}]の離散化バージョンである.DiscreteUniformDistributionは,離散一様分布に従って分布する,独立した n 個の確率変量
 の和
の和  (nPoissonDistribution)はそれ自身が変換されたポアソン分布であるという意味で,PoissonDistributionにも関連している.
(nPoissonDistribution)はそれ自身が変換されたポアソン分布であるという意味で,PoissonDistributionにも関連している.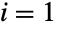 および2について(x1x1+x2)DiscreteUniformDistributionであるならxiGeometricDistributionであるという事実によって,離散一様分布はGeometricDistributionにも関連している.DiscreteUniformDistributionはまたBetaBinomialDistributionと,さらに接線方向にCompoundPoissonDistribution等の分布とも関連している.
および2について(x1x1+x2)DiscreteUniformDistributionであるならxiGeometricDistributionであるという事実によって,離散一様分布はGeometricDistributionにも関連している.DiscreteUniformDistributionはまたBetaBinomialDistributionと,さらに接線方向にCompoundPoissonDistribution等の分布とも関連している.
例題
すべて開くすべて閉じる例 (8)
スコープ (11)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無限に大きい区間での尖度はUniformDistributionの尖度に等しい:
アプリケーション (7)
DiscreteUniformDistributionの累積分布関数は右連続関数の例である:
0, 1, 2, 3と番号を付けられた4つのディスクを含むコンピュータがある.起動時に一時ファイルの保存用にディスクの1つが無作為に選ばれる.ディスク選択の確率を求める:
次の30回の起動時にどのディスクが選ばれるかのシミュレーションを行う:
公正な六面のサイコロはDiscreteUniformDistributionでモデル化することができる:
サイコロをランダムに振った場合を生成して確かめる.この場合は3個のサイコロを![]() 回振っている:
回振っている:
3個のサイコロの目のすべての可能性を明示的に列挙して確かめる:
2つの公正なサイコロを投げたとして,サイコロの値の差の分布を求める:
クラップスというゲームでは2個のサイコロが投げられる[MathWorld]:
2個のサイコロの目が両方とも1となる「ピンぞろ(snake eyes)」[MathWorld]の確率を求める:
「6ぞろ(boxcars)」[MathWorld]の確率:
合計が8になる「eighter from Decatur」[MathWorld]の確率:
合計が4になる「little Joe」[MathWorld]の確率:
1投で負けとなる,つまり,合計が2,3,12のいずれかになる確率を求める:
1投で勝ちとなる,つまり,合計が7か11になる確率を求める:
ある仮想のR&D企業では雇用者の少なくとも1人の誕生日である日が休日になるという.誕生日が独立分布に従うとして実働日数を最大にする雇用者数を求める:
ガリレオのサイコロ問題を解いて,3個のサイコロを振った場合に9が出る確率と10が出る確率を求める:
特性と関係 (3)
考えられる問題 (2)
テキスト
Wolfram Research (2007), DiscreteUniformDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html (2010年に更新).
CMS
Wolfram Language. 2007. "DiscreteUniformDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html.
APA
Wolfram Language. (2007). DiscreteUniformDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteUniformDistribution.html