gives the dual of the planar graph g.


DualPlanarGraph
gives the dual of the planar graph g.
Details and Options

- DualPlanarGraph is also known as geometric dual graph and combinatorial dual graph.
- DualPlanarGraph is typically used to associate dual structures such as flow and cellular networks, or Voronoi and Delaunay diagrams.
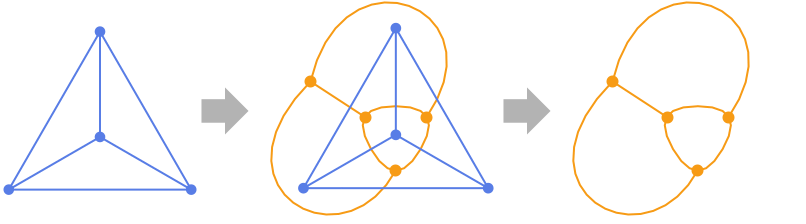
- DualPlanarGraph[g] gives a graph that has a vertex for each face of g and an edge for each pair of faces separated from each other by an edge.
- DualPlanarGraph takes the same options as Graph.
-
AlignmentPoint Center the default point in the graphic to align with AnnotationRules {} annotations for graph, edges and vertices AspectRatio Automatic ratio of height to width Axes False whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool DirectedEdges Automatic whether to interpret Rule as DirectedEdge EdgeLabels None labels and label placements for edges EdgeLabelStyle Automatic style to use for edge labels EdgeShapeFunction Automatic generate graphic shapes for edges EdgeStyle Automatic style used for edges EdgeWeight Automatic weights for edges Epilog {} primitives rendered after the main plot FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GraphHighlight {} graph elements to highlight GraphHighlightStyle Automatic style for highlight GraphLayout Automatic how to lay out vertices and edges GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels Method Automatic details of graphics methods to use PerformanceGoal Automatic aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotRange All range of values to include PlotRangeClipping False whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotTheme $PlotTheme overall theme for the graph PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks VertexCoordinates Automatic coordinates for vertices VertexLabels None labels and placements for vertices VertexLabelStyle Automatic style to use for vertex labels VertexShape Automatic graphic shape for vertices VertexShapeFunction Automatic generate graphic shapes for vertices VertexSize Medium size of vertices VertexStyle Automatic styles for vertices VertexWeight Automatic weights for vertices
List of all options


Examples
open all close allBasic Examples (2)
Scope (4)
Applications (1)
Properties & Relations (2)
Use PlanarFaceList to get the faces of planar graphs:
Use FindPlanarColoring to find a coloring for the faces of planar graphs:
Possible Issues (2)
DualPlanarGraph depends on faces based on the given layout:
DualPlanarGraph depends on faces based on the given coordinates:
Related Guides
History
Text
Wolfram Research (2021), DualPlanarGraph, Wolfram Language function, https://reference.wolfram.com/language/ref/DualPlanarGraph.html.
CMS
Wolfram Language. 2021. "DualPlanarGraph." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DualPlanarGraph.html.
APA
Wolfram Language. (2021). DualPlanarGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DualPlanarGraph.html
BibTeX
@misc{reference.wolfram_2025_dualplanargraph, author="Wolfram Research", title="{DualPlanarGraph}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/DualPlanarGraph.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_dualplanargraph, organization={Wolfram Research}, title={DualPlanarGraph}, year={2021}, url={https://reference.wolfram.com/language/ref/DualPlanarGraph.html}, note=[Accessed: 09-January-2026]}