Eigenvectors[m]
正方行列 m の固有ベクトルのリストを与える.
Eigenvectors[{m,a}]
a についての m の一般化された固有ベクトルを与える.
Eigenvectors[m,k]
m の最初の k 個の固有ベクトルを与える.
Eigenvectors[{m,a},k]
最初の k 個の一般化された固有ベクトルを与える.


Eigenvectors
Eigenvectors[m]
正方行列 m の固有ベクトルのリストを与える.
Eigenvectors[{m,a}]
a についての m の一般化された固有ベクトルを与える.
Eigenvectors[m,k]
m の最初の k 個の固有ベクトルを与える.
Eigenvectors[{m,a},k]
最初の k 個の一般化された固有ベクトルを与える.
詳細とオプション


- 行列 m が近似実数または近似複素数を含むとき,Eigenvectorsは固有ベクトルを数値で求める.
- 近似数値行列 m について,固有ベクトルは正規化される. »
- 厳密行列および記号行列 m については,固有ベクトルは正規化されない. »
- 縮退固有値に対する固有ベクトルは,線形独立となるよう選択される.
- nn 行列については,Eigenvectorsは,常に長さ n のリストを返す.このリストには,行列の独立した各固有ベクトルが含まれ,必要な場合には適切な数のゼロベクトルが補われる. »
- 数値的な固有値を持つ固有ベクトルは絶対値が大きいものから小さいものへの順に並べられる.
- 行列 m の固有ベクトルは,同じスカラー
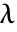 に対して
に対して 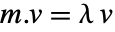 である非零の固有ベクトル
である非零の固有ベクトル 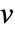 である. »
である. » - a についての m の一般化された固有ベクトルは
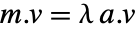 または
または 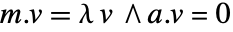 である
である 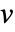 である. »
である. » - 行列 m と a が次元
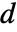 の零空間を共有するとき,それらの一般化された固有値の
の零空間を共有するとき,それらの一般化された固有値の 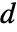 もまた零ベクトルとして返される. »
もまた零ベクトルとして返される. » - Eigenvectors[m,spec]はTake[Eigenvectors[m],spec]と等価である.
- Eigenvectors[m,UpTo[k]]は k 個(あるいはできるだけたくさん)の固有ベクトルを与える.
- EigenvectorsでSparseArrayオブジェクトと構造化配列を使うことができる.
- Eigenvectorsのオプションと設定値
-
Cubics False 三次方程式を解く際に累乗根を使うかどうか Method Automatic 使用するメソッド Quartics False 四次方程式を解く際に累乗根を使うかどうか ZeroTest Automatic 式が0ゼロのときに決定する検定 - ZeroTestオプションは,厳密行列および記号行列のみに使うことができる.
- 近似数値行列についての明示的なMethod設定
-
"Arnoldi" いくつかの固有値を求めるためのArnoldi反復法 "Banded" エルミート行列のための直接帯行列ソルバ "Direct" 全固有値を求めるための直接法 "FEAST" 区間内の固有値を求めるためのFEAST反復法(エルミート行列のみに適用可) - "Arnoldi"法は,対称行列あるいはエルミート行列に適用された際には,Lanczos法としても知られている.
- "Arnoldi"法および"FEAST"法はサブオプションMethod ->{"name",opt1->val1,…}を取る.これは,Methodのサブセクションで見ることができる.
例題
すべて開く すべて閉じる例 (5)
スコープ (20)
基本的な用法 (6)
固有ベクトルの部分集合 (5)
一般化された固有ベクトル (4)
特殊行列 (5)
QuantityArrayオブジェクトの単位は固有値に付き,固有ベクトルは無次元になる:
IdentityMatrix[n]の固有ベクトルはベクトル空間の標準バイアスを形成する:
HilbertMatrixの固有ベクトル:
行列を最初に数値化した場合,固有値は大きく変化しないが,固有ベクトルは著しく変化する:
これは,数値入力に対して固有ベクトルが正規化されるためである:
CenteredInterval行列の固有ベクトル:
オプション (10)
Cubics (1)
Method (8)
"Arnoldi" (5)
Arnoldi法は,機械精度および任意精度の行列に使うことができる.Arnoldi法の実装は,"ARPACK"ライブラリに基づいている.これは,大規模な疎配列に対して最も有効である.
"Arnoldi"法では,以下のサブオプションを指定することができる.
| "BasisSize" | Arnoldi基底の大きさ | |
| "Criteria" | 使用する基準 | |
| "MaxIterations" | 反復の最大数 | |
| "Shift" | Arnoldiシフト | |
| "StartingVector" | 反復を始める最初のベクトル | |
| "Tolerance" | 反復の終了に使用される許容度 |
| "Magnitude" | Absに基づく | |
| "RealPart" | Reに基づく | |
| "ImaginaryPart" | Imに基づく | |
| "BothEnds" | 実数値対称行列スペクトルの両端からのいくつかの固有値 |
さまざまな"Criteria"設定を使って最大固有値を計算する.行列 m は,固有値![]() を持つ:
を持つ:
デフォルトで,"Criteria"->"Magnitude"は最大規模の固有値に対応する固有ベクトルを選ぶ:
初期ベクトルが違うと収束する固有ベクトルも異なることがある:
"Shift"->μ を使い,行列 ![]() を
を ![]() に変換することで固有値をシフトさせる.これで固有ベクトルが保存されるが,固有値は-μ 変化する.このメソッドは,変化した固有値を相殺する."Shift"は,一般に,最大あるいは最小規模といった選択基準なしで固有ペアを求める際に使われる:
に変換することで固有値をシフトさせる.これで固有ベクトルが保存されるが,固有値は-μ 変化する.このメソッドは,変化した固有値を相殺する."Shift"は,一般に,最大あるいは最小規模といった選択基準なしで固有ペアを求める際に使われる:
"Banded" (1)
アプリケーション (16)
固有ベクトルの幾何学 (3)
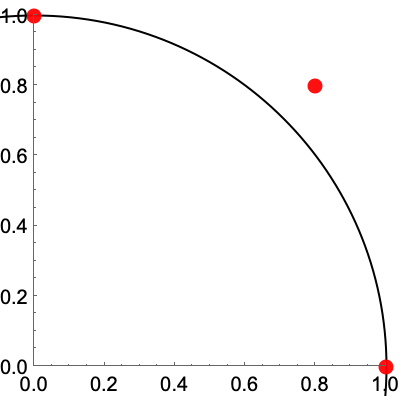
正の固有値を持つ固有ベクトルは,行列の作用を受けたときに同じ方向を指す:
負の固有値を持つ固有ベクトルは,行列の作用を受けたときに逆の方向を指す:
CoefficientArraysを使って二次形式の対称行列を得る:
対角化 (5)
これで,行列の任意の関数が ![]() として計算できるようになった.例えばMatrixPower:
として計算できるようになった.例えばMatrixPower:
同様に,MatrixExpが自明となって ![]() の対角要素を累乗することしか必要としなくなった:
の対角要素を累乗することしか必要としなくなった:
![]() を,その標準行列が行列
を,その標準行列が行列 ![]() で与えられる線形変換とする.基底
で与えられる線形変換とする.基底![]() における
における ![]() の表現が対角であるという特性を持つ
の表現が対角であるという特性を持つ![]() の基底
の基底 ![]() を求める:
を求める:
![]() が
が ![]() の固有ベクトルからなり,
の固有ベクトルからなり,![]() が列が
が列が ![]() の要素である行列であるとする:
の要素である行列であるとする:
![]() は
は ![]() の座標から標準座標に変換する.この逆変換は逆方向に変換する:
の座標から標準座標に変換する.この逆変換は逆方向に変換する:
実対称行列は,![]() のように直交対角化可能である.ただし,
のように直交対角化可能である.ただし,![]() は実対角行列であり
は実対角行列であり ![]() は直交行列である.次の行列が対象であることを確認し,次にこれを対角化する:
は直交行列である.次の行列が対象であることを確認し,次にこれを対角化する:
直交行列については,固有ベクトルを列に置く前にこれを正規化する必要がある:
![]() のとき,その行列は正規行列と呼ばれる.正規行列はユニタリ変換で対角化できる最も一般的な行列である.実対称行列
のとき,その行列は正規行列と呼ばれる.正規行列はユニタリ変換で対角化できる最も一般的な行列である.実対称行列 ![]() は,方程式の両辺が
は,方程式の両辺が ![]() なので,すべて正規行列である:
なので,すべて正規行列である:
NormalMatrixQを使って確認する:
固有ベクトルを正規化してこれを列に置くとユニタリ行列になる:
微分方程式と動的な系 (4)
常微分方程式の系 ![]() ,
, ![]() ,
, ![]() を解く.まず,右辺のために係数行列
を解く.まず,右辺のために係数行列 ![]() を構築する:
を構築する:
DSolveValueを使って解を確かめる:
粒子が平面の力場で動いており,その位置ベクトル ![]() が
が ![]() と
と ![]() を満足するとする.ただし,
を満足するとする.ただし,![]() と
と ![]() は以下であるとする.
は以下であるとする.![]() のときのこの初期値問題を解く:
のときのこの初期値問題を解く:
系の一般解は ![]() である.LinearSolveを使って係数を決定する:
である.LinearSolveを使って係数を決定する:
DSolveValueを使って解を確かめる:
固有値と固有ベクトルを求め,Chopを使って小さい数値誤差を切り捨てる:
物理 (4)
量子力学では,状態はエルミート線形演算子による複素単位ベクトルと物理量で表される.固有値は可能な観測値を表,固有ベクトルに関する成分の二乗係数をはそれらの観測値の確率を表す.与えられたスピン演算子 ![]() と状態
と状態 ![]() について,可能な観測値とその確率を求める:
について,可能な観測値とその確率を求める:
量子力学では,エネルギー演算子はハミルトニアン ![]() と呼ばれ,エネルギーが
と呼ばれ,エネルギーが ![]() の状態はシュレーディンガー方程式
の状態はシュレーディンガー方程式 ![]() に従って進化する.一定磁場で
に従って進化する.一定磁場で ![]() 方向にスピン1粒子に対するハミルトニアンが与えられたとして,初期状態が
方向にスピン1粒子に対するハミルトニアンが与えられたとして,初期状態が ![]() を表す状態
を表す状態![]() であった粒子の時点
であった粒子の時点 ![]() における状態を求める:
における状態を求める:
時点 ![]() における状態はシュレーディンガー方程式に従って進化する各固有状態の和である:
における状態はシュレーディンガー方程式に従って進化する各固有状態の和である:
慣性モーメントはさまざまな方向への回転に対する剛体の抵抗を表す実対称行列である.この行列の固有値は主慣性モーメントと呼ばれ,対応する固有ベクトル(必然的の直交ベクトル)は主軸である.以下の四面体の主慣性モーメントと主軸を求める:
一般化された固有系を使って項を分離するための練成振動の正規モードを求めることができる.以下の図に示した系について考える:
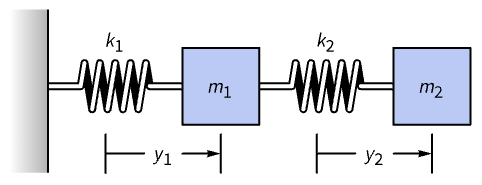
フックの法則によると,これは![]() と
と ![]() に従う.一般解の
に従う.一般解の ![]() を代入すると,以下のように,剛性行列
を代入すると,以下のように,剛性行列 ![]() ,質量行列
,質量行列 ![]() の行列方程式
の行列方程式 ![]() が与えられる:
が与えられる:
モードの形状は ![]() についての
についての ![]() の一般化された固有ベクトルから導かれる:
の一般化された固有ベクトルから導かれる:
特性と関係 (15)
厳密行列および記号行列に対して返される固有ベクトルは単位ベクトルではないことが多い:
Eigenvectors[m]は,事実上,Eigensystemが返す対の第2要素である:
固有ベクトルと固有値の両方が必要な場合は,Eigensystemを呼び出した方が効率的なことが多い:
固有ベクトルは![]() を解く.
を解く.![]() は固有多項式の根で
は固有多項式の根で ![]() は恒等行列である:
は恒等行列である:
CharacteristicPolynomialを使って根を求める:
等価性を確認するために,NullSpaceで求まった同次方程式の解を結合する:
一般化された固有ベクトルは,![]() を解く(ただし
を解く(ただし ![]() は一般化された固有多項式の根)かスカラー
は一般化された固有多項式の根)かスカラー ![]() について
について ![]() に従うかする:
に従うかする:
CharacteristicPolynomialを使うと根は1つしか求まらない:
行列 m はDiagonalizableMatrixQ[m]がTrueのときかつそのときに限って固有ベクトルの完全集合を持つ:
固有値は絶対値によってソートされるので,以下は同じベクトルを逆順で与える:
解析関数 ![]() について,
について,![]() の固有ベクトルは
の固有ベクトルは ![]() の固有ベクトルでもある:
の固有ベクトルでもある:
SingularValueDecomposition[m]は ![]() と
と![]() の固有ベクトルから構築される:
の固有ベクトルから構築される:
JordanDecomposition[m]は固有値と固有ベクトルから構築された行列![]() を返す:
を返す:
![]() 行列は列として,おそらくEigenvectorsからとは異なる順序の固有ベクトルを持つ:
行列は列として,おそらくEigenvectorsからとは異なる順序の固有ベクトルを持つ:
数値正規行列 ![]() のSchurDecomposition[n,RealBlockDiagonalFormFalse]:
のSchurDecomposition[n,RealBlockDiagonalFormFalse]:
行列 q はおそらくEigenvectorsからの順序とは異なる固有ベクトルで構築されている:
q が固有ベクトルを列として持つことを確認するために,各ベクトルの最初の項を1.に設定して q と v の位相差を消去する:
行列が次元 ![]() の零空間を共有するなら,Eigenvectors[m1,m2]は
の零空間を共有するなら,Eigenvectors[m1,m2]は ![]() 個の零ベクトルを持つ:
個の零ベクトルを持つ:
![]() のそれ自身についての一般化された固有値は2つの零ベクトルで充填される:
のそれ自身についての一般化された固有値は2つの零ベクトルで充填される:
考えられる問題 (5)
EigenvectorsとEigenvaluesは,対応する順序で結果を与える保証はない:
以下の特定の例では,7番目の固有ベクトルは7番目の固有値に対応しない:
Eigensystem[mat]を使って対応する結果が常に一致するようにする:
厳密計算にJordanDecompositionを使う:
数値計算にSchurDecompositionを使う:

最大固有値に対応するいくつかの固有ベクトルを計算する方がはるかに簡単である:
固有値が密接にグループ化されている場合は,疎行列に対する反復的な方法が収束しないことがある:

テクニカルノート
-
▪
- ベクトルと行列 ▪
- 固有値と固有ベクトル
関連するガイド
-
▪
- 行列の操作 ▪
- グラフプログラミング ▪
- 行列分解
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2003 (5.0) ▪ 2014 (10.0) ▪ 2015 (10.3) ▪ 2017 (11.1) ▪ 2024 (14.0)
テキスト
Wolfram Research (1988), Eigenvectors, Wolfram言語関数, https://reference.wolfram.com/language/ref/Eigenvectors.html (2024年に更新).
CMS
Wolfram Language. 1988. "Eigenvectors." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Eigenvectors.html.
APA
Wolfram Language. (1988). Eigenvectors. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Eigenvectors.html
BibTeX
@misc{reference.wolfram_2025_eigenvectors, author="Wolfram Research", title="{Eigenvectors}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Eigenvectors.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_eigenvectors, organization={Wolfram Research}, title={Eigenvectors}, year={2024}, url={https://reference.wolfram.com/language/ref/Eigenvectors.html}, note=[Accessed: 03-March-2026]}