FindSpanningTree
FindSpanningTree[{v1,v2,…,vn}]
viの間の総距離を最小にする全域木を求める.
頂点間の総距離を最小にするグラフ g の全域木を求める.
FindSpanningTree[{g,v},…]
頂点 v を含む g の連結成分の全域木を求める.
FindSpanningTree[{vw,…},…]
規則 vw を使ってグラフ g を指定する.
詳細とオプション


- FindSpanningTreeは最小全域木あるいは全域林としても知られている.
- 通常,閉路なしで最適な連結を見付けるために使用される.
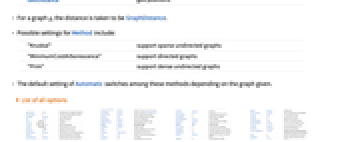
- FindSpanningTree[{v1,…,vn}]は,頂点が v1,…,vnの完全グラフにおける viの間の総距離を最小にする全域木を与える.
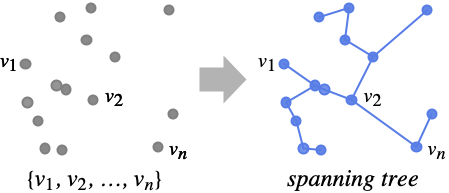
- 連結グラフ g の全域木は,木の形状をした g の部分グラフであり,g の全頂点を連結する.
- 重み付きグラフについては,FindSpanningTreeは辺重みの最小和を含む全域木を与える.
- 非連結グラフについては,FindSpanningTreeは各連結成分についての全域木からなる部分グラフを与える.
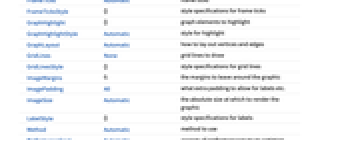
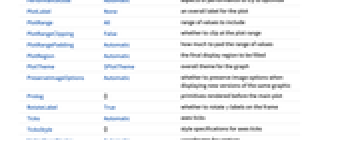
- FindSpanningTreeには,Graphと同じオプションに以下の追加・変更を加えたものが使える. [全オプションのリスト]
-
DistanceFunction Automatic オブジェクトのペアに適用する関数 Method Automatic 使用するメソッド - DistanceFunctionのAutomatic設定には以下の選択肢が含まれる.
-
EuclideanDistance 数のリストの数 EditDistance 文字列 GeoDistance 地理位置 - グラフ g についての距離はGraphDistanceであるとみなされる.
- 次は,Methodの可能な設定である.
-
"Kruskal" 疎な無向グラフをサポートする "MinimumCostArborescence" 有効グラフをサポートする "Prim" 密な無向グラフをサポートする - Automaticのデフォルト設定では,与えられるグラフによって上記の設定が切り替えられる.
全オプションのリスト

例題
すべて開くすべて閉じるスコープ (10)
オプション (5)
EdgeWeight (1)
デフォルトで,辺の重みは,あればその辺のEdgeWeight注釈,なければ1であるとみなされる:
EdgeWeight->weights を使って辺の重みを設定する:
アプリケーション (7)
ある企業がシカゴの周辺地区数ヶ所を結ぶファイバー回路網を計画している.この会社は特定の経路についてのみ敷設権を所有している.これらの経路の中には他より費用がかかることが見込まれるものもある.すべての周辺地区を結び,総費用が最低となる連結経路の部分グラフを求める:
電話会社が戸数10戸の村に電話線を引くことになった.各ノードは家で各家にはその場所がある.電話線を最小にして全戸を繋ぐ方法を求める:
行の項が数ヶ所を除いてほぼ等しい二次元配列がある.![]() は行
は行 ![]() および
および ![]() の異なる項の数を表す.この配列は,完全な行1行と,別の行と異なる項としての他の行すべてを表すことによって,保存することができる.配列の各行を,他のすべての頂点への辺を持ち,異なる項の数を表す重み
の異なる項の数を表す.この配列は,完全な行1行と,別の行と異なる項としての他の行すべてを表すことによって,保存することができる.配列の各行を,他のすべての頂点への辺を持ち,異なる項の数を表す重み ![]() の頂点としてモデル化することができる.最小重み全域木を使って効率的な保存スキームを求める:
の頂点としてモデル化することができる.最小重み全域木を使って効率的な保存スキームを求める:
行1を完全に保存し,残りの行については親と異なる位置と項のみを保存する:
アフリカ諸国すべての地理的中心を繋ぐ国家間幹線道路システムを建設する:
一様ランダム重みのある完全グラフの最小全域木の,期待される大きさを求める:
特性と関係 (2)
テキスト
Wolfram Research (2014), FindSpanningTree, Wolfram言語関数, https://reference.wolfram.com/language/ref/FindSpanningTree.html (2021年に更新).
CMS
Wolfram Language. 2014. "FindSpanningTree." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/FindSpanningTree.html.
APA
Wolfram Language. (2014). FindSpanningTree. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindSpanningTree.html