FindSpanningTree
FindSpanningTree[{v1,v2,…,vn}]
求可最小化 vi 之间总距离的生成树.
求可最小化顶点之间总距离的图 g 的生成树.
FindSpanningTree[{g,v},…]
找到 g 包括顶点 v 的连通分量的生成树.
FindSpanningTree[{vw,…},…]
使用规则 vw 指定图 g.
更多信息和选项


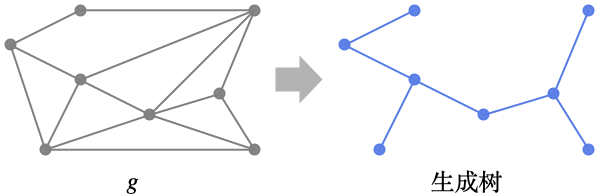
- FindSpanningTree 也被称为最小生成树和最小生成森林.
- 通常用于求没有环的最佳连接.
- FindSpanningTree[{v1,…,vn}] 给出可最小化 vi 之间总距离的顶点为 v1,…,vn 的完全图的生成树.
- 连通图 g 的生成树是 g 的一个子图,是连接 g 的所有顶点的一颗树.
- 对于加权图,FindSpanningTree 给出边权和最小的生成树.
- 对于不连通图,FindSpanningTree 给出一个子图,它由每个连通分量的生成树组成.
- FindSpanningTree 与 Graph 的选项相同,不同之处及更多选项如下所示: [所有选项的列表]
-
DistanceFunction Automatic 应用于成对对象的函数 Method Automatic 使用的方法 - DistanceFunction 的 Automatic 设置包括以下选择:
-
EuclideanDistance 数字列表的个数 EditDistance 字符串 GeoDistance 地理位置 - 对于图 g,距离为 GraphDistance.
- Method 的可能设置包括:
-
"Kruskal" 支持稀疏无向图 "MinimumCostArborescence" 支持有向图 "Prim" 支持稠密无向图 - 使用默认设置 Automatic 时,将根据给定的图在这些方法之间切换.

所有选项的列表


范例
打开所有单元关闭所有单元范围 (10)
选项 (5)
EdgeWeight (1)
默认情况下,如果可用,边的权值取其 EdgeWeight 注释,否则为1:
使用 EdgeWeight->weights 设置边的权值:
应用 (7)
一个公司正在为一些芝加哥郊区筹划光纤网络. 它仅具有将它们的光纤沿某些走廊的优先通行权. 这些走廊中的某一些可能更昂贵. 找到连接走廊的子图,使得与各郊区连接总成本最低:
电话公司的任务是为一个有 10 户人家的村庄提供电话线. 每个节点都是一个房子,每个房子都有一个位置. 找到一种使用最少电话线连接所有房屋的方法:
一个二维数组,各行具有相似的元素,仅在几个地方有区别. ![]() 表示行
表示行 ![]() 和
和 ![]() 的不同元素的数目. 该数组可以如此存储:表示一个整行,而其他各行用不同于另一行的元素表示来存储. 我们可以将各矩阵的行作为顶点进行模拟,其中用边连接每个顶点,用
的不同元素的数目. 该数组可以如此存储:表示一个整行,而其他各行用不同于另一行的元素表示来存储. 我们可以将各矩阵的行作为顶点进行模拟,其中用边连接每个顶点,用 ![]() 的权值表示相异元素的个数. 使用最小权值生成树找到一个有效的存储方案:
的权值表示相异元素的个数. 使用最小权值生成树找到一个有效的存储方案:
属性和关系 (2)
文本
Wolfram Research (2014),FindSpanningTree,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FindSpanningTree.html (更新于 2021 年).
CMS
Wolfram 语言. 2014. "FindSpanningTree." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/FindSpanningTree.html.
APA
Wolfram 语言. (2014). FindSpanningTree. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FindSpanningTree.html 年