FiniteField[p,d]
![]() 個の元からなる有限体を与える.
個の元からなる有限体を与える.
FiniteField[p,f]
![]() が
が ![]() の既約多項式である有限体
の既約多項式である有限体 ![]() を与える.
を与える.
FiniteField[p,…,rep]
"Polynomial"または"Exponential"の体の元表現 rep を使う.


FiniteField
FiniteField[p,d]
![]() 個の元からなる有限体を与える.
個の元からなる有限体を与える.
FiniteField[p,f]
![]() が
が ![]() の既約多項式である有限体
の既約多項式である有限体 ![]() を与える.
を与える.
FiniteField[p,…,rep]
"Polynomial"または"Exponential"の体の元表現 rep を使う.
詳細





- 有限体はガロア(Galois)体としても知られている.
- 有限体は,代数計算,暗号学,符号化理論,組合せ論,代数幾何学,整数論,有限幾何学にしばしば用いられる.
- 体
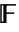 は,4つの算術演算+,-,*,÷がすべてある代数系である.有限体
は,4つの算術演算+,-,*,÷がすべてある代数系である.有限体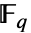 は,素数
は,素数 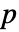 と正の整数
と正の整数 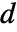 について
について 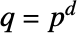 個の元
個の元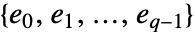 を持つことができる.
を持つことができる. 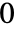 番目の元
番目の元 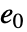 はすべての
はすべての 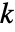 について
について 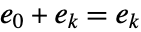 となる加法の単位元で,
となる加法の単位元で,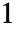 番目の元
番目の元 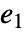 はすべての
はすべての 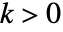 について
について 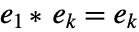 となる乗法の単位元を与える.
となる乗法の単位元を与える.- FiniteFieldElement[,k]または[k]を使って
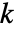 番目の元
番目の元 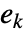 が入手できる.これは
が入手できる.これは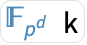 と表示される.
と表示される.
- 同じ体にあるFiniteFieldElementオブジェクトは算術操作によって自動的に結合される.
- 有限体からの係数を持つ多項式には,PolynomialGCD,Factor,Expand,PolynomialQuotientRemainder,Resultantのような多項式操作を使うことができる.有限体からの係数を持つ有理関数には,TogetherおよびCancelを使うことができる.
- Det,Inverse,RowReduce,NullSpace,MatrixRank,LinearSolveのような線形代数操作は,有限体からの項を持つ行列に使うことができる.
- SolveおよびReduceを使って方程式系を有限体上で解くことができる.
- FiniteFieldは"Polynomial"と"Exponential"の異なる2つの表現 rep をサポートする.
- "Polynomial"表現は複素数
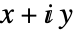 のデカルト表現に似た表現で,加算と減算は簡単だが乗算と除算は少々難しくなる.
のデカルト表現に似た表現で,加算と減算は簡単だが乗算と除算は少々難しくなる. - 表現 次数 d の既約多項式
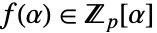 を使って商を持つ体を識別する:
を使って商を持つ体を識別する: -
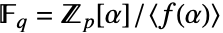
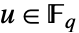 の各元は多項式
の各元は多項式 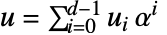 として表される.基底が
として表される.基底が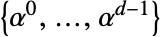 のベクトル
のベクトル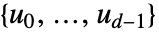 と考えることもできる.
と考えることもできる.- 列挙 元は辞書的順序の逆順に列挙される.
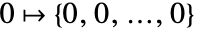 ,
,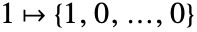 ,…,
,…,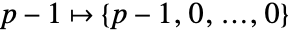 ,…,
,…,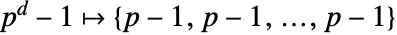
- 操作
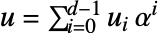 かつ
かつ 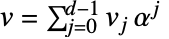 とすると以下になる.
とすると以下になる. 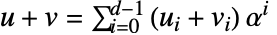 かつ
かつ 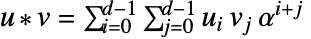
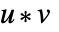 は
は 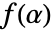 (PolynomialRemainder) を法として簡約されて次数
(PolynomialRemainder) を法として簡約されて次数 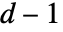 になる.
になる.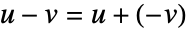 (
(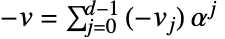 .
. 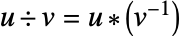 )で乗法の逆元
)で乗法の逆元 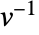 は拡張多項式の最大公約数を使って計算される.
は拡張多項式の最大公約数を使って計算される.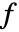 は既約なので,
は既約なので,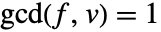 .したがって,多項式
.したがって,多項式 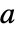 と
と 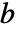 について拡張多項式の最大公約数から
について拡張多項式の最大公約数から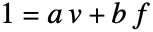 が得られる.
が得られる.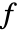 を法として簡約すると
を法として簡約すると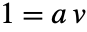 になる.したがって
になる.したがって 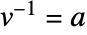 である.
である.- "Exponential"表現は複素数の極表現
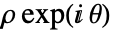 に似た表現で,乗算と除算は簡単だが加算と減算は少々難しくなる.
に似た表現で,乗算と除算は簡単だが加算と減算は少々難しくなる. - 表現 "Polynomial"表現におけるように,この表現も次数 d の既約多項式
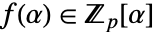 を使うが,
を使うが,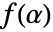 は原始的でもなければならない.
は原始的でもなければならない.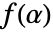 が原始的なので,
が原始的なので,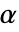 のベキは
のベキは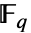 の中の
の中の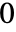 以外のすべての元を表す.
以外のすべての元を表す. -
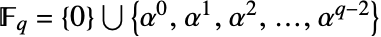
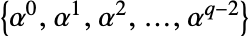 が乗法について巡回群なので,この表現は巡回群表現としても知られている.
が乗法について巡回群なので,この表現は巡回群表現としても知られている.- 列挙 元は指数順に列挙される.
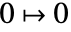 ,
, 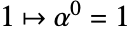 ,
, 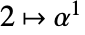 , …,
, …, 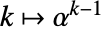 , …,
, …, 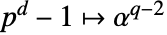
- 操作
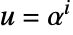 かつ
かつ 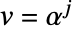 とすると以下になる.
とすると以下になる. ![u *v=alpha^(TemplateBox[{{(, {i, +, j}, )}, {(, {q, -, 1}, )}}, Mod]) u *v=alpha^(TemplateBox[{{(, {i, +, j}, )}, {(, {q, -, 1}, )}}, Mod])](Files/FiniteField.ja/74.png) かつ
かつ 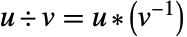
- 反転すると
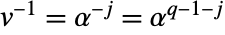 となる.加法と減法については
となる.加法と減法については 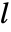 には
には 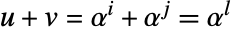 となるような簡単な規則はなく,体のサイズが
となるような簡単な規則はなく,体のサイズが 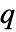 で線形な参照テーブルに格納されている.これによってデータ格納という費用はかかるが操作が速くなる.これはまた"Exponential"表現は大きい体には適していないことも意味している.
で線形な参照テーブルに格納されている.これによってデータ格納という費用はかかるが操作が速くなる.これはまた"Exponential"表現は大きい体には適していないことも意味している. - 表現間の現実的な違いは次の通りである.
- "Polynomial"の作成には時間がかからず,余分なメモリも使わない.大きい体に使えるが操作は若干遅くなる.
- "Exponential"の作成には若干時間がかかり,体の大きさに比例して余分なメモリも必要となる.小さい体に使えて操作は若干速い.
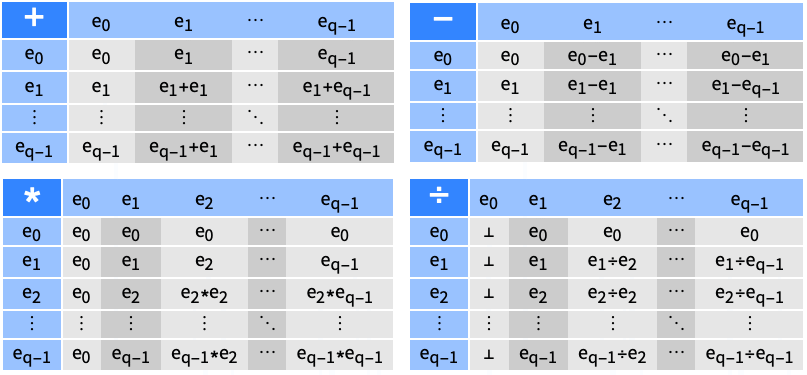
- Information[FiniteField[…], prop]は有限体の特性 prop を与える.次は指定可能な特性である.
-
"Characteristic" 有限体の標数 p "ExtensionDegree"  上の有限体の拡大次数 d
上の有限体の拡大次数 d"FieldSize" 体の元の数 q=pd "FieldIrreducible" 体の構築に使われた多項式関数 f "ElementRepresentation" "Polynomial"または"Exponential"
例題
すべて開く すべて閉じるスコープ (13)
アプリケーション (8)
エラー訂正コードを実装する.![]() ハミングコードは
ハミングコードは ![]() ビットのメッセージを
ビットのメッセージを ![]() ビットシーケンスで符号化し,エラーを1つ修正することができる:
ビットシーケンスで符号化し,エラーを1つ修正することができる:
指数の元表現を使って ![]() を元の数が
を元の数が![]() の有限体とし,
の有限体とし,![]() は
は ![]() を構築するための既約多項式,
を構築するための既約多項式,![]() は
は ![]() の生成元とする:
の生成元とする:
符号化されたメッセージは ![]() の係数リストである.ただし,
の係数リストである.ただし,![]() の係数リストはもとのメッセージである:
の係数リストはもとのメッセージである:
受信したメッセージにエラーがなければ ![]() であり,したがって
であり,したがって ![]() である:
である:
受信したメッセージの位置 ![]() にエラーが1つ含まれていれば
にエラーが1つ含まれていれば ![]() であり,したがって
であり,したがって ![]() である:
である:
受信したメッセージのエラーが1つ以下の場合,復号化されたメッセージは正しい:
任意の素数ベキ ![]() について,次数
について,次数 ![]() の
の ![]() 直交ラテン方陣を構築する.次数
直交ラテン方陣を構築する.次数 ![]() のラテン方陣は,各行各列が
のラテン方陣は,各行各列が ![]() 要素中の各1要素を厳密に1回含む
要素中の各1要素を厳密に1回含む ![]() 配列である.2つの配列を並置して構成された
配列である.2つの配列を並置して構成された ![]() ペアがすべて異なる場合,そのラテン方陣のペアは直交すると言われる:
ペアがすべて異なる場合,そのラテン方陣のペアは直交すると言われる:
![]() のときの総和
のときの総和 ![]() がすべてことなっているなら,整数の有限集合
がすべてことなっているなら,整数の有限集合![]() はSidon集合である.
はSidon集合である.![]() の
の ![]() 個の整数のSidon集合を素数ベキ
個の整数のSidon集合を素数ベキ ![]() について構築する:
について構築する:
アルファベットの ![]() 文字からなる
文字からなる ![]() 次のde Bruijn列は,
次のde Bruijn列は,![]() 文字の各の列が
文字の各の列が ![]() の循環列に厳密に1回現れるようなアルファベットの
の循環列に厳密に1回現れるようなアルファベットの ![]() 文字の循環列
文字の循環列 ![]() である.
である.![]() 文字のアルファベットの
文字のアルファベットの ![]() 次de Bruijn列を,素数ベキ
次de Bruijn列を,素数ベキ ![]() について構築する:
について構築する:
![]() が
が ![]() 文字のアルファベットについての次数
文字のアルファベットについての次数 ![]() のde Bruijn列であることを確認する:
のde Bruijn列であることを確認する:
![]() 行列
行列 ![]() のすべての成分が
のすべての成分が![]() か
か![]() で
で ![]() なら,
なら,![]() はアダマール(Hadamard)行列である.任意の素数ベキ
はアダマール(Hadamard)行列である.任意の素数ベキ ![]() (
(![]() )について次数
)について次数 ![]() のアダマール行列を構築する:
のアダマール行列を構築する:
高度暗号化標準(AES)アルゴリズムで使われている「Rijndael S-Box Step」を実装する.「Nyberg S-Box」と呼ばれる最初の部分は![]() における乗法の逆元を使用する:
における乗法の逆元を使用する:
逆S-BoxがForward S-Boxの逆であることを確認する:
Diffie–Hellman公開鍵の暗号システムを2049ビットの素数で実装する:
2048ビットのメッセージ ![]() を送るために,2番目のユーザは
を送るために,2番目のユーザは ![]() と
と ![]() を送る:
を送る:
デジタル署名スキームを実装する.素数 ![]() を固定して
を固定して![]() の原始元
の原始元 ![]() を求める:
を求める:
メッセージ ![]() のための署名は,
のための署名は,![]() となるような
となるような ![]() より小さい正の整数のペア
より小さい正の整数のペア![]() である.署名の計算には秘密の整数
である.署名の計算には秘密の整数 ![]() の知識が必要である:
の知識が必要である:
特性と関係 (7)
したがって,写像 ![]() はFrobeniusAutomorphismとして知られる体の自己同型である:
はFrobeniusAutomorphismとして知られる体の自己同型である:
FrobeniusAutomorphismを使って ![]() の残りの根を求める:
の残りの根を求める:
![]() 上の次数
上の次数 ![]() の任意の既約多項式は,
の任意の既約多項式は,![]() 個の元がある体で
個の元がある体で ![]() 個の根を持つ:
個の根を持つ:
IrreduciblePolynomialQとModulusp を使って![]() 上における既約性を確かめる:
上における既約性を確かめる:
FactorとExtensionℱ を使って f が ℱ 上における線形係数の積であることを確かめる:
FiniteField[p,1]を使って素体![]() 上で計算する:
上で計算する:
Modの結果と比較する:
Modulusオプションで得られた結果と比較する:
ToFiniteFieldを使って整数係数を有限体の素部分体の元に変換する:
FromFiniteFieldは係数を整数に変換し直す:
テキスト
Wolfram Research (2023), FiniteField, Wolfram言語関数, https://reference.wolfram.com/language/ref/FiniteField.html (2024年に更新).
CMS
Wolfram Language. 2023. "FiniteField." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FiniteField.html.
APA
Wolfram Language. (2023). FiniteField. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteField.html
BibTeX
@misc{reference.wolfram_2025_finitefield, author="Wolfram Research", title="{FiniteField}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteField.html}", note=[Accessed: 16-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finitefield, organization={Wolfram Research}, title={FiniteField}, year={2024}, url={https://reference.wolfram.com/language/ref/FiniteField.html}, note=[Accessed: 16-February-2026]}