FiniteField[p,d]
给出有 ![]() 个元素的有限域.
个元素的有限域.
FiniteField[p,f]
给出有限域 ![]() ,其中
,其中 ![]() 是
是 ![]() 中的不可约多项式.
中的不可约多项式.
FiniteField[p,…,rep]
使用域元素表示法 rep,可以是 "Polynomial" 或者 "Exponential".


FiniteField
FiniteField[p,d]
给出有 ![]() 个元素的有限域.
个元素的有限域.
FiniteField[p,f]
给出有限域 ![]() ,其中
,其中 ![]() 是
是 ![]() 中的不可约多项式.
中的不可约多项式.
FiniteField[p,…,rep]
使用域元素表示法 rep,可以是 "Polynomial" 或者 "Exponential".
更多信息





- 有限域也称为伽罗瓦域.
- 有限域用于代数计算、纠错码、密码学、组合数学、代数几何、数论和有限几何等.
- 域
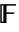 是具有所有四则算术运算(+,-,* 和 ÷)的代数系统. 对于某些质数
是具有所有四则算术运算(+,-,* 和 ÷)的代数系统. 对于某些质数 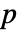 和正整数
和正整数 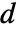 ,有限域
,有限域 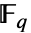 可以有
可以有 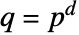 个元素
个元素 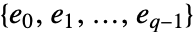 .
. - 第
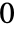 个元素
个元素 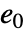 是加法单位元,对于所有
是加法单位元,对于所有 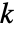 ,
,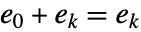 均成立,而第
均成立,而第 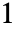 个元素
个元素 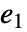 是乘法单位元,对于所有
是乘法单位元,对于所有 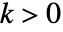 ,
,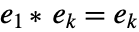 均成立.
均成立. - FiniteFieldElement[,k] 或 [k] 可用于得到第
 个元素
个元素  ,并且格式为
,并且格式为 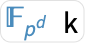 .
.
- 在同一域中的 FiniteFieldElement 对象通过算术运算自动合并.
- 多项式运算,如 PolynomialGCD、Factor、Expand、PolynomialQuotientRemainder 和 Resultant 等,可用于具有有限域系数的多项式. Together 和 Cancel 可用于具有有限域系数的有理函数.
- 线性代数运算,如 Det、Inverse、RowReduce、NullSpace、MatrixRank 和 LinearSolve 等,可用于具有有限域元素的矩阵.
- Solve 和 Reduce 可用于求解有限域上的方程组.
- FiniteField 支持两种不同的表示法 rep:"Polynomial" 和 "Exponential".
- "Polynomial" 表示法类似于复数
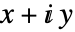 的笛卡尔表示,易于进行加减,但进行乘除则略有难度.
的笛卡尔表示,易于进行加减,但进行乘除则略有难度. - 表示法:它使用 d 次不可约多项式
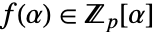 来识别具有商:
来识别具有商: 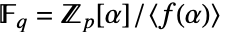 的域.
的域.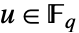 用多项式
用多项式 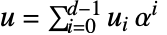 表示. 或者也可以把它当作基为
表示. 或者也可以把它当作基为 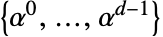 的向量
的向量 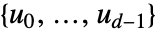 .
. - 枚举: 元素按逆字典顺序枚举:
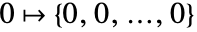 ,
,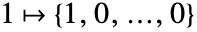 ,…,
,…,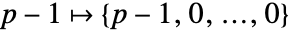 ,…,
,…,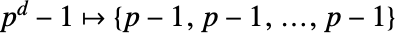
- 运算:令
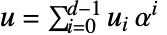 且
且 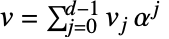 ;则有:
;则有: 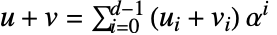 及
及 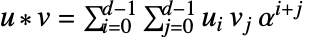
- 且
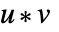 以
以 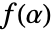 为模(PolynomialRemainder)降低到
为模(PolynomialRemainder)降低到 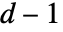 次.
次. 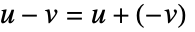 且
且 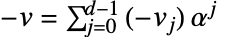 .
. 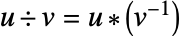 ,乘法逆
,乘法逆 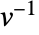 是使用扩展多项式 GCD 计算的. 由于
是使用扩展多项式 GCD 计算的. 由于 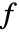 不可约,有
不可约,有 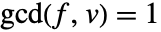 ,因此从扩展多项式 GCD,对于某些多项式
,因此从扩展多项式 GCD,对于某些多项式 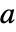 和
和 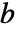 ,有
,有 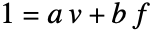 . 通过降低模
. 通过降低模 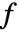 ,得到
,得到 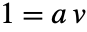 ,因此有
,因此有 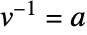 .
. - "Exponential" 表示法类似于复数
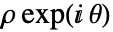 的极坐标表示,易于进行乘除,但进行加减则略有难度.
的极坐标表示,易于进行乘除,但进行加减则略有难度. - 表示法:正如在 "Polynomial" 表示法中,它使用次数为 d 的不可约多项式
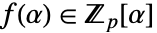 ,但在这种情况下,
,但在这种情况下,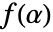 也需要是原函数. 由于
也需要是原函数. 由于 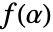 为原函数,
为原函数,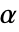 的幂表示
的幂表示 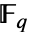 中除了
中除了 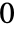 以外的每个元素:
以外的每个元素: -
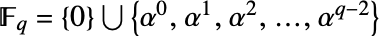
- 该表示法也称为循环群表示法,因为
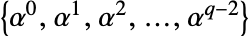 是一个乘法循环群.
是一个乘法循环群. - 枚举:使用幂次序枚举元素:
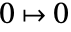 ,
, 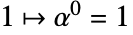 ,
, 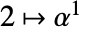 , …,
, …, 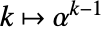 , …,
, …, 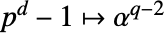
- 运算:令
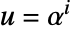 和
和 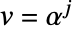 ,则得到:
,则得到: ![u *v=alpha^(TemplateBox[{{(, {i, +, j}, )}, {(, {q, -, 1}, )}}, Mod]) u *v=alpha^(TemplateBox[{{(, {i, +, j}, )}, {(, {q, -, 1}, )}}, Mod])](Files/FiniteField.zh/74.png) 和
和 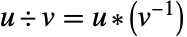
- 并且有倒数关系
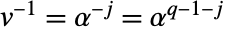 . 对于加法和减法,没有简单规则能够给出
. 对于加法和减法,没有简单规则能够给出 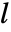 ,使得
,使得 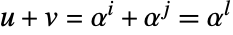 ,因此它存储在查找表中,该表在域大小
,因此它存储在查找表中,该表在域大小 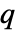 中是线性的. 这使得运算更快,但以存储数据为代价. 这也意味着 "Exponential" 表示法不适用于大型域.
中是线性的. 这使得运算更快,但以存储数据为代价. 这也意味着 "Exponential" 表示法不适用于大型域. - 表示法之间的实际区别是:
- "Polynomial"不需要花时间来创建,不使用额外的内存,适用于大型域,但运算速度稍慢.
- "Exponential" 需要一些时间来创建,使用与域大小成比例的额外内存,适用于小型域但运算速度稍快.
- Information[FiniteField[…], prop] 给出有限域的属性 prop. 可以指定以下属性:
-
"Characteristic" 有限域的特征 p "ExtensionDegree" 有限域在 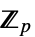 上的扩张度 d
上的扩张度 d"FieldSize" 域的元素个数 q=pd "FieldIrreducible" 用于构造域的多项式函数 f "ElementRepresentation" "Polynomial" 或 "Exponential"
范例
打开所有单元 关闭所有单元范围 (13)
应用 (8)
执行纠错码. ![]() 汉明码将
汉明码将 ![]() 位消息编码为
位消息编码为 ![]() 位序列,并且最多可以纠正一个错误:
位序列,并且最多可以纠正一个错误:
令 ![]() 为使用指数元素表示法的具有
为使用指数元素表示法的具有 ![]() 个元素的有限域,令
个元素的有限域,令 ![]() 是用于构造
是用于构造 ![]() 的不可约多项式,令
的不可约多项式,令 ![]() 为
为 ![]() 的生成器:
的生成器:
当接收到的消息没有错误或有一个错误时,解码后的消息是正确的:
为任意质数幂 ![]() 构造
构造 ![]() 个正交的
个正交的 ![]() 阶拉丁方阵.
阶拉丁方阵. ![]() 阶拉丁方阵是一个
阶拉丁方阵是一个 ![]() 数组,其中每一行和每一列都包含恰好
数组,其中每一行和每一列都包含恰好 ![]() 个元素中的每个元素一次. 如果通过并置两个数组形成的
个元素中的每个元素一次. 如果通过并置两个数组形成的 ![]() 个数对都不同,则称这对拉丁方阵是正交的:
个数对都不同,则称这对拉丁方阵是正交的:
如果 ![]() 时,和
时,和 ![]() 都是不同的,那么一个有限的整数集合
都是不同的,那么一个有限的整数集合 ![]() 是一个西顿(Sidon)集合. 对于质幂
是一个西顿(Sidon)集合. 对于质幂 ![]() ,在
,在 ![]() 中构造一个
中构造一个 ![]() 个整数的西顿集合:
个整数的西顿集合:
对于有 ![]() 个字母的字母表,阶
个字母的字母表,阶 ![]() 的 de Bruijn 序列是字母表中
的 de Bruijn 序列是字母表中 ![]() 个字母的循环序列
个字母的循环序列 ![]() ,使得
,使得 ![]() 个字母的每个序列作为
个字母的每个序列作为 ![]() 的子序列恰好出现一次. 为一个有
的子序列恰好出现一次. 为一个有 ![]() 个字母的字母表构造一个阶数为
个字母的字母表构造一个阶数为 ![]() 的 de Bruijn 序列,取质幂
的 de Bruijn 序列,取质幂 ![]() :
:
验证对于一个有 ![]() 个字母的字母表,
个字母的字母表,![]() 是阶数为
是阶数为 ![]() 的 de Bruijn 序列:
的 de Bruijn 序列:
如果 ![]() 的所有项为
的所有项为 ![]() 或
或 ![]() 且
且 ![]() ,则
,则 ![]() 矩阵
矩阵 ![]() 是哈达玛(Hadamard)矩阵. 为任意素幂
是哈达玛(Hadamard)矩阵. 为任意素幂 ![]() 构建一个阶数为
构建一个阶数为 ![]() 的哈达玛矩阵,其中
的哈达玛矩阵,其中 ![]() :
:
实现高级加密标准(AES)算法中使用的 Rijndael S 盒步骤. 第一部分称为 Nyberg S 盒,使用 ![]() 中的乘法逆:
中的乘法逆:
使用 2049 位素数实现 Diffie–Hellman 公钥密码系统:
属性和关系 (7)
因此映射 ![]() 是一个域自同构,称为 FrobeniusAutomorphism:
是一个域自同构,称为 FrobeniusAutomorphism:
使用 FrobeniusAutomorphism 求 ![]() 的剩余根:
的剩余根:
使用 IrreduciblePolynomialQ 与 Modulusp 验证在 ![]() 上的不可约性:
上的不可约性:
使用 Factor 与 Extensionℱ 验证 f 是线性因子在 ℱ 上的乘积:
使用 FiniteField[p,1] 在质数域 ![]() 上计算:
上计算:
与使用 Mod 获得的结果进行比较:
与使用 Modulus 选项获得的结果进行比较:
使用 ToFiniteField 将整数系数转换为有限域质子域中的元素:
FromFiniteField 将系数转换回整数:
文本
Wolfram Research (2023),FiniteField,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FiniteField.html (更新于 2024 年).
CMS
Wolfram 语言. 2023. "FiniteField." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FiniteField.html.
APA
Wolfram 语言. (2023). FiniteField. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FiniteField.html 年
BibTeX
@misc{reference.wolfram_2025_finitefield, author="Wolfram Research", title="{FiniteField}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteField.html}", note=[Accessed: 03-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_finitefield, organization={Wolfram Research}, title={FiniteField}, year={2024}, url={https://reference.wolfram.com/language/ref/FiniteField.html}, note=[Accessed: 03-February-2026]}