FiniteFieldElement
FiniteFieldElement[ff,ind]
给出索引为 ind 的有限域 ff 的元素.
FiniteFieldElement[ff,{c0,c1,c2,…}]
给出有限域 ff 的元素 c0+c1θ+c2θ2+…,其中 θ 是 ff 的域生成器.
更多信息

- FiniteFieldElement 用于表示 FiniteField 中的元素.
- 同一域中的 FiniteFieldElement 对象通过算术运算自动合并.
- Information[a,prop] 或 a[prop] 给出 FiniteFieldElement 对象 a 的属性 prop. 可以指定以下属性:
-
"Field" a 的环境域 ff "Index" a 的索引 "Coefficients" {c0,c1,c2,…},其中 a=c0+c1θ+c2θ2+… "Characteristic" ff 的特征 p "ExtensionDegree" ff 在 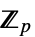 上的扩张度 d
上的扩张度 d"FieldSize" ff 的元素数目 "FieldIrreducible" 用于构造域 ff 的多项式函数 f "ElementRepresentation" "Polynomial" 或者 "Exponential" - MinimalPolynomial[a,x] 给出
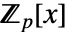 中在 a 处为零的次数最小的一元多项式.
中在 a 处为零的次数最小的一元多项式. - MultiplicativeOrder 给出非零有限域元素的乘法阶.
- PolynomialGCD、Factor、Expand、PolynomialQuotientRemainder 和 Resultant 等多项式运算可用于具有有限域元素系数的多项式. Together 和 Cancel 可用于具有有限域元素系数的有理函数.
- 线性代数运算,如 Det、Inverse、RowReduce、NullSpace、MatrixRank 和 LinearSolve 等,可用于具有有限域元素的矩阵.
- Solve 和 Reduce 可用于求解有限域上的方程组.
范例
打开所有单元关闭所有单元基本范例 (1)
范围 (13)
表示和属性 (4)
使用 Information 提取属性:
算术 (3)
自同构和嵌入 (2)
有限域上的多项式 (2)
有限域上的线性代数 (1)
应用 (8)
执行纠错码. ![]() 汉明码将
汉明码将 ![]() 位消息编码为
位消息编码为 ![]() 位序列,并且可以纠正至多一个错误:
位序列,并且可以纠正至多一个错误:
令 ![]() 为使用指数元素表示法的具有
为使用指数元素表示法的具有 ![]() 个元素的有限域,令
个元素的有限域,令 ![]() 是用于构造
是用于构造 ![]() 的不可约多项式,令
的不可约多项式,令 ![]() 为
为 ![]() 的生成器:
的生成器:
当接收到的消息没有错误或有一个错误时,解码后的消息是正确的:
为任意质数幂 ![]() 构造
构造 ![]() 个正交的
个正交的 ![]() 阶拉丁方阵.
阶拉丁方阵. ![]() 阶拉丁方阵是一个
阶拉丁方阵是一个 ![]() 数组,其中每一行和每一列都包含恰好
数组,其中每一行和每一列都包含恰好 ![]() 个元素中的每个元素一次. 如果通过并置两个数组形成的
个元素中的每个元素一次. 如果通过并置两个数组形成的 ![]() 个数对都不同,则称这对拉丁方阵是正交的:
个数对都不同,则称这对拉丁方阵是正交的:
如果 ![]() 时,和
时,和 ![]() 都是不同的,那么一个有限的整数集合
都是不同的,那么一个有限的整数集合 ![]() 是一个西顿集合(Sidon set). 对于质幂
是一个西顿集合(Sidon set). 对于质幂 ![]() ,在
,在 ![]() 中构造一个
中构造一个 ![]() 个整数的西顿集合:
个整数的西顿集合:
对于有 ![]() 个字母的字母表,阶
个字母的字母表,阶 ![]() 的 de Bruijn 序列是字母表中
的 de Bruijn 序列是字母表中 ![]() 个字母的循环序列
个字母的循环序列 ![]() ,使得
,使得 ![]() 个字母的每个序列作为
个字母的每个序列作为 ![]() 的子序列恰好出现一次. 为一个有
的子序列恰好出现一次. 为一个有 ![]() 个字母的字母表构造一个阶数为
个字母的字母表构造一个阶数为 ![]() 的 de Bruijn 序列,取质幂
的 de Bruijn 序列,取质幂 ![]() :
:
验证对于一个有 ![]() 个字母的字母表,
个字母的字母表,![]() 是阶数为
是阶数为 ![]() 的 de Bruijn 序列:
的 de Bruijn 序列:
如果 ![]() 的所有项为
的所有项为 ![]() 或
或 ![]() 且
且 ![]() ,则
,则 ![]() 矩阵
矩阵 ![]() 是哈达玛(Hadamard)矩阵. 为任意素幂
是哈达玛(Hadamard)矩阵. 为任意素幂 ![]() 构建一个阶数为
构建一个阶数为 ![]() 的哈达玛矩阵,其中
的哈达玛矩阵,其中 ![]() :
:
实现高级加密标准(AES)算法中使用的 Rijndael S 盒步骤. 第一部分称为 Nyberg S 盒,使用 ![]() 中的乘法逆:
中的乘法逆:
使用 2049 位素数实现 Diffie–Hellman 公钥密码系统:
属性和关系 (9)
因此映射 ![]() 是一个域自同构,称为 FrobeniusAutomorphism:
是一个域自同构,称为 FrobeniusAutomorphism:
使用 FrobeniusAutomorphism 求 ![]() 的剩余根:
的剩余根:
使用 MinimalPolynomial 求有限域元素的最小多项式:
使用 IrreduciblePolynomialQ 与 Modulusp 验证在 ![]() 上的不可约性:
上的不可约性:
使用 Factor 与 Extensionℱ 验证 f 是 ![]() 上线性因子的乘积:
上线性因子的乘积:
使用 MultiplicativeOrder 求有限域元素的乘法阶:
使用 FiniteField[p,1] 在质数域 ![]() 上计算:
上计算:
与使用 Mod 获得的结果进行比较:
与使用 Modulus 选项获得的结果进行比较:
使用 FromFiniteFieldIndex 来获取指定索引的域元素:
FiniteFieldIndex 给出了域元素的索引:
文本
Wolfram Research (2023),FiniteFieldElement,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FiniteFieldElement.html (更新于 2024 年).
CMS
Wolfram 语言. 2023. "FiniteFieldElement." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FiniteFieldElement.html.
APA
Wolfram 语言. (2023). FiniteFieldElement. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FiniteFieldElement.html 年