FunctionLayer

FunctionLayer[f]

関数 f を入力に適用するネット層を表す．

詳細とオプション

  • FunctionLayerは，通常のWolfram言語コードからのニューラルネットの定義に使われる．
  • FunctionLayer[f][x]は f[x]と同じように動作する．
  • 関数 f は，配列または配列の連想を生成する配列に対して有効な操作のみを含むべきである．
  • 有効な操作には，数値関数（Plus，Times等），初等関数（Exp，Sqrt，Sin等），数値関数（Min，Round．Ramp等），配列の構築（Table，ConstantArray等），配列操作（Dot，Det，Tr等），記述統計（Mean，StandardDeviation等），距離と類似度（EuclideanDistance，HammingDistance等）が含まれる．ループ構造 （Map，NestList，FoldList等）やリスト操作関数（Part，Reverse等）を使うこともできる．
  • 関数 f は入力として1つの引数しか取るべきではない．引数は，配列または配列の連想でよい．
  • f の引数が一意的な配列なら，f は純関数，記号，あるいはそれらを合成したもので定義することができる．結果の層は"Input"と呼ばれる一意的な入力ポートを持つ．
  • FunctionLayer[Sin[#]&] ⟶
  • f の引数が配列の連想なら，f は名前付きのスロットを使って定義されなければならない．結果の層はスロットに因んで名付けられたポートを持つ．
  • FunctionLayer[#Foo+#Bar&] ⟶
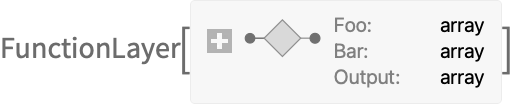
  • FunctionLayerにもまた，FunctionLayer[Apply[f]]という構文を使って複数の引数を持つ関数 f を与えることができる．この場合は，ポートは自動的に命名される．
  • FunctionLayer[Apply[#1+#2&]] ⟶
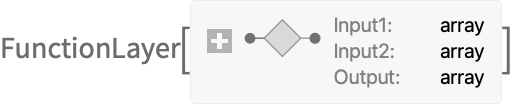
  • f の出力は（一意的なポートに対応する）一意的な配列か（複数のポートに対応する）配列の連想でなければならない．
  • FunctionLayer[<|"Foo"Sin[#],"Bar"#|>&]⟶
  • FunctionLayer[f,"port"shape]をNetGraph等の中で使って，指定されたポートの形状，エンコーダ，あるいはデコーダが指定できる．
  • NetArrayを関数 f の中で使って学習可能パラメータが定義できる．
  • 関数 f はネットに変換される．このネットは層または層のグラフでよい．NetExtractを使って関数の層から層およびパラメータが抽出できる．
  • NetGraph[FunctionLayer[…]]は関数の層をNetGraph[…]に変換する．
  • Information[FunctionLayer[…]]は層についての報告を与える．
  • Information[FunctionLayer[…],prop]はFunctionLayer[…]の特性 prop の値を与える．使用可能な特性はNetGraphのものと同じである．

例題

すべて開くすべて閉じる

例  (2)

配列についてStandardDeviationを計算する層を定義する：

この層は，同じ値を記号として評価する：

もとの関数を抽出する：

StandardDeviationと等しいネットの層を入手する：

StandardDeviationと等しいNetGraphを入手する：

FunctionLayerはNetChainやNetGraphの中で使うことができる：

スコープ  (18)

入出力  (4)

入力ベクトルを取って出力ベクトルを与える関数を計算する層を定義する：

もとの関数を抽出する：

同等のNetGraphを抽出する：

ネットを配列を取って配列の連想を返す関数に変換する：

このネットは関数と同じ値を返す：

ネットを配列の連想を取る関数に変換する：

ネットを配列の連想に適用する：

配列のリストを取る関数をネットに変換する：

このネットを数のリストに適用する：

このネットを配列のリストに適用する：

もとの関数も同じ結果を与える：

正規化  (3)

Normalizeと同じ計算をするNetGraphを定義する：

Standardizeと等しい層を入手する：

カスタム標準化と等しいNetGraphを入手する：

距離  (1)

異なる距離に対応するNetGraphを入手する：

構造  (3)

配列に対して指定された構造操作を行うネット層を入手する：

配列の特定の位置の値を抽出するネット層を入手する：

指定された位置の単位ベクトルを計算するFunctionLayerを作成する：

固定配列と学習可能配列  (1)

固定配列はリストで指定でき，学習可能なパラメータの配列はNetArrayで指定できる：

リスト{0.25,0.75}は，LearningRateMultipliersがゼロの凍結したNetArrayLayerに対応する：

NetArray[{2},"Array"{0.1,0.9}]]は，ペアの学習可能な値が初期化されて{0.1,0.9}になったNetArrayLayerに対応する：

乱数  (5)

2つの入力配列をランダムに選択するネットを作成する：

ランダムに10回選択する：

値がランダムのグレースケールのマスクを画像に加えるネットを作成する：

このネットを画像に適用する：

ランダムな色のマスクを画像に加えるネットを作成する：

このネットを画像に適用する：

ランダムなノイズを画像の画素の行に加えるネットを作成する：

このネットを画像に適用する：

ランダムなノイズを画像の画素に加えるネットを作成する：

このネットを画像に適用する：

エコーのあるデバッグ  (1)

中間計算をネットの出力ポートとして接続する：

このネットを呼び出して値を得る：

EchoTimingはサポートされていない：

考えられる問題  (1)

複数の引数を混在させる関数はサポートされていない：

複数の入力があるネットの定義には，名前付きの入力を使わなければならない：

Wolfram Research (2020), FunctionLayer, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionLayer.html.

テキスト

Wolfram Research (2020), FunctionLayer, Wolfram言語関数， https://reference.wolfram.com/language/ref/FunctionLayer.html.

CMS

Wolfram Language. 2020. "FunctionLayer." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionLayer.html.

APA

Wolfram Language. (2020). FunctionLayer. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionLayer.html

BibTeX

@misc{reference.wolfram_2024_functionlayer, author="Wolfram Research", title="{FunctionLayer}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionLayer.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_functionlayer, organization={Wolfram Research}, title={FunctionLayer}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionLayer.html}, note=[Accessed: 21-November-2024 ]}