-
関連項目
- 関数
- Graph
- GraphPlot
- GraphPlot3D
- PolyhedronData
- KnotData
- LatticeData
-
- 実体タイプ
- Graph
-
- インタープリタタイプ
- Graph
- GraphClass
- ComputedGraph
- 関連するガイド
-
-
関連項目
- 関数
- Graph
- GraphPlot
- GraphPlot3D
- PolyhedronData
- KnotData
- LatticeData
-
- 実体タイプ
- Graph
-
- インタープリタタイプ
- Graph
- GraphClass
- ComputedGraph
- 関連するガイド
-
関連項目


GraphData
詳細









































- GraphDataの指定された entity は,Entity,実体のリスト,あるいは"PetersenGraph"や"FosterCage"のような実体の正規名でよい.
- GraphData[entity]はGraphオブジェクトを与える.
- 指定された property は,EntityProperty,特性の正規名あるいは特性のリストでよい.
- GraphData[patt]は,文字列パターン patt にマッチするすべてのグラフの標準名のリストを与える.
- GraphData[]は標準名がついたすべてのグラフのリストを与える.
- GraphData[All]は使用可能な全グラフを与える.
- GraphData[;;n]は,≤n 個の頂点を持つ標準名の付いた使用可能なグラフのリストを返す.
- GraphData[m;;n]は,頂点数が m 個から n 個までの標準名の付いた使用可能なグラフのリストを返す.
- GraphData[class,nspec]は,指定された class の nspec 個の頂点を持つ使用可能なグラフのリストを返す.
- GraphData["Classes"]は,サポートされているすべてのクラスのリストを返す.
- GraphData["Properties"]は,グラフに利用できる特性のリストを返す.
- GraphData[{n,i},…]は,頂点数が n の i
 番目の単純グラフのデータを与える.
番目の単純グラフのデータを与える. - GraphData[{"type",id},…]は,識別子 id が付いた指定の type のグラフのデータを返す.タイプは一般に文字列で識別子は一般に整数または整数のリストである.
- 基本的なグラフ特性
-
"AdjacencyMatrix" 隣接行列 "EdgeCount" 辺の数の合計 "Edges" 辺 "FaceCount" 面の総数(平面グラフについて) "Faces" 面 "IncidenceMatrix" 結合行列 "VertexCount" 頂点の総数 "Vertices" 頂点 - グラフの連結性に関連した特性
-
"AdjacencyLists" 隣接リスト "ArticulationVertexCount" 関節点の数 "ArticulationVertices" 削除するとグラフが切断されてしまう頂点のリスト "BlockCount" ブロック数 "Blocks" 最小2連結成分 "BridgeCount" 橋の数 "Bridges" 削除するとグラフが切断されてしまう辺のリスト "Connected" 連結 "ConnectedComponentCount" 連結された成分数 "ConnectedInducedSubgraphCount" 誘導された連結部分グラフ数 "ConnectedComponents" 連結成分 "CyclicEdgeConnectivity" 巡回辺連結性 "CyclicEdgeCutCount" 巡回辺切断数 "CyclicEdgeCuts" 巡回辺切断 "Degeneracy" 最大の 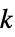 -コアのサイズ
-コアのサイズ"Density" グラフ内の可能な辺の割合 "Disconnected" 非連結 "EdgeConnectivity" グラフを不連続にするために削除する辺の最小数 "EdgeCutCount" 辺切断数 "EdgeCuts" 辺切断 "IncidenceLines" 構成グラフ内の同一線上にある頂点の指標 "LambdaComponents" ラムダ成分 "LuccioSamiComponents" Luccio–Sami成分 "MinimalEdgeCutCount" 最小辺切断数 "MinimalEdgeCuts" 最小辺切断 "MinimalVertexCutCount" 最小頂点切断数 "MinimalVertexCuts" 最小頂点切断 "MinimumCyclicEdgeCutCount" 最小巡回辺切断数 "MinimumCyclicEdgeCuts" 最小巡回辺切断 "MinimumEdgeCutCount" 最小辺切断数 "MinimumEdgeCut" 最小辺切断 "MinimumVertexCutCount" 最小頂点切断数 "MinimumVertexCuts" 最小頂点切断 "MinorCount" グラフマイナーの数 "SpanningTrees" 全域木 "Strength" グラフ強度 "Toughness" グラフのタフネス "Triangulated" 三角化(最大限に平面的) "VertexConnectivity" グラフを不連続にするために削除する頂点の最小数 - 次は,グラフマイナーに関連した特性である.
-
"HadwigerNumber" Hadwiger数 "MinorCount" グラフマイナーの数 - グラフの表示に関連した特性
-
"EmbeddingClasses" 埋込みのためのクラスタグのリスト "Embeddings" "AllVertexCoordinates"の代替名 "Graph" グラフオブジェクト "Graphics" グラフィックス "Graphics3D" 3Dグラフィックス "Image" 画像 "MeshRegion" メッシュ領域 "Polyhedron" 多面体 "VertexCoordinates" デフォルトレイアウトの頂点座標 - リストタイプの出力に関連した注釈可能特性
-
"AdjacencyMatrix","outputtype" 1つまたはすべての隣接行列または可能なすべての隣接行列数 "ConnectedComponents","outputtype" グラフ,リスト,数,変数のリスト,頂点のリストとしての連結成分 "Cycles","outputtype" 無向閉路,有向閉路,あるいは閉路の数 "Edges","outputtype" リストとしての辺,辺のリスト,指標ペアのリスト,規則のリスト,グラフィックス,あるいは辺の数 "EulerianCycles","outputtype" 無向オイラー閉路,有向オイラー閉路,あるいはオイラー閉路の数 "Faces","outputtype" リストとしての面,指標リスト,グラフィックス,あるいは面の数 "HamiltonianCycles","outputtype" 無向ハミルトン閉路,有向ハミルトン閉路,あるいはハミルトン閉路の数 "HamiltonianPaths","outputtype" 無向ハミルトン路,有向ハミルトン路,あるいはハミルトン路の数 "HamiltonianWalks","outputtype" 無向ハミルトンウォーク,有向ハミルトンウォーク,あるいはハミルトンウォークの数 "VertexCoordinates","outputtype" 1つあるいはすべての頂点座標,または埋込みの数 "Vertices","outputtype" リストとしての頂点,指標付きの座標規則のリスト,グラフィックス,あるいは頂点数 - グラフ多項式を表す純関数を与える特性
-
"CharacteristicPolynomial" 隣接行列の固有多項式 "ChordlessCyclePolynomial" 弦がない閉路の数を長さで数えるように符号化する多項式 "ChromaticPolynomial" 彩色多項式 "CliquePolynomial" クリーク多項式 "CoboundaryPolynomial" 双対境界多項式 "ComplementChordlessCyclePolynomial" 補グラフ中の弦がない閉路の数を長さで数えるように符号化する多項式 "ComplementOddChordlessCyclePolynomial" 補グラフ中の弦がない奇数の閉路の数を長さで数えるように符号化する多項式 "ConnectedDominationPolynomial" 連結主多項式 "ConnectedInducedSubgraphPolynomial" 誘導された連結部分グラフ多項式 "CyclePolynomial" 閉路多項式 "CyclicEdgeCutPolynomial" 巡回辺切断多項式 "DetourPolynomial" 迂回行列の固有多項式 "DistancePolynomial" 距離多項式 "DominationPolynomial" 支配多項式 "EdgeCoverPolynomial" 辺被覆多項式 "EdgeCutPolynomial" 辺切断多項式 "FlowPolynomial" フロー多項式 "IdiosyncraticPolynomial" 特異なタット(Tutte)多項式 "IndependencePolynomial" 独立多項式 "IrredundancePolynomial" 非冗長多項式 "LaplacianPolynomial" ラプラス多項式 "MatchingGeneratingPolynomial" マッチング生成多項式 "MatchingPolynomial" マッチング多項式 "MaximalCliquePolynomial" 極大クリークの数をサイズで符号化する多項式 "MaximalIndependencePolynomial" 極大独立頂点集合の数をサイズで符号化する多項式 "MaximalIrredundancePolynomial" 非冗長極大集合の数をサイズで符号化する多項式 "MaximalMatchingGeneratingPolynomial" 極大辺集合の数をサイズで符号化する多項式 "MinimalConnectedDominationPolynomial" 極小接続支配集合の数をサイズで符号化する多項式 "MinimalDominationPolynomial" 極小支配集合数をサイズで符号化する多項式 "MinimalEdgeCoverPolynomial" 極小辺被覆数をサイズで符号化する多項式 "MinimalEdgeCutPolynomial" 最小辺切断数をサイズで符号化する多項式 "MinimalTotalDominationPolynomial" 極小総合支配集合の数をサイズで符号化する多項式 "MinimalVertexCoverPolynomial" 極小頂点被覆数をサイズで符号化する多項式 "MinimalVertexCutPolynomial" 最小頂点切断数をサイズで符号化する多項式 "OddChordlessCyclePolynomial" 奇数の弦のない閉路の数を長さで符号化する多項式 "PathPolynomial" 経路多項式 "QChromaticPolynomial" Q-彩色多項式 "RankPolynomial" 階数多項式 "ReliabilityPolynomial" 信頼性多項式 "SigmaPolynomial" 降階乗基における彩色多項式 "TotalDominationPolynomial" 総合支配集合の数をサイズで符号化する多項式 "TuttePolynomial" タット多項式 "VertexCoverPolynomial" 頂点被覆多項式 "VertexCutPolynomial" 頂点切断数をサイズで符号化する多項式 - 彩色に関連するグラフ特性
-
"ChromaticInvariant" 彩色不変量 "ChromaticNumber" 彩色数 "ChromaticPolynomial" 彩色多項式 "ChromaticRoots" 彩色根 "CyclicChromaticNumber" 循環彩色数 "EdgeChromaticNumber" 辺の彩色数 "FractionalChromaticNumber" 分数彩色数 "FractionalEdgeChromaticNumber" 辺の分数彩色数 "MinimumVertexColoringCount" 最小頂点彩色の数 "MinimumVertexColorings" 最小辺彩色 "MinimumEdgeColoring" 辺の色付けに使う最小数の色 "MinimumWeightFractionalColoring" 最小の重み付き分数彩色数 "QChromaticPolynomial" Q-彩色多項式 "WeisfeilerLemanDimension" Weisfeiler–Leman次元 - グラフ指標特性
-
"ABCIndex" 原子結合接続性指標 "ArithmeticGeometricIndex" 算術幾何指標 "BalabanIndex" バラバン(Balaban)指標 "CircuitRank" 非巡回にするために除去する辺の最小数 "DetourIndex" 迂回指標 "HararyIndex" Harary指標 "HosoyaIndex" 細矢指標 "KirchhoffIndex" キルヒホフ指標 "KirchhoffSumIndex" キルヒホフの総和指標 "MolecularTopologicalIndex" 分子位相(第2Schultz)指標 "RandicIndex" Randić指標 "SomborIndex" Sombor指標 "StabilityIndex" 安定指標 "TopologicalIndex" 位相(第1Schultz)指標 "WienerIndex" ウィーナー(Wiener)指標 "WienerSumIndex" ウィーナーの総和指標 "ZagrebIndex1" 最初のZagrebインデックス "ZagrebIndex2" 2番目のZagrebインデックス - 行列グラフ特性
-
"ABCMatrix" 原子結合接続行列 "AdjacencyMatrix" 隣接行列 "ArithmeticGeometricMatrix" 算術幾何行列 "DetourMatrix" 最長経路距離の行列 "DistanceMatrix" 距離行列 "IncidenceMatrix" 結合行列 "LaplacianMatrix" ラプラス行列 "MaximumFlowMatrix" 最大フロー行列 "MinimumCostFlowMatrix" 最小費用フロー行列 "NormalizedLaplacianMatrix" 正規化ラプラス行列 "RandicMatrix" Randić行列 "ResistanceMatrix" 単位抵抗辺の頂点ペア間の抵抗 "SomborMatrix" Sombor行列 - 局所グラフの特性
-
"ChordCount" 弦の数 "Chords" 弦 "Curvatures" 曲率 "IsolatedPointCount" 孤立点の数 "IsolatedPoints" 次数0の頂点 "LeafCount" 葉の数 "Leaves" 次数1の頂点 - 大域グラフの特性
-
"Anarboricity" 結合するともとのグラフになる九環性辺素部分グラフの最大数 "ApexCount" 頂点数 "Apices" 除去するとグラフが平面グラフになる頂点のリスト "Arboricity" 結合するともとのグラフになる非環式辺素部分グラフの最小数 "Center" グラフ離心率が半径と等しい頂点の指標 "Circumference" グラフの外周 "Coarseness" 線素非平面部分グラフの最大数 "Corank" 辺の数 − 頂点数 + 連結された成分数 "Degeneracy" グラフの縮退 "DegreeSequence" 最小のものから最大のものへと並べられた頂点次数 "DeterminedByResistance" 他のどのグラフも同じ抵抗のマルチセットを共有しない "DeterminedBySpectrum" 他のどのグラフもスペクトルを共有しない "Diameter" グラフの直径 "Eccentricities" 各頂点の離心率 "FractionalArboricity" 分数樹化数 "IntersectionArray" 交点配列 "LinearArboricity" 線形樹化数 "MaximumLeafNumber" 任意の全域木の木の葉の最大数 "MaximumVertexDegree" 最大頂点次数 "MeanCurvature" 平均曲率 "MeanDistance" 頂点間の平均距離 "MinimumLeafNumber" 任意の全域木の葉の最小数 "MinimumVertexDegree" 最小頂点次数 "Periphery" グラフ離心率が直径と等しい頂点の指標 "Pseudoarboricity" 擬似樹化数 "QuadraticEmbeddingConstant" 二次的埋込み定数 "Rank" 頂点数から連結された成分数を引いたもの "RegularParameters" 頂点の共通近傍数を表すパラメータ "Skewness" 除去するとグラフが平面グラフになる辺の最小数 "SpanningTreeCount" 全域木の数 "StarArboricity" スター樹化数 "Thickness" 結合するともとのグラフになる平面部分グラフの最小数 "TreeNumber" グラフの辺を被覆する木の最小数 "Triameter" グラフTriameter (グラフ直径の一般化) "VertexDegrees" 頂点次数 - スペクトルグラフの特性
-
"ABCEnergy" 原子結合接続性のエネルギー "ABCSpectralRadius" 原子結合接続性スペクトルのエネルギー "AlgebraicConnectivity" ラプラス行列の2番目に小さい固有値 "ArithmeticGeometricEnergy" 算術幾何エネルギー "ArithmeticGeometricSpectralRadius" 算術幾何スペクトル半径 "Energy" グラフのエネルギー "LaplacianSpectralRadius" ラプラシアンスペクトル半径 "LaplacianSpectralRatio" ラプラシアンスペクトル比 "LaplacianSpectrum" ラプラス行列の固有値 "RandicEnergy" Randićエネルギー "SomborEnergy" Somborエネルギー "SomborSpectralRadius" Somborスペクトル半径 "SpectralRadius" スペクトル半径 "Spectrum" 隣接行列の固有値 "SpectrumSignature" 隣接行列の固有値の合計 - ラベル付きグラフ特性
-
"AverageDisorderNumber" 平均混乱数 "DisorderNumber" 混乱数 "ErdosSequence" Erdős数列 "GracefulLabelingCount" 基本的に異なる優美ラベリングの数 "GracefulLabelings" 基本的に異なる優美ラベリング "IrregularityStrength" 不規則性の強さ "PinnacleSetCount" ピナクル集合の数 "PinnacleSets" ピナクル集合 "RadioLabelingCount" 基本的に異なる最適ラジオラベリングの数 "RadioLabelings" 基本的に異なる最適ラジオラベリング "RadioNumber" ラジオ番号 - グラフの構築特性には以下がある.
-
"AssemblyNumber" アセンブリ数 "ConstructionNumber" 構築番号 - 位相的グラフ特性
-
"CrossingNumber" グラフの埋込みにおける最小交差数 "Dimension" グラフの次元 "Genus" 辺の交差を含まない埋込みを与えるハンドルの最小数 "KleinBottleCrossingNumber" クラインの壺の埋込みにおける最小交差数 "LocalCrossingNumber" 局所交差数 "MapNumber" 写像数 "MetricDimension" 距離次元 "ProjectivePlaneCrossingNumber" 射影平面埋込みにおける最小交差数 "RectilinearCrossingNumber" 直線埋込みにおける最小交差数 "RectilinearLocalCrossingNumber" 直線局所交差数 "ToroidalCrossingNumber" 環状面埋込みにおける最小交差数 - クリーク関連特性
-
"CliquePolynomial クリーク多項式 "Cliques クリーク "BicliqueNumber" バイクリークの数 "BipartiteDimension" 二部次元 "CliqueCount" クリークの数 "CliqueCoveringNumber" 頂点集合を覆うために必要な最大クリークの最小数 "CliqueNumber" 最大クリーク中の頂点数 "DelsarteCliqueCount" デルサルト(Delsarte)クリークの数 "DelsarteCliques デルサルト境界が達成される距離正規グラフのクリーク "FractionalCliqueNumber" 非整数クリーク数 "LowerCliqueNumber" 最小極大クリークのサイズ "MaximalCliqueCount" 明確な極大クリークの数 "MaximalCliquePolynomial" 極大クリークサイズの合計を符号化する多項式 "MaximalCliques" 極大クリーク "MaximumCliqueCount" 極大クリークの数 "MaximumCliques" 最大クリーク "MinimumCoveringsByMaximalCliques" 最大クリークによる最小被覆 "MinimumCoveringsByMaximalCliquesCount" 最大クリークによる最小被覆数 "SimplexGraph" シンプレックスグラフ - 被覆関連特性
-
"CliqueCoveringNumber" 頂点集合を覆うために必要な最大クリークの最小数 "EdgeCoverCount" 辺被覆の数 "EdgeCoverNumber" 最小辺被覆のサイズ "EdgeCoverPolynomial" 辺被覆多項式 "EdgeCovers" 辺被覆 "MinimalEdgeCoverCount" 極小辺被覆の数 "MinimalEdgeCoverPolynomial" 極小辺被覆サイズを符号化する多項式 "MinimalEdgeCovers" 極小辺被覆 "MinimalVertexCoverCount" 極小頂点被覆の数 "MinimalVertexCoverPolynomial" 極小頂点被覆サイズの合計を符号化する多項式 "MinimalVertexCovers" 極小頂点被覆 "MinimumCliqueCoveringCount" 最小クリーク被覆の数 "MinimumCliqueCoverings" 最小クリーク被覆 "MinimumEdgeCoverCount" 最小辺被覆(マッチする)の数 "MinimumEdgeCovers" 最小辺被覆(マッチする) "MinimumPathCoveringCount" 最小経路被覆の数 "MinimumPathCoverings" 最小経路被覆 "MinimumVertexCoverCount" 最小頂点被覆の数 "MinimumVertexCovers" 最小頂点被覆 "PathCoveringNumber" 経路被覆数 "VertexCoverCount" 頂点被覆の数 "VertexCoverNumber" 最小頂点被覆のサイズ "VertexCoverPolynomial" 頂点被覆多項式 - 独立集合関連特性
-
"BipartiteDimension" 二部次元 "EdgeIndependenceNumber" 独立辺集合のサイズの合計 "FractionalIndependenceNumber" 分数独立数 "IndependenceNumber" 最大独立頂点集合のサイズ "IndependencePolynomial" 独立多項式 "IndependenceRatio" 独立比 "IndependentEdgeSetCount" 独立辺集合の数 "IndependentEdgeSets" 独立辺集合 "IndependentVertexSetCount" 独立頂点集合の数 "IndependentVertexSets" 独立頂点集合 "IntersectionNumber" 交点数 "LowerIndependenceNumber" 最小の最大独立頂点集合の大きさ "LowerMatchingNumber" 最小の最大独立辺集合の大きさ "MatchingGeneratingPolynomial" マッチ生成多項式 "MatchingNumber" マッチ生成多項式の次数 "MatchingPolynomial" マッチ生成多項式 "MaximalIndependencePolynomial" 極大独立頂点集合の数をサイズで符号化する多項式 "MaximalIndependentEdgeSetCount" 極大独立辺集合(マッチする)の数 "MaximalIndependentEdgeSets" 極大独立辺集合(マッチする) "MaximalIndependentVertexSetCount" 極大独立頂点集合の数 "MaximalIndependentVertexSets" 極大独立頂点集合 "MaximalMatchingGeneratingPolynomial" 極大独立変辺集合の数をサイズで符号化する多項式 "MaximumIndependentEdgeSetCount" 最大独立辺集合(マッチする)の数 "MaximumIndependentEdgeSets" 最大独立辺集合(マッチする) "MaximumIndependentVertexSetCount" 最大独立頂点集合の数 "MaximumIndependentVertexSets" 最大独立頂点集合 - 非冗長集合関連特性
-
"IrredundanceNumber" (下方)非冗長性番号 "IrredundancePolynomial" 非冗長性多項式 "IrredundantSetCount" 非冗長集合数 "IrredundantSets" 非冗長集合 "MaximalIrredundancePolynomial" 極大非冗長集合の合計を符号化する多項式 "MaximalIrredundantSetCount" 極大非冗長集合数 "MaximalIrredundantSets" 極大非冗長集合 "MaximumIrredundantSetCount" 最大非冗長集合数 "MaximumIrredundantSets" 最大非冗長集合 "UpperIrredundanceNumber" 頂点の最大非冗長集合のサイズ - 支配集合関連特性
-
"CodominatingGraphs" 同じ支配多項式を共有するグラフ "ConnectedDominatingSetCount" 連結支配集合数 "ConnectedDominatingSets" 連結支配集合 "ConnectedDominationNumber" 連結支配集合の可能な最小サイズ "ConnectedDominationPolynomial" 連結支配集合のサイズを符号化する多項式 "DomaticNumber" グラフのDomatic分割における互いに素な支配集合の最大数 "DominatingSetCount" 支配集合数 "DominatingSets" 支配集合 "DominationNumber" 可能な最小の支配集合サイズ "DominationPolynomial" 支配集合のサイズの合計を符号化する多項式 "DominationRoots" 支配多項式の根 "MinimalConnectedDominatingSetCount" 極小連結支配集合の数 "MinimalConnectedDominatingSets" 極小連結支配集合 "MinimalConnectedDominationPolynomial" 極小連結支配集合のサイズの合計を符号化する多項式 "MinimalDominatingSetCount" 極小支配集合数 "MinimalDominatingSets" 極小支配集合 "MinimalDominationPolynomial" 極小支配集合サイズの合計を符号化する多項式 "MinimalTotalDominatingSetCount" 総極小支配集合数 "MinimalTotalDominatingSets" 総極小支配集合 "MinimalTotalDominationPolynomial" 総極小支配集合サイズの合計を符号化する多項式 "MinimumConnectedDominatingSetCount" 最小連結支配集合数 "MinimumConnectedDominatingSets" 最小連結支配集合 "MinimumDominatingSetCount" 最小支配集合数 "MinimumDominatingSets" 最小支配集合 "MinimumTotalDominatingSetCount" 最小総支配集合数 "MinimumTotalDominatingSets" 最小総支配集合 "TotalDominatingSetCount" 総支配集合数 "TotalDominatingSets" 総支配集合 "TotalDominationNumber" 最小可能総支配集合のサイズ "TotalDominationPolynomial" 総支配集合サイズの合計を符号化する多項式 "UpperDominationNumber" 最大の最大支配集合の大きさ - 対称性関連特性
-
"ArcTransitivity" s 弧推移グラフにおける極大次数 s "AutomorphismCount" 頂点自己同型群の次数 "AutomorphismGroup" グラフの自己同型置換群 "Automorphisms" グラフの自己同型写像に対応する置換のリスト "CanonicalPolyhedronDistinctEdgeLengthCount" 対応する正準多面体における他と異なる長さの辺の数 "CayleyGraphGeneratingGroupNames" ケイリー(Cayley)グラフとしてグラフを生成する群の名称 "CayleyGraphGeneratingGroups" ケイリーグラフとしてグラフを生成する群 "DistinguishingNumber" 識別数 "FixingNumber" Fxing Number "MinimumDistinguishingLabelingCount" 最小識別ラベル付けの数 "MinimumDistinguishingLabelings" 最小識別ラベル付け "PlanarEmbeddingCount" 平面埋込みの数 "SymmetricallyDistinctFaceCount" 対称的に区別できる面の数 "SymmetricallyDistinctFaces" 対称的に区別できる面の代表のリスト "SymmetricallyDistinctVertexPairCount" 対称的に区別できる頂点ペアの数 "SymmetricallyDistinctVertexPairSignature" 対称的に区別できる頂点ペアのシグネチャ "SymmetricallyDistinctVertices" 対称的に区別できる頂点の代表のリスト "SymmetricallyDistinctVertexCount" 対称的に区別できる頂点数 "SymmetricallyEquivalentFaces" 対称的に等しい面のリスト "SymmetricallyEquivalentVertices" 対称的に等しい頂点のリスト - 情報関連特性
-
"Bandwidth" グラフのバンド幅 "BroadcastTime" グラフの放送時間 "BroadcastTimes" 頂点放送時間のリスト "BurningNumber" 燃焼数 "CheegerConstant" Cheeger定数 "Conductance" グラフ伝導性 "CoolingNumber" 冷却数 "Gonality" 最小被覆葉数 "Likelihood" グラフが乱数と対応する頂点 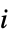 部分集合の選択によって生成される確率
部分集合の選択によって生成される確率"LovaszNumber" Lovász数(Shannon容量の推定) "Pathwidth" グラフのページ幅 "PebblingNumber" ペブリング数 "ScrambleNumber" スクランブル数 "ShannonCapacity" グラフで表された伝達モデルにおける実質的なアルファベットのサイズ "TreeDepth" 木の深さ "Treewidth" グラフの木の幅 - 経路および閉路関連特性
-
"ChordlessCycleCount" 最低でも長さが4の弦がない閉路の数 "ChordlessCyclePolynomial" 弦がない閉路の合計を長さで符号化する多項式 "ChordlessCycles" 最低でも長さが4の弦がない閉路 "ComplementChordlessCycleCount" 補グラフ中の弦がない閉路の数 "ComplementChordlessCyclePolynomial" 補グラフの弦がない閉路の合計数を長さで符号化する多項式 "ComplementChordlessCycles" グラフ中の長さが最低4の弦がない閉路 "ComplementOddChordlessCycleCount" 補グラフの弦がない奇閉路の数 "ComplementOddChordlessCyclePolynomial" 補グラフの弦がない奇閉路の合計を長さで符号化する多項式 "ComplementOddChordlessCycles" 最低でも長さが4の補グラフの弦がない奇閉路 "CubeGraph" グラフキューブ "CycleCount" 識別可能閉路の数 "CyclePolynomial" 閉路多項式 "Cycles" 閉路のリスト "EulerianCycleCount" 識別可能なオイラー閉路数 "EulerianCycles" オイラー閉路のリスト "FaceSignature" 面の長さの合計 "Girth" 最短閉路の長さ "HamiltonDecompositionCount" ハミルトン分解の数 "HamiltonDecompositions" 辺集合をハミルトン閉路にするためのパーティション "HamiltonianCycleCount" 識別可能なハミルトン閉路の数 "HamiltonianCycles" ハミルトン閉路のリスト "HamiltonianNumber" 最短ハミルトンウォークの長さ "HamiltonianPathCount" 識別可能なハミルトン路の数 "HamiltonianPaths" ハミルトン路のリスト "HamiltonianWalkCount" 識別可能なハミルトンウォークの数 "HamiltonianWalks" ハミルトンウォークのリスト "HexagonCount" 六角閉路の数 "KCyclicIndices" グラフに 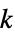 番目の
番目の 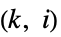 巡回グラフのラベルを付ける指標
巡回グラフのラベルを付ける指標 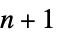
"LCFSignature" 可能なすべてのLCFシグニチャの次数の合計 "LongestCycleCount" 最長閉路の数 "LongestCycles" 最長閉路 "LongestPathCount" 最長経路数 "LongestPathLength" 最長経路の長さ "LongestPaths" 最長経路 "MinimumPathCoveringCount" 最小経路被覆の数 "MinimumPathCoverings" 最小経路被覆 "OddChordlessCycleCount" 長さが3より大きい弦のない奇閉路の数 "OddChordlessCyclePolynomial" 奇数の弦がない閉路数の長さによる合計で符号化する多項式 "OddChordlessCycles" 奇数長が3より大きい弦がない閉路 "PathCount" 区別可能な経路の数 "PathCoveringNumber" 経路被覆数 "PathPolynomial" 経路多項式 "PathPolynomialMatrix" 経路多項式の行列関数 "Paths" 経路のリスト "PentagonCount" 五角閉路の数 "Radius" グラフ半径 "SquareCount" 四角閉路の数 "SquareGraph" 正方形グラフ "TriangleCount" 三角閉路の数 - グラフ中心性
-
"BetweennessCentralities" 媒介中心性 "ClosenessCentralities" 接近中心性 "DegreeCentralities" 頂点次数 "EccentricityCentralities" 頂点中心性の逆数 "EdgeBetweennessCentralities" 辺媒介中心性 "EigenvectorCentralities" 固有ベクトル中心性 "HITSCentralities" ハブ中心性 "KatzCentralities" Katz中心性 "LinkRankCentralities" リンクランク中心性 "PageRankCentralities" ページランク中心性 "RadialityCentralities" 放射中心性 "StatusCentralities" 地位中心性 - グラフのクラスタ化係数
-
"GlobalClusteringCoefficient" 大域的クラスタリング係数 "LocalClusteringCoefficients" 局所的クラスタリング係数 "MeanClusteringCoefficient" 平均クラスタリング係数 - 命名関連の特性
-
"AlternateNames" 代りの英語名 "AlternateStandardNames" 代りの標準Wolfram言語名 "Entity" グラフ実体 "Name" 英語名 "Names" 英語名と代替名 "StandardName" 標準的なWolfram言語での名前 "StandardNames" 標準的なWolfram言語での名前と代替名 - 表記関連特性
-
"HouseOfGraphID" 「House of Graphs」の識別子 "LCFNotations" ハミルトン閉路に基づいた埋込みのグラフの表記 "Notation" グラフに使われる主な表記 "NotationRules" グラフ指定の表記規則 "WikidataID" ウィキペディアID - GraphData["class"]は,指定したクラスでの名前付きグラフのリストを返す.GraphData[name,"class"]は,name に対応するグラフが指定のクラスにあるかどうかによってTrueまたはFalseを返す.
- GraphData[name,"Classes"]は,name に対応するグラフが現れるクラスのリストを返す.
- グラフの基本クラス
-
"Bipartite" 二部(各辺で2つの成分が繋がれている) "Nonplanar" 非平面(交点が必要) "Nonsimple" 非単純グラフ "Planar" 平面(交点はない) "Simple" 単純グラフ(ラベルなし,無向) "Tree" 木(閉路ではない) - 交点に基づくクラス
-
"Apex" 頂点グラフ "CriticalNonplanar" 任意の頂点を削除すると平面グラフになる非平面グラフ "Doublecross" 交点数 2 "DoubleToroidal" 種数 2 "IntrinsicallyLinked" 絡み目内在 "LinklesslyEmbeddable" リンクを含まないように埋込み可能 "Map" 写像グラフ "Nonplanar" 交点数 ≥ 1 "NotUniquelyEmbeddable" 球面上に一意には埋込み不可 "Planar" 交点数 0 "Pretzel" 種数 3 "Singlecross" 交点数 1 "Toroidal" トーラスに最小限に埋込み可能 "UniquelyEmbeddable" 球面上に一意には埋込み可 - 頂点の次数に基づくクラス
-
"Cubic" 各頂点は次数3 "HighlyIrregular" 各頂点の近傍は異なる頂点次数を持つ "Multigraphic" 一つあるいはそれ以上の他のグラフが次数列を共有する "Octic" 各頂点は次数8 "Quartic" 各頂点は次数4 "QuasiRegular" 他の頂点より1次数上の一つの頂点を除いて各頂点は同じ次数 "Quintic" 各頂点は次数5 "Regular" 各頂点の次数が等しい "Septic" 各頂点は次数7 "Sextic" 各頂点は次数6 "Switchable" 辺を切り替えることで同じ次元のシーケンスを持つ他のグラフに削減可能 "TwoRegular" 各頂点は次数2 "Unigraphic" 次数列を共有するグラフはない "Unswitchable" 切替え不可能 - 走査に基づくクラス
-
"Acyclic" 閉路がない "AlmostHamiltonian" ハミルトン数が 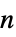 の
の 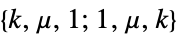 ノードグラフ
ノードグラフ"AlmostHypohamiltonian" ほぼハミルトングラフ "Antipodal" 各頂点が厳密に一つの最大距離頂点を持つ "Bridged" 少なくとも1つの橋を含む "Bridgeless" 橋がない "Chordal" 長さが少なくても4の弦がない閉路がない "Chordless" 弦なし "Cyclic" 少なくとも1つの閉路を含む "Eulerian" すべての辺を1回ずつ含む閉路を持つ "Geodetic" 任意の2つの頂点間に一意的な最短経路を持つ "HamiltonConnected" すべての頂点ペアがハミルトン経路の境界を示す "HamiltonDecomposable" 辺集合を分割するとハミルトン閉路になる "Hamiltonian" すべての頂点を1回ずつ含む閉路を持つ "HamiltonLaceable" 2つに別れた端点を持つハミルトン連結 "HStarConnected" ハミルトン連結またはハミルトン連結可能(Hamilton‐laceable) "Hypohamiltonian" 頂点を1つ削除したグラフはハミルトングラフである "Hypotraceable" 頂点を1つ削除したグラフはトレースできる "KempeCounterexample" ケンペ(Kempe)の4色アルゴリズムの反証 "MaximallyNonhamiltonian" 極大限にハミルトンではない "Median" メディアングラフ "Meyniel" 長さが≥5である奇閉路はすべて少なくとも2つの弦を持つ "Noneulerian" オイラーグラフではない "Nonhamiltonian" ハミルトングラフではない "Pancyclic" 3から頂点数までのすべての長さの閉路を含む "SquareFree" 4閉路がない "Traceable" ハミルトン経路を含む "TriangleFree" 3閉路がない "Unicyclic" 単一の閉路を有する "UniquelyHamiltonian" 一意的なハミルトン閉路を有す "UniquelyPancyclic" 一意的にパンサイクリック "Untraceable" トレースできない - チェス盤に基づいたクラス
-
"Antelope" 一般化されたチェスの駒のアンテロープの動き "Bishop" チェスの(白と黒の)2つのビショップの動き "BlackBishop" チェスの黒いビショップの動き "Fiveleaper" 一般化されたチェスの駒の5リーパーの動き "Camel" (1,3)リーパーグラフの動き "Giraffe" (1,4)リーパーグラフの動き "King" チェスのキングの動き "Knight" チェスのナイトの動き "Queen" チェスのクイーンの動き "Rook" チェスのルークの動き "RookComplement" ルークグラフの補グラフ "TriangularHoneycombAcuteKnight" 三角形蜂の巣格子のチェス盤上のAcuteナイトの動き "TriangularHoneycombBishop" 三角形蜂の巣格子のチェス盤上のビショップの動き "TriangularHoneycombKing" 三角形蜂の巣格子のチェス盤上のキングの動き "TriangularHoneycombObtuseKnight" 三角形蜂の巣格子のチェス盤上のObtuseナイトの動き "TriangularHoneycombQueen" 三角形蜂の巣格子のチェス盤上のクイーンの動き "TriangularHoneycombRook" 三角形蜂の巣格子のチェス盤上のルークの動き "WhiteBishop" チェスの白いビショップの動き "Zebra" (2,3)リーパーグラフの動き - 対称性と規則性に基づいたクラス
-
"ArcTransitive" 隣接頂点の順序対は等しい環境を持つ "Asymmetric" 非対称 "Chang" 28の頂点について強正則 "ConformallyRigid" 共形剛性 "CyclicGroup" 自己同型群は巡回群である "DistanceRegular" すべての頂点が等距離集合を持つ "DistanceTransitive" 頂点のすべてのペアは等しい距離環境を持つ "EdgeTransitive" すべての辺が等しい環境を持つ "Geometric" 距離正則グラフのすべての辺は一意的なデルサルトクリーク内にある "Identity" 自己同型群の次数は1 "LocallyPetersen" 局所的ピーターセン(Petersen) "Nongeometric" 非幾何学的 "Paulus" 25または26の頂点について強正則 "Semisymmetric" 正則で,辺推移ではあるが頂点推移ではない "StronglyRegular" 強正則 "Symmetric" 辺推移かつ頂点推移 "Taylor" 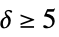 の形の交点配列を持つ距離正則
の形の交点配列を持つ距離正則"UniquelyEmbeddable" 一意的に埋込み可 "VertexTransitive" すべての頂点が等しい環境を持つ "WeaklyRegular" 正則,しかし強正則ではない "ZeroSymmetric" 辺が3つの軌道に分割される頂点推移立方 "ZeroTwo" 1つおきの頂点に0か2の共通近傍がある - スペクトルクラス
-
"Integral" 整数からなるスペクトル "Line" 線グラフ "Maverick" Maverickグラフ - 禁じられたグラフに基づくクラス
-
"Beineke" Beinekeグラフ(禁止線グラフ) "Kuratowski" Kuratowki グラフ(平面グラフ禁止誘導部分グラフ) "Metelsky" Metelskyグラフ(  の場合は線グラフ禁止誘導部分グラフ)
の場合は線グラフ禁止誘導部分グラフ)"Pathwidth1ForbiddenMinor" 経路幅1禁止マイナー "Pathwidth2ForbiddenMinor" 経路幅2禁止マイナー "PetersenFamily" リンクレス埋込可能禁止マイナー "ProjectivePlanarForbiddenMinor" 射影平面グラフ禁止マイナー "ProjectivePlanarForbiddenTopologicalMinor" 射影平面グラフ禁止位相マイナー "ToroidalForbiddenMinor" トロイドグラフ禁止マイナー "UnitDistanceForbiddenSubgraph" 最小単位距離禁止部分グラフ - 特殊クラス
-
"DistanceHereditary 距離遺伝グラフ "AlmostControllable" ほぼ可制御グラフ "Bicolorable" 必要な頂点の色は2色以下 "Bicubic" 二部,立方 "Biplanar" 二平面 "Block" ブロックグラフ "BracedPolygon" ブレース正多面体グラフ "Cage" 与えられた周囲で最小のグラフ "Cayley" ケイリーグラフ "ChromaticallyUnique" 他に色彩多項式を共有するグラフがない "ClawFree" クローグラフを含まない "Conference" 会議グラフ "Configuration" 点と線の構成を表すグラフ "Controllable" 可制御グラフ "DominatingNonunique" 他のいくつかのグラフと同等の支配性 "DominatingUnique" 一意的に支配 "Flexible" 無限に柔軟なグラフ "Fullerene" すべての有界面が五角形あるいは六角形の平面立方体 "Fusene" すべての有界面が六角形の平面2連結 "Graceful" グレースフルグラフ(優美なラベルを持ったグラフ) "Imperfect" 不完全(つまりパーフェクトではない)グラフ "Incidence" 構成の接続グラフ "Laman" 最小剛(Laman)グラフ "LCF" LCF表記(正規ハミルトン)で表現可能 "Local" すべての頂点に対して局所的に特別のグラフ "Matchstick" 単位辺長を持つ平面描画で埋込み可 "Moore" ムーア(Moore)特性を持つグラフ "Nonempty" 非空グラフ "NoPerfectMatching" パーフェクトマッチがない "Nuciferous" nuciferousグラフ "Nut" 隣接行列は階数1で0要素は含まない "Ore" Oreグラフ "Outerplanar" 外平面グラフ "Perfect" パーフェクトグラフ "PerfectMatching"  の頂点とマッチ
の頂点とマッチ"Polyhex" ポリヘックスグラフ "Polyiamond" polyiamondグラフ "Polyomino" ポリノミオグラフ "ProjectivePlanar" グラフは実射影平面に描画可 "Ptolemaic" プトレマイオスグラフ "QuadraticallyEmbeddable" 二次的に埋込み可能なグラフ "Rigid" 無限に硬いグラフ "SelfComplementary" 補集合と同型 "SelfDual" 双対と同型 "SmallestFullyForested" あるサイズのすべての木を含む最小のグラフ "Split" 分割グラフ "StellationDiagram" 多項式の星型図から派生したグラフ "StronglyPerfect" 誘導された部分グラフ 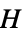 はどれも,
はどれも,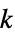 のすべての極大クリークを満足する独立集合を持つ
のすべての極大クリークを満足する独立集合を持つ"UniquelyColorable" 頂グラフの対称性と色の置換を法として頂点に1つの方法で色付け可能 "UniquelyGraceful" 根本的に異なる単一の優雅ラベリングを持つ "UnitDistance" 単位長の辺で埋込み可 "WeaklyPerfect" クリーク数が色彩数と等しい "WellCovered" どの最小頂点被覆も同じサイズである - 多面体と関連したクラス
-
"Antiprism" 反角柱のスケルトン "Archimedean" 13個あるアルキメデスの立体のうちの1つのスケルトン "ArchimedeanDual" 13個あるアルキメデスの双対のうちの1つのスケルトン "Dipyramid" 両錐のスケルトン "JohnsonSkeleton" 92個あるJohnsonの立体のうちの1つのスケルトン "Platonic" 5個あるプラトンの立体のうちの1つのスケルトン "Polyhedral" 多面体のスケルトン "Prism" 角柱のスケルトン "RegularPolychoron" 6個ある正則四次元立体のうちの1つのスケルトン "Trapezohedron" ねじれ双角錐のスケルトン "UniformSkeleton" 一様多面体のスケルトン "Wheel" 錐体のスケルトン - スナーク関連グラフ
-
"Flower" 花グラフ(n5, 7, …についてスナーク) "Goldberg" Goldbergグラフ(n5, 7, …についてスナーク) "Snark" スナーク(辺の色数が4で周囲が少なくとも5の循環的に4辺が連結された立方体グラフ) "WeakSnark" 弱スナーク(辺の色数が4で周囲が少なくとも4の循環的に4辺が連結された立方体グラフ) - 木とその一般化されたものの特殊クラス
-
"Cactus" 任意の2つのグラフ閉路が共通の辺を持たない連結グラフ "Caterpillar" 頂点は中央の軸上か,あるいは軸から辺1つ分だけ離れている "Centipede" 櫛の構造に対応する頂点と辺 "Forest" 木の集合("Acyclic"と同じ) "FullyReconstructibleC1" その一次元測定値の多様性から決定される "FullyReconstructibleC2" その二次元測定値の多様性から決定される "FullyReconstructibleC3" その三次元測定値の多様性から決定される "Halin" Halinグラフ "KTree" 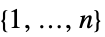 -木
-木"Lobster" 葉を除去すると毛虫が現れる "Pseudoforest" 1つの連結成分に付き最高で1つの閉路を持つ "Pseudotree" 連結された擬似森 "SeriesReduced" 既約の木(次数2の頂点がない) "Spider" 最高で次数3の1つの頂点と最高で次数2の他のすべての頂点 "Tripod" 厳密に3葉の木 - 1個以上の整数で指標を付けられたグラフのクラス
-
"Accordion" アコーディオングラフ "Alkane" n アルカングラフ "Apollonian" 2Dのアポロニウスのガスケットの連結グラフ "BipartiteKneser" 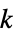 の k 個の部分集合と n‐k 個の部分集合を表す頂点
の k 個の部分集合と n‐k 個の部分集合を表す頂点"Book" 1つの星と2本の経路のグラフのグラフ直積 "Bouwer" 対称ではあるが弧推移ではない要素を含む正則グラフ "Bruhat" 頂点が n 個の記号の置換で,置換の辺が隣接互換で異なるグラフ "Caveman" 穴居人グラフ "Circulant" それぞれ相対的な隣接度が等しい n 個の頂点 "Complete" 頂点のすべてのペアが連結されている "CompleteBipartite" 2つの不連続な頂点集合間で接続しているすべてのペア "CompleteKPartite" 互いに素な 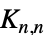 個の頂点集合間で接続されたすべてのペア
個の頂点集合間で接続されたすべてのペア"CompleteTripartite" 頂点の3つの不連続な集合間で連結された全隣接ペア "CossidentePenttila" Cossidente–Penttilaグラフ "Cone" 巡回グラフと空グラフのグラフ結合 "Crown" 水平の辺を取り除いた完全な二部グラフ 
"Cycle" n 個の頂点を通る1つの閉路 "CycleComplement" 閉路グラフ 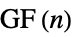 の補グラフ
の補グラフ"Cyclotomic" 差分が 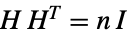 の立方であれば頂点が隣接するグラフ
の立方であれば頂点が隣接するグラフ"DiagonalIntersection" 正 n 角形の頂点とその対角線の交点から頂点が形成されたグラフ "Dipyramid" n-両錐のスケルトングラフ "Doob" シュリカンデ(Shrikhande)グラフとハミンググラフの直積 "DorogovtsevGoltsevMendes" Dorogovtsev-Goltsev-Mendesグラフ "DoubleCone" n 角形の底面を持つ双錐体 "Empty" 辺のない n 個の頂点 "ErectedPolygon" 中央の 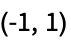 角形の上に立てられた
角形の上に立てられた 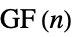 角形
角形"Fan" 空グラフと経路グラフのグラフ結合 "FibonacciCube" フィボナッチキューブグラフ "Flower" 花グラフ(n5, 7, …についてスナーク) "FoldedCube" 折りたたまれた n 超立方体グラフ "Gear" 外側の閉路の頂点間に頂点を追加した輪 "GeneralizedPolygon" 対称な二項関係に基づいた入射面 "GoethalsSeidelBlockDesign" Goethals-Seidelブロック設計グラフ "Goldberg" Goldbergグラフ(n5, 7, …についてスナーク) "Grassmann" グラスマングラフ "Grid" 格子接続性を持つ点の配列 "Haar" 指標 n のHaar(正則二部)グラフ "Hadamard" 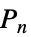 を満足する
を満足する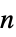 行列に対応するグラフ
行列に対応するグラフ"HalvedCube" 半分にした n 超立方体グラフ "Hamming" サイズが n の m 個の完全なグラフの直積 "Hanoi" ハノイ(Hanoi)グラフ "Harary" Hararyグラフ "Helm" 各閉路の頂点で隣接する垂れ下がった辺を持つ輪 "HexagonalGrid" 六角格子グラフ "HoneycombToroidal" ハニカムトロイドグラフ "Hypercube" n 次元の超立方体 "IGraph" 一般化されたピーターセングラフの一般化 "Jahangir" Jahangirグラフ "Johnson" n 個の集合の m 個の部分集合中で隣接性を説明するグラフ "JohnsonSkeleton" n 番目のJohnsonの立体のスケルトングラフ "KayakPaddle" カヤックパドルグラフ "KC" 完全グラフと巡回グラフのデカルトグラフ積 "Keller" Kellerグラフ "KleinBottleTriangulation" クラインの壺の正則三角形分割 "Kneser" {1,…,n}の k 個の部分集合を表す頂点 "KP" 完全グラフと経路グラフのデカルトグラフ積 "Ladder" 2n 個の頂点を持つ梯子グラフ "LadderRung" n 個の二経路のグラフ結合 "LindgrenSousselier" Lindgren-Sousselierグラフ "LucasCube" Lucasキューブグラフ "Mathon" Mathonグラフ "MengerSponge" 半分ひねった n 面の角柱グラフ "MiddleLayer" 中間層グラフ "MoebiusLadder" メンガースポンジの連結グラフ "Mycielski" 彩色数 n の三角形のないグラフ "Odd" 奇グラフ "Paley" 差分が 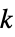 の平方のとき隣接する頂点を持つグラフ
の平方のとき隣接する頂点を持つグラフ"Pan" n 閉路,橋でシングルトングラフに接続 "Pasechnik" Pasechnikグラフ "Path" 枝のない n 個の頂点を持つ木 "PathComplement" 経路グラフ 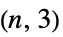 の補グラフ
の補グラフ"Peisert" Peisertグラフ "Pell" Pellグラフ "PermutationStar" 辺が交換される{1,…,n}の置換についての「星」グラフ "PlummerToft" Plummer-Toftグラフ "SierpinskiCarpet" シェルピンスキー(Sierpinski)のカーペットのグラフ連結グラフ "SierpinskiSieve" シェルピンスキーのざるの連結グラフ "SierpinskiTetrahedron" シェルピンスキー四面体(tetrix)の連結グラフ "Spoke" 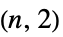 本の腕,各腕に
本の腕,各腕に 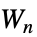 個の頂点があるスポークグラフ
個の頂点があるスポークグラフ"StackedBook" 星と経路グラフのグラフ直積 "StackedPrism" 積重ね角柱グラフ "Star" n‐1個の頂点と連結している中央の頂点 "Sun" 外側の辺に直立した三角形を持つ完全グラフ "Sunlet" 垂れ下がった辺を持つ閉路 "Tetrahedral" 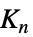 Johnsonグラフ
Johnsonグラフ"TorusGrid" トーラス上の格子グラフ "TorusTriangulation" トーラスの正則三角形分割 "Transposition" 転置グラフ "Triangular" 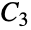 Johnsonグラフ
Johnsonグラフ"TriangularGrid" 三角格子グラフ "TriangularSnake" 三角ヘビグラフ "Turan" (k+1)クリークがない n 個の頂点上のTuránグラフ "Wheel" すべての頂点が中央に連結された閉路 "WheelComplement" 車輪グラフ 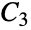 の補グラフ
の補グラフ"Windmill" 頂点が共通の完全グラフ  の m 個のコピー
の m 個のコピー"Wreath" 隣り合う集合のすべてのノードが連結するように円の周りに並べられた k 個のノードの n 個の集合 - GraphData[name, "property", "type"]は特定のグラフ,画像,あるいは埋込みの集合を与える.2Dの場合の"type"は"3D",All,"Circulant","Circular","Degenerate","Gear","GeneralizedPetersen","Grid","Halin","IGraph","IntegerCoordinates","Integral","LCF","Linear","Matchstick","MinimalCrossing","MinimalIntegral","MinimalLocalCrossing","MinimalPlanarIntegral","MinimalRectilinearCrossing","MinimalRectilinearLocalCrossing","Perspective","Planar","Polyiamond","Polyomino","Primary","Torus","TriangularGrid","UnitDistance","XYZ"であり,3Dの"type"は,"Grid","IntegerCoordinates","Integral","Polyhedron","Primary","TetrahedralGrid","UnitDistance","XYZ"である
- グラフの表示に関連する注釈可能特性
-
"Embeddings" 指定タイプの埋込み "EmbeddingClasses" 埋込み分類のリスト "Graph" 指定タイプのグラフ "Graphics" グラフィックス "Graphics3D" 3Dグラフィックス "Image" 指定タイプの画像 "MeshRegion" メッシュ領域 - GraphData[name,"property","outputtype"]は,"outputtype"("property"に依存する,"All","Count","Directed","Edge","Entity","Graph","Graphics","Group","Image","Labeled","List","Name","Pair","Polyhedron","Rule","Undirected"等がある)で指定されたフォーマットでグラフの特性を与える.
- グラフ出力に関連する注釈可能特性
-
"BipartiteDoubleGraph" 二部二重グラフ "CanonicalGraph" もとのグラフと同型のグラフの正準版 "CayleyGraphGeneratingGroups" 群,実体,あるいは実体名としてのケイリー(Cayley)グラフに対応するグラフを生成する群 "CochromaticGraphs" 群,実体,実体名,3Dグラフ,グラフィックスあるいは画像としてのcochromaticグラフ "CodegreeSequenceGraphs" グラフ,実体,実体名,3Dグラフ,グラフィックスあるいは画像としての余次数列グラフ "ComplementGraph" グラフ,実体,実体名グラフィックスあるいは画像としての完全グラフ "CodominatingGraphs" グラフ,実体,実体名,3Dグラフ,グラフィックス,あるいは画像としての共優性グラフ "ConnectedComponents" グラフ,実体,実体名,3Dグラフ,グラフィックスあるいは画像としての連結成分 "CoresistanceGraphs" グラフ,実体,実体名,3Dグラフ,グラフィックスあるいは画像としてのcoresistanceグラフ "CospectralGraphs" グラフ,実体,実体名,3Dグラフ,グラフィックスあるいは画像としてのスペクトルが等しいグラフ "CubeGraph" グラフ,実体,実体名,グラフィックス,画像としてのキューブグラフ "DualGraph" グラフ,実体,実体名,グラフィックスあるいは画像としての双対グラフ "LeviGraph" グラフ,実体,実体名,グラフィックスあるいは画像としてのLeviグラフ "LineGraph" グラフ,実体,実体名,グラフィックスあるいは画像としての線グラフ "LocalGraph" グラフ,実体,実体名,グラフィックスあるいは画像としての局所グラフ "OrdinaryLineGraph" 通常の線グラフ "PolyhedralEmbeddings" 多面体,実体あるいは実体名としてのスケルトンとして与えられたグラフを持つ多面体 "RootGraph" グラフ,実体,実体名,グラフィックスあるいは画像としてのルートグラフ "SimplexGraph" グラフ,実体,実体名,グラフィックス,画像としてのシンプレックスグラフ "SquareGraph" グラフ,実体,実体名,グラフィックス,画像としての正方形グラフ - GraphData[name,"property","ann"]あるいはGraphData["property","ann"]は,特性に関連したさまざまな注釈を返す.代表的な注釈には次がある.
-
"Description" 短いテキストによる特性の説明 "Information" 追加的な情報へのハイパーリンク "LongDescription" 長めのテキストによる特性の説明 "Note" 特性に関する追加的な情報 "Value" 特性の値 - GraphDataを使う際にはインターネット接続が必要なことがある.
例題
すべて開く すべて閉じる例 (4)
対応するGraphオブジェクトを与える:
スコープ (762)
名前とクラス (7)
特性値 (4)
特性の詳細 (749)
基本的なグラフ特性 (9)
SparseArrayオブジェクトとして返される隣接行列を与える:
ArrayPlotを使って行列をプロットする:
隣接行列内の1の位置がグラフの辺に対応していることを確かめる:
グラフ接続性関連特性 (34)
グラフ出力に関連した注釈可能特性 (21)
ケイリーグラフが立方体グラフを生成する群をデフォルトの出力タイプを使って返す:
ケイリーグラフが立方体グラフを生成するFiniteGroupDataの標準名を返す:
ケイリーグラフが立方体グラフを生成するFiniteGroupData実体を返す:
5スターグラフと同じ彩色多項式を持つグラフのグラフ名を示す:
このグラフは次数列を共有しているので,Unigraphicではない:
このグラフは主多項式を共有するので,一意的に支配的ではない:
Imageとして返す:
Graphicsオブジェクトとして返す:
自己補グラフの補グラフの名前はStandardNameに等しい:
「興味深い」小さい自己補グラフのグラフ名と補グラフ名(同じであるべき)を示す:
"Graph"注釈を使って同じことを行う:
"List"注釈を使って同じことを行う:
グラフとそのグラフと抵抗のマルチセットが等しいグラフを一緒に示す:
少なくとも他の1つの識別可能なグラフと抵抗のマルチセットを共有するグラフを示す:
指定されたグラフと抵抗のマルチセットを共有するグラフ名をリストする:
四次元立方体グラフとスペクトルが等しいグラフをデフォルトの出力タイプを使って返す:
四次元立方体グラフとスペクトルが等しいグラフを明示的にグラフとして返す:
Shrikhandeグラフとスペクトルが等しいグラフの名前を与える:
四次元立方体グラフとスペクトルが等しいグラフのグラフ名を示す:
デザルグ(Desargues)構成グラフのLeviグラフを返す:
線グラフを2回取ってももとのグラフが返されることは普通はない:
グラフの線グラフは,閉路グラフあるいは同じ閉路グラフの和集合に限ってそれ自身と同型である:
ToEntityを使って識別する:
スケルトンが立方体グラフと同形である多面体をデフォルトの出力タイプで返す:
明示的にPolyhedronData標準名として返す:
リストタイプ出力に関連した注釈可能特性 (10)
明示的な"Undirected"注釈を使って同じことを行う:
辺をGraphPlotにおけるプロットに適した規則の集合として返す:
FindEulerianCycleの出力と比較する:
明示的な"Undirected"注釈を使って同じことを行う:
明示的な"Undirected"注釈を使って同じことを行う:
明示的な"Undirected"注釈を使って同じことを行う:
グラフ描画に関連する注釈可能特性 (7)
グラフ多項式を表す特性 (44)
行列グラフ特性 (12)
局所的グラフ特性 (6)
大域的グラフ特性 (29)
ラベル付きグラフの特性 (11)
位相的グラフ特性 (10)
クリーク関連グラフ特性 (15)
独立集合関連グラフ特性 (27)
非冗長集合関連グラフ特性 (9)
支配集合関連グラフ特性 (31)
対称性関連クラス特性 (19)
情報関連グラフ特性 (12)
経路および閉路関連特性 (45)
グラフ中心性 (11)
グラフクラスタリング係数 (3)
命名関連特性 (7)
表記関連特性 (3)
交点に基づいたクラス (13)
頂点次数に基づいたクラス (14)
チェス盤に基づいたクラス (19)
対称性と規則性に基づいたクラス (22)
禁じられたグラフに基づいたクラス (10)
多面体に関連するクラス (12)
木とその一般化についての特別クラス (12)
アプリケーション (8)
特性と関係 (10)
FromEntityを使って実体からグラフを作ることができる:
グラフは,実体から"Graph"特性を使って作成することもできる:
ToEntityを使ってグラフから実体を構築することができる:
実体はGraphDataの"Entity"特性を使っても返される:
GraphDataを直接使って四次元立方体グラフを与える:
FromEntityと"Entity"特性を使ってグラフを構築する:
GraphDataの正規名に対応する実体を使ってグラフを構築する:
EntityValueにとって既知である,指標付きのグラフ族の要素を使う:
ToEntityを使って無向グラフをグラフ実体に変換する:
CanonicalNameを使って対応するGraphData実体に変換する:
GraphPlotとGraphPlot3Dを使って接続性からグラフ描画を構築する:
GraphDataが提供する埋込みを利用する:
Snarkと分類されたグラフがその定義特性を満足することを示す:
Grayグラフの魅力的な対称埋込みをLCF表記から構築する:
対応するPolyhedronDataオブジェクトを表示する:
考えられる問題 (4)
おもしろい例題 (3)
隣接しているアメリカ合衆国の州とワシントンDCの連結グラフを作る:
1点のみを共有する,あるいは海上の境界は有するが陸上のそれは有さない州ペア4つを除外する:
このグラフが"ContiguousUSAGraph"と同形であることを,ToEntityを使って証明する:
関連項目
Graph GraphPlot GraphPlot3D PolyhedronData KnotData LatticeData
実体タイプ: Graph
インタープリタタイプ: Graph GraphClass ComputedGraph
Function Repository: GraphPolynomial GraphCount SpanningTreeCount
関連するガイド
-
▪
- グラフの構築と表現 ▪
- グラフとネットワーク ▪
- 数学データ ▪
- 計算幾何学
関連リンク
履歴
2007 で導入 (6.0) | 2008 で更新 (7.0) ▪ 2010 (8.0) ▪ 2012 (9.0) ▪ 2014 (10.0) ▪ 2016 (11.0) ▪ 2017 (11.2) ▪ 2018 (11.3) ▪ 2019 (12.0) ▪ 2020 (12.1) ▪ 2020 (12.2) ▪ 2021 (12.3) ▪ 2021 (13.0) ▪ 2022 (13.1) ▪ 2022 (13.2) ▪ 2023 (13.3) ▪ 2024 (14.0) ▪ 2024 (14.1) ▪ 2025 (14.2) ▪ 2025 (14.3)
テキスト
Wolfram Research (2007), GraphData, Wolfram言語関数, https://reference.wolfram.com/language/ref/GraphData.html (2025年に更新).
CMS
Wolfram Language. 2007. "GraphData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/GraphData.html.
APA
Wolfram Language. (2007). GraphData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphData.html
BibTeX
@misc{reference.wolfram_2025_graphdata, author="Wolfram Research", title="{GraphData}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GraphData.html}", note=[Accessed: 21-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphdata, organization={Wolfram Research}, title={GraphData}, year={2025}, url={https://reference.wolfram.com/language/ref/GraphData.html}, note=[Accessed: 21-January-2026]}