-
参见
- 函 数
- Graph
- GraphPlot
- GraphPlot3D
- PolyhedronData
- KnotData
- LatticeData
-
- 实体类型
- Graph
-
- 诠释器类型
- Graph
- GraphClass
- ComputedGraph
- 相关指南
-
-
参见
- 函 数
- Graph
- GraphPlot
- GraphPlot3D
- PolyhedronData
- KnotData
- LatticeData
-
- 实体类型
- Graph
-
- 诠释器类型
- Graph
- GraphClass
- ComputedGraph
- 相关指南
-
参见


GraphData
更多信息









































- GraphData 中指定的 entity 可以是 Entity、实体列表或实体的标准名称,如 "PetersenGraph" 或 "FosterCage".
- GraphData[entity] 给出一个 Graph 对象.
- 指定的 property 可以是 EntityProperty、属性的标准名称或属性列表.
- GraphData[patt] 给出匹配字符模式 patt 的所有图名称列表.
- GraphData[] 列出所有标准的已定义的图.
- GraphData[All] 给出所有可能的图.
- GraphData[;;n] 给出含有 ≤n 个顶点的可用的标准的已命名图列表.
- GraphData[m;;n] 给出含有 m 到 n 个顶点的可用的标准的已命名图列表.
- GraphData[class,n] 等给出在指定 class 中带有 n 个顶点等的可用图列表.
- GraphData["Classes"] 给出所有支持类的列表.
- GraphData["Properties"] 给出图的可用属性的列表.
- GraphData[{n,i},…] 给出含有 n 个顶点的第 i 个简单图的数据.
- GraphData[{"type",id},…] 给出标识符 id 的指定 type 的图的数据. 标识符通常是一个整数或整数列表.
- 基本的图属性包括:
-
"AdjacencyMatrix" 邻接矩阵 "EdgeCount" 边的总数 "Edges" 边 "FaceCount" 面(平面图)的总数 "Faces" 面 "IncidenceMatrix" 关联矩阵 "VertexCount" 全部顶点数量 "Vertices" 顶点 - 和图的连通性有关的属性包括:
-
"AdjacencyLists" 邻接列表 "ArticulationVertexCount" 关节点的数量 "ArticulationVertices" 移除会使图不连通的顶点的列表 "BlockCount" 块 (block) 的数量 "Blocks" 最少 2-连通的分量 "BridgeCount" 桥的数目 "Bridges" 移除后会使图不连通的边的列表 "Connected" 连通 "ConnectedComponentCount" 连通分量的数量 "ConnectedInducedSubgraphCount" 连通的诱导子图数 "ConnectedComponents" 连通分量 "CyclicEdgeConnectivity" 循环边的连通性 "CyclicEdgeCutCount" 循环边割的数量 "CyclicEdgeCuts" 循环边割 "Degeneracy" 最大 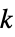 -核的大小
-核的大小"Density" 图中可能的边所占的比例 "Disconnected" 不连通 "EdgeConnectivity" 为了使图不连通删除的最少边数 "EdgeCutCount" 边割的数量 "EdgeCuts" 边割 (edge cuts) "IncidenceLines" 生成配置的共线顶点的索引 "LambdaComponents" lambda 分量 "LuccioSamiComponents" Luccio–Sami 分量 "MinimalEdgeCutCount" 极小边割的数量 "MinimalEdgeCuts" 极小边割 "MinimalVertexCutCount" 最小顶点割 (vertex-cut) 的数量 "MinimalVertexCuts" 最小顶点割 "MinimumCyclicEdgeCutCount" 最小循环边割数量 "MinimumCyclicEdgeCuts" 最小循环边割 "MinimumEdgeCutCount" 最小边割的计数 "MinimumEdgeCut" 最小边割 "MinimumVertexCutCount" 最小顶点割计数 "MinimumVertexCuts" 最小顶点割 "MinorCount" 图子式计数 "SpanningTrees" 生成树 "Strength" 图形强度 "Toughness" 图形韧度 "Triangulated" 三角化(最大平面) "VertexConnectivity" 为了使图不连通删除的最少点 - 与图子式 (graph minor) 有关的属性包括:
-
"HadwigerNumber" 哈德威格 (Hadwiger) 数 "MinorCount" 图子式计数 - 关于图显示的属性包括:
-
"EmbeddingClasses" 嵌入式类别标签列表,一个对应一种嵌入 "Embeddings" 所有可用布局的顶点坐标 "Graph" 图对象 "Graphics" 图形 "Graphics3D" 三维图形 "Image" 图像 "MeshRegion" 网格区域 "Polyhedron" 多面体 "VertexCoordinates" 默认布局的顶点坐标 - 与列表类型输出相关的可注释属性包括:
-
"AdjacencyMatrix","outputtype" 一个或全部邻接矩阵或所有可能的邻接矩阵数 "ConnectedComponents","outputtype" 以图形、列表、计数、边计数列表或顶点计数列表的形式连通分量 "Cycles","outputtype" 无向,有向,或环数 "Edges","outputtype" 作为列表、边列表、指数对列表、规则列表、图形或边数 "EulerianCycles","outputtype" 无向、有向,或欧拉环数 "Faces","outputtype" 作为列表的面、索引列表、图形,或面数 "HamiltonianCycles","outputtype" 无向、有向或哈密顿环数 "HamiltonianPaths","outputtype" 无向、有向或哈密顿路径数 "HamiltonianWalks","outputtype" 无向、有向或哈密顿行走数 "VertexCoordinates","outputtype" 一个或全部顶点坐标或嵌入数 "Vertices","outputtype" 作为列表、索引坐标规则列表、图形或顶点数的顶点 - 给出表示图多项式的纯函数的属性包括:
-
"CharacteristicPolynomial" 邻接矩阵的特征多项式 "ChordlessCyclePolynomial" 按长度编码无弦周期计数的多项式 "ChromaticPolynomial" 色多项式 "CliquePolynomial" 团多项式 "CoboundaryPolynomial" 共同边界多项式 "ComplementChordlessCyclePolynimial{ 按长度编码补图中的无弦环数的多项式 "ComplementOddChordlessCyclePolynomial" 按长度编码补图中的奇无弦环数的多项式 "ConnectedDominationPolynomial" 连通支配 (domination) 多项式 "ConnectedInducedSubgraphPolynomial" 按大小编码连通诱导子图数的多项式 "CyclePolynomial" 环多项式 "CyclicEdgeCutPolynomial" 循环边割多项式 "DetourPolynomial" 迂回矩阵的特征多项式 "DistancePolynomial" 距离多项式 "DominationPolynomial" 支配多项式 "EdgeCoverPolynomial" 边覆盖多项式 "EdgeCutPolynomial" 边割多项式 "FlowPolynomial" 流多项式 "IdiosyncraticPolynomial" Tutte 特殊多项式 "IndependencePolynomial" 独立多项式 "IrredundancePolynopmial" 无冗余多项式 "LaplacianPolynomial" 拉普拉斯多项式 "MatchingGeneratingPolynomial" 匹配生成多项式 "MatchingPolynomial" 匹配多项式 "MaximalCliquePolynomial" 按大小编码极大团数的多项式 "MaximalIndependencePolynomial" 按大小编码极大独立顶点集数的多项式 "MaximalIrredundancePolynomial" 按大小编码极大非冗余集数的多项式 "MaximalMatchingGeneratingPolynomial" 按大小编码极大独立边集数的多项式 "MinimalConnectedDominationPolynomial" 按大小编码极小连通支配集数的多项式 "MinimalDominationPolynomial" 按大小编码极小支配集数的多项式 "MinimalEdgeCoverPolynomial" 按大小编码极小边覆盖数的多项式 "MinimalEdgeCutPolynomial" 按大小编码极小边割数的多项式 "MinimalTotalDominationPolynomial" 按大小编码极小总支配集数的多项式 "MinimalVertexCoverPolynomial" 按大小编码极小顶点覆盖数的多项式 "MinimalVertexCutPolynomial" 按大小编码极小顶点割数的多项式 "OddChordlessCyclePolynomial" 按长度编码奇无弦环数的多项式 "PathPolynomial" 路径多项式 "QChromaticPolynomial" Q-色谱多项式 "RankPolynomial" 秩多项式 "ReliabilityPolynomial" 可靠性多项式 "SigmaPolynomial" 下降阶乘基的色多项式 "TotalDominationPolynomial" 按大小编码总支配集数的多项式 "TuttePolynomial" Tutte 多项式 "VertexCoverPolynomial" 顶点覆盖多项式 "VertexCutPolynomial" 按大小编码顶点割数的多项式 - 颜色相关的图属性包括:
-
"ChromaticInvariant" 色不变量 "ChromaticNumber" 色数 "ChromaticPolynomial" 色谱多项式 "ChromaticRoots" 色根 "CyclicChromaticNumber" 循环色数 "EdgeChromaticNumber" 边色数 "FractionalChromaticNumber" 分数色数 "FractionalEdgeChromaticNumber" 分数边色数 "MinimumVertexColoringCount" 最小顶点着色数 "MinimumVertexColorings" 最小顶点着色 "MinimumEdgeColoring" 最小边着色 "MinimumWeightFractionalColoring" 最小权值分数着色 "QChromaticPolynomial" Q-色谱多项式 "WeisfeilerLemanDimension" Weisfeiler–Leman 维度 - 图指数属性包括:
-
"ABCIndex" 原子-键连接性指数 "ArithmeticGeometricIndex" 算术几何指数 "BalabanIndex" Balaban 指数 "CircuitRank" 移除的最小边数变成非周期性 "DetourIndex" 迂回指数 "HararyIndex" Harary 指数 "HosoyaIndex" Hosoya 指数 "KirchhoffIndex" Kirchhoff 指数 "KirchhoffSumIndex" Kirchhoff 总和指数 "MolecularTopologicalIndex" 分子拓扑(第二 Schultz)指数 "RandicIndex" Randić 指数 "SomborIndex" Sombor 指数 "StabilityIndex" 稳定指数 "TopologicalIndex" 拓扑(第一 Schultz)指数 "WienerIndex" Wiener 指数 "WienerSumIndex" Wiener 总和指数 "ZagrebIndex1" 第一 Zagreb 指数 "ZagrebIndex2" 第二 Zagreb 指数 - 矩阵图的属性包括:
-
"ABCMatrix" 原子-键连接矩阵 "AdjacencyMatrix" 邻接矩阵 "ArithmeticGeometricMatrix" 算术几何矩阵 "DetourMatrix" 最长路径距离矩阵 "DistanceMatrix" 距离矩阵 "IncidenceMatrix" 入射矩阵 "LaplacianMatrix" 拉普拉斯矩阵 "MaximumFlowMatrix" 最大流矩阵 "MinimumCostFlowMatrix" 最小费用流矩阵 "NormalizedLaplacianMatrix" 归一化拉普拉斯矩阵 "RandicMatrix" Randić 矩阵 "ResistanceMatrix" 单位电阻边的顶点对之间的电阻 "SomborMatrix" Sombor 矩阵 - 局部图属性包括:
-
"ChordCount" 弦数 "Chords" 弦 "Curvatures" 曲率 "IsolatedPointCount" 孤立结点的数量 "IsolatedPoints" 0 度的顶点 "LeafCount" 叶顶点的数目 "Leaves" 1 度的顶点 - 全局图属性包括:
-
"Anarboricity" 其并集为初始图的边不相交无环子图的最大数目 "ApexCount" 顶点计数 "Apices" 移除会使图变成平面图的顶点的列表 "Arboricity" 其并集为初始图的边不相交无环子图的最小数目 "Center" 图离心率等于半径的顶点的指数 "Circumference" 图的周长 "Coarseness" 线不相交非平面子图的最大数目 "Corank" 边数数目减去顶点数目加上连通分量数目 "Degeneracy" 图的简并性 "DegreeSequence" 单调非递增的顺序中的顶点度 "DeterminedByResistance" 没有其它图共享相同的电阻多重集 "DeterminedBySpectrum" 没有其它图共享频谱 "Diameter" 图的直径 "Eccentricities" 各顶点离心率 "FractionalArboricity" 分数荫度 "IntersectionArray" 相交数组 "LinearArboricity" 线性荫度 "MaximumLeafNumber" 任意生成树中树叶的最大数 "MaximumVertexDegree" 最大顶点度 "MeanCurvature" 平均曲率 "MeanDistance" 顶点间平均距离 "MinimumLeafNumber" 任何生成树中最小的树叶数 "MinimumVertexDegree" 最小顶点度 "Periphery" 图离心率等于直径的顶点的指数 "Pseudoarboricity" 伪荫度 "QuadraticEmbeddingConstant" 二次嵌入常数 "Rank" 顶点数目减去连通分量数目 "RegularParameters" 描述顶点的共有邻居数量的参数 "Skewness" 移除结果为平面图的最小边数 "SpanningTreeCount" 生成树的数目 "StarArboricity" 星形荫度 "Thickness" 并集为原始图的平面子图的最小数目 "TreeNumber" 覆盖图的边的最小数量的树 "Triameter" 图的 triameter(广义图直径) "VertexDegrees" 顶点度 - 谱图特性包括
-
"ABCEnergy" 原子-键连接能 "ABCSpectralRadius" 原子-键连接光谱半径 "AlgebraicConnectivity" 拉普拉斯矩阵的第二最小特征值 "ArithmeticGeometricEnergy" 算术-几何能 "ArithmeticGeometricSpectralRadius" 算术几何频谱半径 "Energy" 图能 "LaplacianSpectralRadius" 拉普拉斯频谱半径 "LaplacianSpectralRatio" 拉普拉斯频谱比 "LaplacianSpectrum" 拉普拉斯矩阵的特征值 "RandicEnergy" Randić 能 "SomborEnergy" Sombor 能 "SomborSpectralRadius" Sombor 频谱半径 "SpectralRadius" 频谱半径 "Spectrum" 邻接矩阵的特征值 "SpectrumSignature" 邻接矩阵特征值统计表 - 有标号的图的属性包括:
-
"AverageDisorderNumber" 平均无序数 "DisorderNumber" 无序数 "ErdosSequence" Erdős 序列 "GracefulLabelingCount" 根本上不同的优美标号的数量 "GracefulLabelings" 根本上不同的优美标号 "IrregularityStrength" 不规则强度 "PinnacleSetCount" 顶点集(pinnacle sets)的数量 "PinnacleSets" 顶点集(pinnacle sets) "RadioLabelingCount" 根本上不同的最佳广播标号 (radio labeling) 的数量 "RadioLabelings" 根本上不同的最佳广播标号 "RadioNumber" 广播数 - 图形构造属性包括:
-
"AssemblyNumber" 组装数 "ConstructionNumber" 构造数 - 拓扑图属性包括:
-
"CrossingNumber" 嵌入图中的最小交叉 "Dimension" 图形维度 "Genus" 产生非边缘交叉嵌入的最小句柄数 "KleinBottleCrossingNumber" 克莱因瓶嵌入的最小交叉 "LocalCrossingNumber" 局部交叉(local crossing)数量 "MapNumber" 地图数量 "MetricDimension" 度量维度 "ProjectivePlaneCrossingNumber" 射影平面嵌入的最小交叉 "RectilinearCrossingNumber" 直线嵌入的最小交叉 "RectilinearLocalCrossingNumber" 直线局部交叉(rectilinear local crossing)数量 "ToroidalCrossingNumber" 环形嵌入的最小交叉 - 团相关属性包括:
-
"CliquePolynomial 团多项式 "Cliques 团 "BicliqueNumber" 双团数目 "BipartiteDimension" 二分图维度 "CliqueCount" 团的数目 "CliqueCoveringNumber" 覆盖整个顶点集所需的最大团的最小数目 "CliqueNumber" 最大团中的顶点数 "DelsarteCliqueCount" Delsarte 团的数量 "DelsarteCliques 距离正则图中达到 Delsarte 边界的团 "FractionalCliqueNumber" 分数团数目 "LowerCliqueNumber" 最小极大团的尺寸 "MaximalCliqueCount" 不同的极大团的数目 "MaximalCliquePolynomial" 编码最大团大小计数的多项式 "MaximalCliques" 极大团 "MaximumCliqueCount" 极大团的数目 "MaximumCliques" 最大团 "MinimumCoveringsByMaximalCliques" 通过最大团的最小覆盖 "MinimumCoveringsByMaximalCliquesCount" 通过最大团的最小覆盖数 "SimplexGraph" 单纯形图 - 覆盖相关属性包括:
-
"CliqueCoveringNumber" 覆盖顶点集所需要的的最大团的最小数 "EdgeCoverCount" 边覆盖的数目 "EdgeCoverNumber" 最小边覆盖的大小 "EdgeCoverPolynomial" 边覆盖多项式 "EdgeCovers" 边覆盖 "MinimalEdgeCoverCount" 极小边覆盖的数目 "MinimalEdgeCoverPolynomial" 编码最小边覆盖尺寸计数的多项式 "MinimalEdgeCovers" 极小边覆盖 "MinimalVertexCoverCount" 极小顶点覆盖的数目 "MinimalVertexCoverPolynomial" 编码最小顶点覆盖大小计数的多项式 "MinimalVertexCovers" 极小顶点覆盖 "MinimumCliqueCoveringCount" 最小团覆盖的数目 "MinimumCliqueCoverings" 最小团覆盖 "MinimumEdgeCoverCount" 最小边覆盖(匹配)的数目 "MinimumEdgeCovers" 最小边覆盖(匹配) "MinimumPathCoveringCount" 最小路径覆盖的数目 "MinimumPathCoverings" 最小路径覆盖 "MinimumVertexCoverCount" 最小顶点覆盖的数目 "MinimumVertexCovers" 最小顶点覆盖 "PathCoveringNumber" 路径覆盖的数目 "VertexCoverCount" 顶点覆盖的数目 "VertexCoverNumber" 最小顶点覆盖的大小 "VertexCoverPolynomial" 顶点覆盖多项式 - 独立集相关属性包括:
-
"BipartiteDimension" 二分图维度 "EdgeIndependenceNumber" 独立边集大小的计数 "FractionalIndependenceNumber" 部分独立数(fractional independence number) "IndependenceNumber" 最大独立顶点集的大小 "IndependencePolynomial" 独立多项式 "IndependenceRatio" 独立比值 "IndependentEdgeSetCount" 独立边集的数目 "IndependentEdgeSets" 独立边集 "IndependentVertexSetCount" 独立顶点集的数目 "IndependentVertexSets" 独立顶点集 "IntersectionNumber" 交集数目 "LowerIndependenceNumber" 最小的极大独立顶点集的大小 "LowerMatchingNumber" 最小的极大独立边集的大小 "MatchingGeneratingPolynomial" 匹配生成多项式 "MatchingNumber" 匹配生成多项式的度数 "MatchingPolynomial" 匹配生成多项式 "MaximalIndependencePolynomial" 按大小编码极大独立顶点集数的多项式 "MaximalIndependentEdgeSetCount" 极大独立边集(匹配)的数目 "MaximalIndependentEdgeSets" 极大独立边集(匹配) "MaximalIndependentVertexSetCount" 极大独立顶点集的数目 "MaximalIndependentVertexSets" 极大独立顶点集 "MaximalMatchingGeneratingPolynomial" 按大小编码极大独立边集数的多项式 "MaximumIndependentEdgeSetCount" 极大独立边集(匹配)的数目 "MaximumIndependentEdgeSets" 极大独立边集(匹配) "MaximumIndependentVertexSetCount" 极大独立顶点集的数目 "MaximumIndependentVertexSets" 极大独立顶点集 - 与无冗余集相关的属性包括:
-
"IrredundanceNumber" (下)无赘数 "IrredundancePolynomial" 无赘多项式 "IrredundantSetCount" 无冗余集的数目 "IrredundantSets" 无冗余集 "MaximalIrredundancePolynomial" 编码极大非冗余集大小计数的多项式 "MaximalIrredundantSetCount" 极大无冗余集的数目 "MaximalIrredundantSets" 极大无冗余集 "MaximumIrredundantSetCount" 最大无冗余集的数目 "MaximumIrredundantSets" 最大无冗余集 "UpperIrredundanceNumber" (上)无赘数 - 与支配集相关的属性包括:
-
"CodominatingGraphs" 共享支配多项式的图 "ConnectedDominatingSetCount" 连通的支配集数 "ConnectedDominatingSets" 连通的支配集 "ConnectedDominationNumber" 连通支配集可能的最少点数 (smallest possible size) "ConnectedDominationPolynomial" 编码连通支配集大小计数的多项式 "DomaticNumber" 图的控制划分中不相交支配集的最大数量 "DominatingSetCount" 支配集的数目 "DominatingSets" 支配集 "DominationNumber" 支配集的最小可能大小 "DominationPolynomial" 编码支配集大小计数的多项式 "DominationRoots" 支配多项式的根 "MinimalConnectedDominatingSetCount" 极小连通支配集的数目 "MinimalConnectedDominatingSets" 极小连通支配集 "MinimalConnectedDominationPolynomial" 编码极小连通支配集大小计数的多项式 "MinimalDominatingSetCount" 极小支配集的数目 "MinimalDominatingSets" 极小支配集 "MinimalDominationPolynomial" 编码极小支配集大小计数的多项式 "MinimalTotalDominatingSetCount" 极小总支配集数 "MinimalTotalDominatingSets" 极小总支配集 "MinimalTotalDominationPolynomial" 编码极小总支配集大小计数的多项式 "MinimumConnectedDominatingSetCount" 最小连通的支配集数 "MinimumConnectedDominatingSets" 最小连通的支配集 "MinimumDominatingSetCount" 最小支配集的数目 "MinimumDominatingSets" 最小支配集 "MinimumTotalDominatingSetCount" 极小总支配集数目 "MinimumTotalDominatingSets" 极小总支配集 "TotalDominatingSetCount" 总支配集数目 "TotalDominatingSets" 总支配集 "TotalDominationNumber" 最小可能的总支配集的大小 "TotalDominationPolynomial" 编码总支配集大小计数的多项式 "UpperDominationNumber" 最大的极大支配集的大小 - 对称性相关属性包括:
-
"ArcTransitivity" s-弧传递图的最大阶数 s "AutomorphismCount" 顶点同构群的阶 "AutomorphismGroup" 图同构置换群 "Automorphisms" 与图的自同构对应的排列的列表 "CanonicalPolyhedronDistinctEdgeLengthCount" 相应的正规多面体中不同边长的数目 "CayleyGraphGeneratingGroupNames" 生成凯莱图的群的名称 "CayleyGraphGeneratingGroups" 生成凯莱图的群 "DistinguishingNumber" 可区别的数目 "FixingNumber" 固定数目 "MinimumDistinguishingLabelingCount" 最小可区别标记的数目 "MinimumDistinguishingLabelings" 最小可区别标记 "PlanarEmbeddingCount" 平面嵌入数 "SymmetricallyDistinctFaceCount" 对称的不同面的数目 "SymmetricallyDistinctFaces" 对称的不同面表示的列表 "SymmetricallyDistinctVertexPairCount" 对称相异顶点对的数量 "SymmetricallyDistinctVertexPairSignature" 对称相异顶点对的签名 "SymmetricallyDistinctVertices" 对称的不同顶点表示的列表 "SymmetricallyDistinctVertexCount" 对称的不同顶点的数目 "SymmetricallyEquivalentFaces" 对称等价面的列表 "SymmetricallyEquivalentVertices" 对称等价顶点的列表 - 与信息相关的属性包括:
-
"Bandwidth" 图带宽 "BroadcastTime" 图形广播时间 "BroadcastTimes" 顶点广播时间列表 "BurningNumber" 刻录数 "CheegerConstant" Cheeger 常数 "Conductance" 图导率 "CoolingNumber" cooling 数 "Gonality" gonality 阶数 "Likelihood" 由随机数生成和相应的 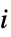 -子集选择的图的概率
-子集选择的图的概率"LovaszNumber" Lovász 数(香农容量的估计) "Pathwidth" 图页宽 "PebblingNumber" pebbling 数 "ScrambleNumber" scramble 数 "ShannonCapacity" 在图表示的交流模型中的有效字母表大小 "TreeDepth" 树深 "Treewidth" 图树宽 - 与路径和圈相关的属性包括:
-
"ChordlessCycleCount" 无弦环数 "ChordlessCyclePolynomial" 编码无弦环长度计数的多项式 "ChordlessCycles" 无弦环 "ComplementChordlessCycleCount" 图补中的无弦环数 "ComplementChordlessCyclePolynomial" 按长度计算的补图无弦环多项式编码符 "ComplementChordlessCycles" 图中长度至少为 4 的无弦环 "ComplementOddChordlessCycleCount" 补图的奇无弦环数 "ComplementOddChordlessCyclePolynomial" 编码补图的奇无弦环长度计数的多项式 "ComplementOddChordlessCycles" 补图的奇无弦环 "CubeGraph" 立方图 (graph cube) "CycleCount" 不同环的数目 "CyclePolynomial" 环多项式 "Cycles" 环列表 "EulerianCycleCount" 不同欧拉环的数目 "EulerianCycles" 欧拉环列表 "FaceSignature" 面长度的计数 "Girth" 最短环的长度 "HamiltonDecompositionCount" 哈密顿分解的数目 "HamiltonDecompositions" 边集到哈密顿环的划分 "HamiltonianCycleCount" 不同哈密顿环的数目 "HamiltonianCycles" 哈密顿环的列表 "HamiltonianNumber" 最短哈密顿行走的长度 "HamiltonianPathCount" 不同哈密顿路径的数目 "HamiltonianPaths" 哈密顿路径的列表 "HamiltonianWalkCount" 不同哈密顿行走的数目 "HamiltonianWalks" 哈密顿行走的列表 "HexagonCount" 6-环的数目 "KCyclicIndices" 标记图为第 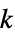 个
个 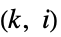 -环图的目录
-环图的目录 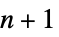
"LCFSignature" 所有可能 LCF 签名的阶数的计数 "LongestCycleCount" 最长环的数目 "LongestCycles" 最长环 "LongestPathCount" 最长路径数 "LongestPathLength" 最长路径长度 "LongestPaths" 最长路径 "MinimumPathCoveringCount" 最小路径覆盖的数目 "MinimumPathCoverings" 最小路径覆盖 "OddChordlessCycleCount" 奇无弦环数 "OddChordlessCyclePolynomial" 按长度编码奇无弦环数计数的多项式 "OddChordlessCycles" 奇数长度大於 3 的无弦环 "PathCount" 不同路径数 "PathCoveringNumber" 路径覆盖数目 "PathPolynomial" 路径多项式 "PathPolynomialMatrix" 路径多项式的矩阵函数 "Paths" 路径列表 "PentagonCount" 5-环数目 "Radius" 图半径 "SquareCount" 4-环数目 "SquareGraph" 方形图 (square graph) "TriangleCount" 3-环数目 - 图中心度包括:
-
"BetweennessCentralities" 中介中心度 "ClosenessCentralities" 紧密中心度 "DegreeCentralities" 顶点度 "EccentricityCentralities" 顶点离心率的倒数 "EdgeBetweennessCentralities" 边中介中心度 "EigenvectorCentralities" 特征向量中心度 "HITSCentralities" 中枢中心度 "KatzCentralities" Katz 中心度 "LinkRankCentralities" 链路排名中心度 "PageRankCentralities" 页面排名中心度 "RadialityCentralities" 径向中心度 "StatusCentralities" 状态中心度 - 图的集聚系数包括:
-
"GlobalClusteringCoefficient" 全局集聚系数 "LocalClusteringCoefficients" 局部集聚系数 "MeanClusteringCoefficient" 平均集聚系数 - 与名称相关的属性包括:
-
"AlternateNames" 英文替代名称 "AlternateStandardNames" 标准 Wolfram 语言替代名称 "Entity" 图实体 "Name" 英文名称 "Names" 英文名称及替代名称 "StandardName" 标准 Wolfram 语言名称 "StandardNames" 标准和替代 Wolfram 语言名称 - 与符号相关的属性包括:
-
"HouseOfGraphID" 图形库标识符 "LCFNotations" 基于哈密顿圈的嵌入式结构的图符号 "Notation" 用于图的主要的符号 "NotationRules" 用于指定图的符号的规则 "WikidataID" Wikidata 标识符 - GraphData["class"] 给出指定类中已定义的图列表. 根据图的名称 name 是否属于指定类,GraphData[name,"class"] 给出 True 或 False.
- GraphData[name,"Classes"] 给出图中对应于 name 的类的列表.
- 图的基本类别包括:
-
"Bipartite" 二分图 (被每条边连通的两个分量) "Nonplanar" 非平面的(需要交叉) "Nonsimple" 非简单图 "Planar" 平面的(无交叉) "Simple" 简单图(未标记的,无向的) "Tree" 树(无环) - 基于交叉的类别包括:
-
"Apex" 顶点图 "CriticalNonplanar" 非平面图,且去除任何一个顶点都会得到一个平面图 "Doublecross" 交叉数为 2 "DoubleToroidal" 亏格(genus)为 2 "IntrinsicallyLinked" 内在链路相连 "LinklesslyEmbeddable" 无链路可嵌入 "Map" 地图图 "NotUniquelyEmbeddable" 不可在球面上唯一嵌入 "Nonplanar" 交叉数 ≥ 1 "Planar" 交叉数为 0 "Pretzel" 亏格 (genus) 为 3 "Singlecross" 交叉数为 1 "Toroidal" 可在环状体上最小嵌入 "UniquelyEmbeddable" 在球面上可唯一嵌入 - 基于顶点度的类包括:
-
"Cubic" 每个顶点度为 3 "HighlyIrregular" 每个顶点周围都有不同的顶点度 "Multigraphic" 一个或多个其他图形有相同度序列 "Octic" 每个顶点度为 8 "Quartic" 每个顶点度为 4 "QuasiRegular" 每个顶点的度都相同,只有一个顶点的度比其他大一 "Quintic" 每个顶点度为 5 "Regular" 每个顶点的度相同 "Septic" 每个顶点度为 7 "Sextic" 每个顶点度为 6 "Switchable" 可以通过边的转换约化成另一个具有相同度序列的图 "TwoRegular" 每个顶点度为 2 "Unigraphic" 没有其他图与该度序列相同 "Unswitchable" 不可转换 - 基于遍历的类包括:
-
"Acyclic" 无环的 "AlmostHamiltonian" 哈密顿数为 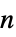 的
的 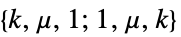 -节点图
-节点图"AlmostHypohamiltonian" 几近亚哈密顿的 (almost Hypohamiltonian) "Antipodal" 每个顶点正好有一个最大距离顶点 "Bridged" 含有至少一个桥 "Bridgeless" 没有桥 "Chordal" 没有无弦环 "Chordless" 无弦类 "Cyclic" 含有至少一个环 "Eulerian" 每条边仅包含一次的封闭环 "Geodetic" 在任何两个顶点之间有一条唯一的最短路径 "HamiltonConnected" 限制于一个哈密顿路的成对顶点 "HamiltonDecomposable" 其边集分割成哈密顿圈 "Hamiltonian" 每个顶点仅包含一次的封闭环 "HamiltonLaceable" 具有二分式端点的哈密顿连通图 "HStarConnected" 哈密顿连通或哈密顿定位的 "Hypohamiltonian" 移除一个顶点后是哈密顿图 "Hypotraceable" 移除一个顶点后是可追溯的图 "KempeCounterexample" 肯普四色算法的反例 "MaximallyNonhamiltonian" 最大非哈密顿的 "Median" 中值图 "Meyniel" 每一个长度 ≥5 的奇数周期至少有 2 条弦 "Noneulerian" 非欧拉的 "Nonhamiltonian" 非哈密顿的 "Pancyclic" 包含从 3 到顶点数的所有长度圈 "SquareFree" 不含 4-圈 "Traceable" 包含一条哈密顿路径 "TriangleFree" 不含 3-圈 "Unicyclic" 有一个单环 "UniquelyHamiltonian" 拥有唯一 Hamiltonian 周期 "UniquelyPancyclic" 唯一泛圈 "Untraceable" 不可追溯 - 基于棋盘的类包括:
-
"Antelope" 一枚广义羚羊棋子的移动 "Bishop" 两枚(白和黑)象的移动 "BlackBishop" 一枚黑象的移动 "Fiveleaper" 一枚广义五跳棋子的移动 "Camel" (1,3)-leaper 图形的移动 "Giraffe" (1,4)-leaper 图形的移动 "King" 一枚王的移动 "Knight" 一枚马的移动 "Queen" 一枚后的移动 "Rook" 一枚车的移动 "RookComplement" 车图的补图 "TriangularHoneycombAcuteKnight" 在一个三角蜂巢棋盘上移动一枚“锐角”马 "TriangularHoneycombBishop" 在一个三角蜂巢棋盘上移动一枚象 "TriangularHoneycombKing" 在一个三角蜂巢棋盘上移动一枚王 "TriangularHoneycombObtuseKnight" 在一个三角蜂巢棋盘上移动一枚“钝角”马 "TriangularHoneycombQueen" 在一个三角蜂巢棋盘上移动一枚后 "TriangularHoneycombRook" 在一个三角蜂巢棋盘上移动一个车 "WhiteBishop" 一枚白象的移动 "Zebra" (2,3)-leaper 图形的移动 - 基于对称和规律性的类包括:
-
"ArcTransitive" 具有相同环境的相邻顶点的有序对 "Asymmetric" 非对称 "Chang" 28 个顶点的强正规 "ConformallyRigid" 共形刚性 "CyclicGroup" 自同构群是循环的 "DistanceRegular" 所有顶点具有相同的距离 "DistanceTransitive" 所有顶点对具有相同距离环境 "EdgeTransitive" 所有边具有相同的环境 "Geometric" 距离正则图的每条边都位于唯一的 Delsarte 团中 "Identity" 相同次的自同构群 "LocallyPetersen" 局部 Petersen 图 "Nongeometric" 非几何 "Paulus" 25 或 26 个顶点的强正规 "Semisymmetric" 正规且边可传递,顶点不可传递 "StronglyRegular" 强正规 "Symmetric" 边和顶点都可传递 "Taylor" 正规于形式为 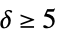 的交叉点数组的距离
的交叉点数组的距离"UniquelyEmbeddable" 唯一可嵌入 "VertexTransitive" 所有顶点具有相同的环境 "WeaklyRegular" 正规,但不强正规 "ZeroSymmetric" 边分割成三个轨道的顶点传递立方体 "ZeroTwo" 每两个顶点有 0 个或者 2 个共同的邻点 - 光谱等级包括:
-
"Integral" 频谱由整数组成 "Line" 线图 "Maverick" maverick 图 - 基于禁止图的类包括:
-
"Beineke" Beineke 图(如果是禁止的则不是线图) "Kuratowski" Kuratowki 图(禁止平面图) "Metelsky" Metelsky 图(如果是禁止的且 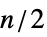 则不是线图)
则不是线图)"Pathwidth1ForbiddenMinor" 路径宽度 1 禁止子式 "Pathwidth2ForbiddenMinor" 路径宽度 2 禁止子式 "PetersenFamily" 无链路可嵌入的禁止子式 "ProjectivePlanarForbiddenMinor" 投影平面禁止子式 "ProjectivePlanarForbiddenTopologicalMinor" 投影平面禁止拓扑子式 "ToroidalForbiddenMinor" 禁止的环形图子式 "UnitDistanceForbiddenSubgraph" 禁止的最小单位距离 - 特殊类包括:
-
"DistanceHereditary 距离遗传图 "AlmostControllable" 基本可控图 (almost-controllable graph) "Bicolorable" 需要两种或更少的顶点色 "Bicubic" 二分图且是立方体图 "Biplanar" 双平面 "Block" 块状图 "BracedPolygon" 支撑 (braced) 正多边形图 "Cage" 给定周长的最小图 "Cayley" 凯莱图 "ChromaticallyUnique" 无其他图共享该色多项式 "ClawFree" 无爪图 "Conference" 会议图 "Configuration" 图形表示点线配置 "Controllable" 可控图 "DominatingNonunique" 支配多项式等价于其他图 "DominatingUnique" 支配多项式唯一 "Flexible" 无限灵活的图形 "Fullerene" 平面三度图且任意有界面都是五边形或六边形 "Fusene" 平面 2-连通图且所有有界面都是六边形 "Graceful" 优美图 "Imperfect" 不完美的图 "Incidence" 配置的关联图 "Laman" 最小刚性 (Laman) 图 "LCF" 用 LCF 符号描述(哈密顿立方) "Local" 对于所有顶点是一个局部特定图的图 "Matchstick" 可嵌入具有单位边长的平面图 "Moore" 带有 Moore 属性的图 "Nonempty" 非空图 "NoPerfectMatching" 没有完美匹配 "Nuciferous" Nuciferous 图 "Nut" 邻接矩阵的秩为 1 并不包含 0 元素 "Ore" Ore 图 "Outerplanar" 外平面图 "Perfect" 完美图 "PerfectMatching" 与 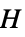 顶点匹配
顶点匹配"Polyhex" 多六隅图 "Polyiamond" 多正三角形图 "Polyomino" 多联骨牌图 "ProjectivePlanar" 可以在真实的投影平面上绘制图形 "Ptolemaic" Ptolemaic 图 "QuadraticallyEmbeddable" 二次可嵌入图形 "Rigid" 无限刚性图 "SelfComplementary" 同构于补图 "SelfDual" 同构于对偶图 "SmallestFullyForested" 包含所有一定大小的树的最小图 "Split" 分割图 "StellationDiagram" 从多面体的星状图导出的图 "StronglyPerfect" 每个导出子图 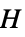 都有一个满足
都有一个满足 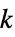 的所有极大团的独立集
的所有极大团的独立集"UniquelyColorable" 可通过单一方式对顶点进行着色,并对图形对称性和颜色的排列进行修改 "UniquelyGraceful" 拥有一个截然不同的优美标注 "UnitDistance" 可嵌入的单位长度的边 "WeaklyPerfect" 团数等于色数 "WellCovered" 每个极小顶点覆盖有相同的大小 - 与多面体相关的类包括:
-
"Antiprism" 反棱柱的框架 "Archimedean" 13 个阿基米德立体之一的框架 "ArchimedeanDual" 13 个阿基米德对偶之一的框架 "Dipyramid" 双锥框架 "JohnsonSkeleton" 92 个 Johnson 固体之一的框架 "Platonic" 五个柏拉图立体之一的框架 "Polyhedral" 多面体的框架 "Prism" 棱柱的框架 "RegularPolychoron" 六个正规四维立体之一的框架 "Trapezohedron" 梯形体的框架 "UniformSkeleton" 均匀多面体骨架 "Wheel" 角锥框架 - 与 Snark 相关的种类包括:
-
"Flower" 花图 (n5, 7, … 时的 snark 图) "Goldberg" Goldberg 图 (n5, 7, …) "Snark" snark 图(边色度为 4,周长至少为 5 的循环四边连通立方图) "WeakSnark" 弱 snark 图(边色度为4,且周长至少为 4 的循环四边连通立方图) - 树及其推广的特殊类包括:
-
"Cactus" 连通图,其中任意两个图圈没有共同的边 "Caterpillar" 顶点在树干的中心或只有一个边远离树干 "Centipede" 顶点和边成梳子状 "Forest" 树的集合(与 "Acyclic" 相同) "FullyReconstructibleC1" 根据其一维测量种类确定 "FullyReconstructibleC2" 根据其二维测量种类确定 "FullyReconstructibleC3" 根据其三维测量种类确定 "Halin" Halin 图 "KTree" 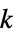 -树
-树"Lobster" 除去叶子得到毛虫状 "Pseudoforest" 每个连通分量至多包含一个圈 "Pseudotree" 连通伪森林 "SeriesReduced" 级数约简树图(没有顶点度为 2 的顶点) "Spider" 一个顶点度最多是3,其它顶点度最多是2 "Tripod" 恰好有三个叶子节点的树 - 用一个或多个整数标记的图的类型包括:
-
"Accordion" 手风琴图 "Alkane" n 烷烃图 "Apollonian" 二维 Apollonian 衬垫的连通图 "BipartiteKneser" 顶点表示 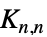 的 k 子集和 n-k 子集
的 k 子集和 n-k 子集"Book" 星状图和二路径图的笛卡尔乘积 "Bouwer" 包含对称但非弧传递的成员的正规图 "Bruhat" 图的顶点是 n 个符号上的置换,用于置换的边因相邻移项而不同 "Caveman" 穴居野人图 "Circulant" n 个顶点,相同的邻接方式 "Complete" 所有顶点对都相连 "CompleteBipartite" 所有连通对都横跨两个不相交的顶点集合 "CompleteKPartite" 所有连通对穿过 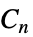 个不相交的顶点集
个不相交的顶点集"CompleteTripartite" 所有相邻对都横跨三个不相交的顶点集合 "CossidentePenttila" Cossidente–Penttila 图 "Cone" 圈图和空图的图连通 "Crown" 水平边被移除的完全二分 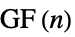
"Cycle" 穿过 n 个顶点的单环 "CycleComplement" 循环图 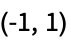 的补图
的补图"Cyclotomic" 带有相邻顶点的图,如果它们的差是 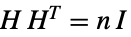 中的立方
中的立方"DiagonalIntersection" 由正 n-形的顶点及其对角线的交点形成顶点的图 "Dipyramid" n-双锥的框架图 "Doob" Shrikhande 图和 Hamming 图的笛卡尔乘积 "DorogovtsevGoltsevMendes" Dorogovtsev-Goltsev-Mendes 图 "DoubleCone" 以 n 角形为基点的双锥图 "Empty" 没有边的 n 个顶点 "ErectedPolygon" 在中心  边形上建立的
边形上建立的 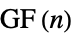 边形
边形"Fan" 带有路径图的空图的图连通 "FibonacciCube" Fibonacci 立方体图 "Flower" flower 图(n5, 7, … 的 snark 图) "FoldedCube" 折叠 n 超立方体图 "Gear" 外圈顶点之间附加顶点的轮图 "GeneralizedPolygon" 基于对称二元关系上的关联平面 "GoethalsSeidelBlockDesign" Goethals-Seidel 块状设计图 "Goldberg" Goldberg 图(n5, 7, … 的 snark 图) "Grassmann" Grassmann 图 "Grid" 有网格连通性的点的阵列 "Haar" 指数 n 的 Haar (普通二分)图 "Hadamard" 对应 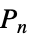 矩阵的图且满足
矩阵的图且满足 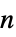
"HalvedCube" 对半的 n 超立方体图 "Hamming" 大小为 n 的 m 完全图的直积 "Hanoi" Hanoi 图 "Harary" Harary 图 "Helm" 在每个循环顶点处连通有吊坠边缘的轮图 "HexagonalGrid" 六角网格图 "HoneycombToroidal" 蜂巢环面图 "Hypercube" n 维超立方体 "IGraph" 广义 Petersen 图的推广 "Jahangir" Jahangir 图 "Johnson" 描述 n 集合的 m 个子集合间邻接关系的图 "JohnsonSkeleton" 第 n 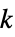 个 Johnson 固体的图框架
个 Johnson 固体的图框架"KayakPaddle" 皮划艇桨图 "KC" 完全图与循环图的笛卡尔图乘积 "Keller" Keller 图 "KleinBottleTriangulation" 克莱恩瓶的正三角划分 "Kneser" 表示 {1,…,n} 的 k 元素子集的顶点 "KP" 完全图与路径图的笛卡尔图乘积 "Ladder" 2n‐顶点的梯形图 "LadderRung" n 条二路径组成的图并集 "LindgrenSousselier" Lindgren-Sousselier 图 "LucasCube" Lucas 立方图 "Mathon" Mathon 图 "MengerSponge" 门格海绵的连通图 "MiddleLayer" 中间层图 "MoebiusLadder" 半螺旋状的 n 边棱柱图 "Mycielski" 色数 n 的无三角图 "Odd" 奇图 "Paley" 带有顶点相邻的图,如果它们的差是 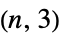 的平方
的平方"Pan" 由一个桥路连通到一个单点图的 n 圈 "Pasechnik" Pasechnik 图 "Path" 没有分支的 n 个顶点的树形图 "PathComplement" 路径图的互补图 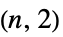
"Peisert" Peisert 图 "Pell" Pell 图 "PermutationStar" 边通过 {1 ,…,n} 的排列进行对换得到的星图 "PlummerToft" Plummer-Toft 图 "SierpinskiCarpet" Sierpiński 地毯的连通性图 "SierpinskiSieve" Sierpiński 筛子的连通性图 "SierpinskiTetrahedron" Sierpiński 四面体 (tetrix) 的连通图 "Spoke" 有 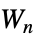 条臂,且每条臂上有
条臂,且每条臂上有 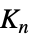 个顶点的辐条图 (spoke graph)
个顶点的辐条图 (spoke graph)"StackedBook" 星图和路径图的图笛卡尔乘积 "StackedPrism" 堆叠棱镜图 "Star" 中心顶点与 n-1 个顶点连通 "Sun" 外围边呈竖立三角的完全图 "Sunlet" 带有吊坠三角形的一个圈 "Tetrahedral" 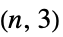 Johnson 图
Johnson 图"TorusGrid" 环面网格图 "TorusTriangulation" 圆环的正三角划分 "Transposition" 转置图 "Triangular" 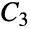 Johnson 图
Johnson 图"TriangularGrid" 三角网格图 "TriangularSnake" 三角蛇图 "Turan" 由 n 个顶点组成的 Turán 图,其中不含有 (k+1) 团 "Wheel" 所有顶点都与中心连通的一个圈 "WheelComplement" 轮状图的补图 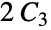
"Windmill" 带有一个共同顶点的完全图 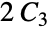 的 m 个副本
的 m 个副本"Wreath" n 个围绕圆圈排列的 k 个节点的集合,使得相邻集合中的所有节点都相连 - GraphData[name,"property","type"] 给出一组指定的图、图像或者嵌入结构,其中在二维空间内 "type" 可以包括 "3D", All、"Circulant"、"Circular"、"Degenerate"、"Gear"、"GeneralizedPetersen"、"Grid"、"Halin"、"IGraph"、"IntegerCoordinates"、"Integral"、"LCF"、"Linear"、"Matchstick"、"MinimalCrossing"、"MinimalIntegral"、"MinimalLocalCrossing"、"MinimalRectilinearLocalCrossing"、"MinimalPlanarIntegral"、 "MinimalRectilinearCrossing" 、"Perspective"、"Planar"、"Polyiamond"、"Polyomino"、"Primary"、"Torus"、"TriangularGrid"、"UnitDistance" 和 "XYZ";在三维空间内,"type" 可以包括 "Grid"、"IntegerCoordinates"、"Integral"、"Polyhedron"、"Primary"、"TetrahedralGrid"、"UnitDistance" 和 "XYZ".
- 与图显示相关的可注释属性包括:
-
"Embeddings","type" 具有某给定类型的嵌入式结构 "EmbeddingClasses","type" 嵌套分类列表 "Graph","type" 给定类型的图 "Graphics","type" 图形 "Graphics3D","type" 三维图形 "Image","type" 给定类型的图 "MeshRegion" 网格区域 - GraphData[name,"property","outputtype"] 给出由 "outputtype" 指定的格式的图属性,取决于 "property",这个属性可以是 "All"、"Count"、"Directed"、"Edge"、"Entity"、"Graph"、"Graphics"、"Group"、"Image"、"Labeled"、"List"、"Name"、"Pair"、"Polyhedron"、"Rule" 或 "Undirected".
- 与图输出相关的可注释属性包括:
-
"BipartiteDoubleGraph" 二分双图 (bipartite double graph) "CanonicalGraph" 与原始图同构的图的一般版本 "CayleyGraphGeneratingGroups" 生成凯莱图的群组 "CochromaticGraphs" 共色图 "CodegreeSequenceGraphs" 将序列图编码为图形、实体、实体名称、三维图形、图形或图像 "ComplementGraph" 补图 "CodominatingGraphs" 用图、实体、实体名称、3D 图、图形或图像给出的共支配图 "ConnectedComponents" 连通分量 "CoresistanceGraphs" 共电阻图 "CospectralGraphs" 同谱图 "CubeGraph" 作为图形、实体、实体名称、图形或图像的立方图 "DualGraph" 对偶图 "LeviGraph" 作为图形、实体、实体名称、图形或图像的 Levi 图 "LineGraph" 线图 "LocalGraph" 局部图 "OrdinaryLineGraph" 普通线图 "PolyhedralEmbeddings" 以给定图为骨架的多面体 "RootGraph" 将根图形作为图形、实体、实体名称、图形或图像 "SimplexGraph" 作为图形、实体、实体名称、图形或图像的单纯形图 "SquareGraph" 作为图形、实体、实体名称、图形或图像的方形图 - GraphData[name,"property","ann"] 或 GraphData["property","ann"] 给出关于属性的多个注解. 典型的注解包括:
-
"Description" 用较短文字描述特性 "Information" 附加信息的超链接 "LongDescription" 用较长文字描述特性 "Note" 特性的附加信息 "Value" 属性的数值 - 使用 GraphData 可能需要网络连通.
范例
打开所有单元 关闭所有单元基本范例 (4)
给出相应的 Graph 对象:
范围 (762)
名称和类 (7)
属性值 (4)
详细属性 (749)
基本的图属性 (9)
给出相邻矩阵,返回一个 SparseArray 对象:
用 ArrayPlot 绘制矩阵:
有关图连通的属性 (34)
和图显示有关的属性 (12)
与图输出相关的可注释的属性 (21)
返回其凯莱图可生成立方体图的 FiniteGroupData 标准名:
返回其凯莱图可生成立方体图的 FiniteGroupData 实体:
作为 Image 返回:
作为 Graphics 对象返回:
使用 "Graph" 注释做同样的运算:
使用 "List" 做同样的运算:
使用 ToEntity 进行识别:
显式返回 PolyhedronData 标准名称:
与列表类型输出相关的可注释的属性 (10)
将边作为一组规则返回,适用于在 GraphPlot 中绘图:
与 FindEulerianCycle 的输出相比:
与图显示相关的注解 (7)
返回图的所有表格式 Polyhedron 嵌入:
表示图多项式的属性 (44)
矩阵图的属性 (12)
给出邻接矩阵,以 SparseArray 对象的形式返回:
使用 ArrayPlot 绘制矩阵:
局部图属性 (6)
谱图属性 (13)
有标号的图的属性 (11)
覆盖相关的图属性 (20)
与无冗余集相关的图的属性 (9)
信息相关的图的属性 (12)
图的中心度 (11)
图的的集聚系数 (3)
与命名相关的属性 (7)
与记号相关的属性 (3)
基于交叉的类别 (13)
基于顶点度的类别 (14)
基于遍历的分类 (32)
基于国际象棋棋盘的类别 (19)
基于对称和正则性的类别 (22)
基于禁止图的类别 (10)
特殊类 (55)
与多面体相关的类别 (12)
用一个或多个整数索引的类别 (94)
应用 (8)
属性和关系 (10)
FromEntity 可用于从实体中生成图:
ToEntity 可用于从图构建一个实体:
通过 GraphData "Entity" 属性还可返回实体:
直接用 GraphData 给出超立方体图:
用 FromEntity 和 "Entity" 属性构建一个图:
用对应 GraphData 典型名称实体来构建图:
用 EntityValue 已知的索引图族构建:
用 ToEntity 转化无向图为图实体:
用 CanonicalName 转化为相应的 GraphData 实体:
用 GraphPlot 和 GraphPlot3D 根据连通性绘制图:
使用 GraphData 提供的嵌入:
显示相应的 PolyhedronData 对象:
可能存在的问题 (4)
巧妙范例 (3)
用 ToEntity 验证这个图与 "ContiguousUSAGraph" 同构:
参见
Graph GraphPlot GraphPlot3D PolyhedronData KnotData LatticeData
实体类型: Graph
诠释器类型: Graph GraphClass ComputedGraph
Function Repository: GraphPolynomial GraphCount SpanningTreeCount
相关链接
历史
2007年引入 (6.0) | 在以下年份被更新:2008 (7.0) ▪ 2010 (8.0) ▪ 2012 (9.0) ▪ 2014 (10.0) ▪ 2016 (11.0) ▪ 2017 (11.2) ▪ 2018 (11.3) ▪ 2019 (12.0) ▪ 2020 (12.1) ▪ 2020 (12.2) ▪ 2021 (12.3) ▪ 2021 (13.0) ▪ 2022 (13.1) ▪ 2022 (13.2) ▪ 2023 (13.3) ▪ 2024 (14.0) ▪ 2024 (14.1) ▪ 2025 (14.2) ▪ 2025 (14.3)
文本
Wolfram Research (2007),GraphData,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GraphData.html (更新于 2025 年).
CMS
Wolfram 语言. 2007. "GraphData." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2025. https://reference.wolfram.com/language/ref/GraphData.html.
APA
Wolfram 语言. (2007). GraphData. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphData.html 年
BibTeX
@misc{reference.wolfram_2025_graphdata, author="Wolfram Research", title="{GraphData}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GraphData.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_graphdata, organization={Wolfram Research}, title={GraphData}, year={2025}, url={https://reference.wolfram.com/language/ref/GraphData.html}, note=[Accessed: 09-March-2026]}