LinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]
連続する xiの値に対して yiをフィットする ![]() の形の線形モデルを構築する.
の形の線形モデルを構築する.
LinearModelFit[data,{f1,f2,…},{x1,x2,…}]
fiが変数 xkに依存する線形モデルを構築する.
LinearModelFit[{m,v}]
計画行列 m と応答ベクトル v から線形モデルを構築する.




LinearModelFit
LinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]
連続する xiの値に対して yiをフィットする ![]() の形の線形モデルを構築する.
の形の線形モデルを構築する.
LinearModelFit[data,{f1,f2,…},{x1,x2,…}]
fiが変数 xkに依存する線形モデルを構築する.
LinearModelFit[{m,v}]
計画行列 m と応答ベクトル v から線形モデルを構築する.
詳細とオプション










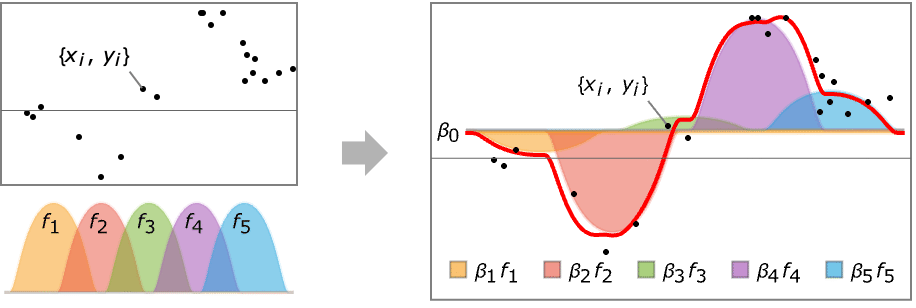
- LinearModelFitは,関数の線形結合を使って入力データをモデル化しようとする.
- LinearModelFitは,もとの
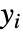 が平均
が平均 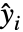 で共通標準偏差を持つ独立正規分布に従うという仮定の下に,
で共通標準偏差を持つ独立正規分布に従うという仮定の下に,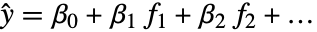 の形式の線形モデルを作成する.
の形式の線形モデルを作成する. - LinearModelFitは,構築する線形モデルを表す記号FittedModelオブジェクトを返す.
- 特定の点 x1, …におけるLinearModelFitからの最もよくフィットした関数の値は model[x1,…]で得ることができる.
- 次は,data の可能な形である.
-
{y1,y2,…} {{1,y1},{2,y2},…}という形式に等しい {{x11,x12,…,y1},…} 独立した値 xijと応答 yiのリスト {{x11,x12,…}y1,…} 入力値と応答の間の規則のリスト {{x11,x12,…},…}{y1,y2,…} 入力値と応答のリストの間の規則 {{x11,…,y1,…},…}n 行列の第 n 列をフィットする Tabular[…]name 表形式オブジェクト内の列 name をフィットする 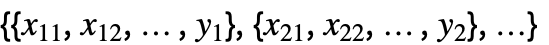 のような多変量のデータの場合,座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない.
のような多変量のデータの場合,座標 xi1, xi2, …の数は変数 xiの数と一致しなければならない.- データ点は近似実数でよい.不確かさはAroundを使って指定できる.
- さらに,data は,関数および変数を指定しなくても計画行列を使って指定できる.
-
{m,v} 計画行列 m と対応ベクトル v - LinearModelFit[{m,v }]の計画行列 m は,{{f1,f2,…},{f1,f2,…},…}形のデータ点における基底関数 fiの値によって形成される.応答ベクトル v は応答のリスト{y1,y2,…}である.
- 計画行列が使われるとき,基底関数 fiはLinearModelFit[{m,v},{f1,f2,…}]の形を使って指定できる.
- 計画行列 m と応答ベクトル v についてのモデルは
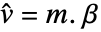 である.ここで,
である.ここで,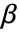 は推定すべきパラメータのベクトルである.
は推定すべきパラメータのベクトルである. - LinearModelFitで使用可能なオプション
-
ConfidenceLevel 95/100 母数と予測の信頼水準 IncludeConstantBasis True 定数基底関数を入れるかどうか LinearOffsetFunction None 線形予測器における既知のオフセット NominalVariables None 名義的あるいはカテゴリ的とみなされる変数 VarianceEstimatorFunction Automatic 誤差分散の推定のための関数 Weights Automatic データ要素の重み WorkingPrecision Automatic 内部計算で使う精度 - 設定をIncludeConstantBasis->Falseとすると,
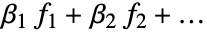 の形式のモデルがフィットされる.入力で計画行列が指定された場合は,オプションIncludeConstantBasisは無視される.
の形式のモデルがフィットされる.入力で計画行列が指定された場合は,オプションIncludeConstantBasisは無視される. - LinearOffsetFunction->h と設定すると,
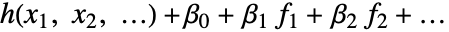 の形式のモデルがフィットされる.
の形式のモデルがフィットされる. - ConfidenceLevel->p のとき,確率 p の信頼区間は母数と予測区間に基づいて計算される.
- Weights->{w1,w2,…}と設定すると,yiの誤差分散は
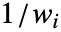 に比例すると考えられる.
に比例すると考えられる. - Weights->Automaticの設定でデータが厳密値を含んでいるときは,重みが1に設定される.データにAround値が含まれているなら,重みは
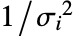 に設定される.ただし,
に設定される.ただし,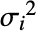 は応答分散の合計である.
は応答分散の合計である. - 応答分散の合計
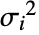 は,初期応答分散 si2と独立値の分散
は,初期応答分散 si2と独立値の分散 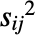 の関数である.
の関数である. -
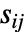 はAroundReplaceを使ってモデル内を伝播し,結果の分散が応答分散 si2に加えられる.関数FindRootを内部的に使ってFasanoおよびVioのメソッドに従った自己矛盾しない解が求められる.
はAroundReplaceを使ってモデル内を伝播し,結果の分散が応答分散 si2に加えられる.関数FindRootを内部的に使ってFasanoおよびVioのメソッドに従った自己矛盾しない解が求められる. - VarianceEstimatorFunction->f と設定すると,分散は f[res,w]で予測される.ただし res={y1-
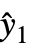 ,y2-
,y2-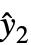 ,…}は剰余のリスト,w={w1,w2,…}は測定 yiの加重リストである.
,…}は剰余のリスト,w={w1,w2,…}は測定 yiの加重リストである. - VarianceEstimatorFunction->(1&)およびWeights->{1/Δy12,1/Δy22,…}を使うと,Δyiは測定yiの既知の不確実性として扱われ,母数標準誤差は事実上加重のみから計算される.
- FittedModelのデータと診断は model["property"]で得ることができる.
- データと model["property"]を使って得られたフィットされた関数に関連する特性
-
"BasisFunctions" 基底関数のリスト "BestFit" フィットされた関数 "BestFitAround" フィットされた関数と平均不確実性 "BestFitDataAround" フィットされた関数とデータの不確実性 "BestFitParameters" 母数推定 "Data" 入力データあるいは計画行列と応答ベクトル "DesignMatrix" モデルの計画行列 "Function" 最もよくフィットした純関数 "Response" 入力データの応答値 "Weights" データのフィットに使われる重み - 残差のタイプ
-
"FitResiduals" 実際の応答と予測された応答の差 "StandardizedResiduals" 各残差について標準誤差で割られたフィットの残差 "StudentizedResiduals" 単一の削除誤差推定で割られたフィットの残差 - 平方誤差の総和に関連する特性
-
"ANOVA" 分散データの解析 "CoefficientOfVariation" 応答平均で割られた推定標準偏差 "EstimatedVariance" 誤差分散の推定 "PartialSumOfSquares" 非定数基底関数が除去されるときのモデル平方和の変化 "SequentialSumOfSquares" 要素ごとに区切られたモデル平方和 - 母数推定の特性と診断
-
"CorrelationMatrix" 母数相関行列 "CovarianceMatrix" 母数共分散行列 "Eigenstructure" 母数相関行列の固有構造 "ParameterEstimates" フィットされた母数情報の表 "VarianceInflationFactors" 推定母数の拡大要因のリスト - 影響力の統計量関連特性
-
"BetaDifferences" 母数値の影響のDFBETAS尺度 "CatcherMatrix" キャッチャー行列 "CookDistances" クック(Cook)の距離のリスト "CovarianceRatios" 観察影響のCOVRATIO尺度 "DurbinWatsonD" 自己相関のDurbin–Watson 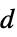 統計
統計"FitDifferences" 予測値に対する影響のDFFITS尺度 "FVarianceRatios" 観察影響のFVARATIO尺度 "HatDiagonal" ハット行列の対角要素 "SingleDeletionVariances" 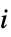 番目のデータ点を除いた分散推定のリスト
番目のデータ点を除いた分散推定のリスト - 予測値関連特性
-
"MeanPredictionBands" 平均予測の信頼帯 "MeanPredictions" 平均予測の信頼区間 "PredictedResponse" データのフィットされた値 "SinglePredictionBands" 1回の観察に基づいた信頼帯 "SinglePredictions" 1回の観察の予想される応答の信頼区間 - 適合度の尺度特性
-
"AdjustedRSquared" モデル母数の数に適応された 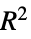
"AIC" 赤池情報量基準 "AICc" 有限サンプル修正AIC "BIC" ベイズ(Bayes)情報量基準 "RSquared" 決定係数 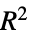
- 特性の"BestFit","BestFitAround","BestFitDataAround","BestFitDataAround"および"MeanPredictionBands"は,特定の独立した値でこれらの特k性を評価するために{"prop",x}または{"prop",{x1,x2,…}}として呼び出すこともできる.
- 特性"RSquared"と"AdjustedRSquared"については,平方和の合計の計算は,一定の基準が含まれている場合にのみ平均値補正される.
データ
オプション
特性
例題
すべて開く すべて閉じるスコープ (18)
データ (8)
モデル (3)
特性 (7)
データとフィットされた関数 (1)
影響力の統計量 (1)
予測値 (1)
オプション (11)
ConfidenceLevel (1)
LinearOffsetFunction (1)
データを既知のSqrt[x]項がある線形モデルにフィットする:
Weights (5)
Aroundの値を使ってデータ点に異なる重みを与える:
Aroundの値を独立変数と応答の両方に使う:
Aroundの値の複数の変数を持つモデルをフィットする:
FixedPointアルゴリズムを使ってモデルの重みを求めてみる:
減衰係数を小さくし,MaxIterationsを大きくすることで収束させる:
WorkingPrecision (1)
特性と関係 (10)
DesignMatrixはLinearModelFitで使われる計画行列を構築する:
デフォルトで,LinearModelFitとGeneralizedLinearModelFitは同じモデルをフィットする:
LinearModelFitは正規分布した誤差を想定して線形モデルをフィットする:
NonlinearModelFitは正規分布した誤差を想定して非線形モデルをフィットする:
FitとLinearModelFitは等しいモデルをフィットする:
LinearModelFitはフィットに関する追加的な情報を除去することを許す:
LeastSquaresを介して母数推定を得る:
LinearModelFitは線形モデルをフィットする:
FindFitは線形モデルおよび非線形モデルの母数推定を与える:
LinearModelFitは,TimeSeriesのタイムスタンプを変数として使う:
LinearModelFitは,複数の経路のあるTemporalDataについては,経路ごとに作用する:
テクニカルノート
-
▪
- 統計モデル解析
テキスト
Wolfram Research (2008), LinearModelFit, Wolfram言語関数, https://reference.wolfram.com/language/ref/LinearModelFit.html (2025年に更新).
CMS
Wolfram Language. 2008. "LinearModelFit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/LinearModelFit.html.
APA
Wolfram Language. (2008). LinearModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LinearModelFit.html
BibTeX
@misc{reference.wolfram_2025_linearmodelfit, author="Wolfram Research", title="{LinearModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/LinearModelFit.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_linearmodelfit, organization={Wolfram Research}, title={LinearModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/LinearModelFit.html}, note=[Accessed: 17-February-2026]}