MarginalDistribution

MarginalDistribution[dist,k]

多変量分布 dist の第 k 座標の一変量周辺分布を表す．

MarginalDistribution[dist,{k1,k2,…}]

第{k1,k2,…}座標の多変量周辺分布を表す．

詳細

  • 分布 dist は，多変量離散分布，多変量連続分布のどちらでもよい．
  • 確率密度関数が 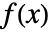の多変量離散分布 dist については，MarginalDistribution[dist,{k1,…,km}]の確率密度関数は 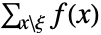で与えられる．ただし，ξ={xk1,…,xkm}である．
  • 確率密度関数が 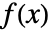の多変量連続分布 dist については，MarginalDistribution[dist,{k1,…,km}]の確率密度分布は 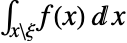で与えられる．ただし，ξ={xk1 ,…,xk m }である．
  • MarginalDistributionは，Mean，CDF，RandomVariate等の関数とともに用いることができる．

例題

すべて開くすべて閉じる

例  (3)

一次元周辺分布：

二次元周辺分布：

周辺分布は他の関数と同じように使うことができる：

スコープ  (34)

基本的な用法  (8)

第2座標の一変量周辺分布を求める：

多変量周辺分布は指定される座標順に依存する：

一変量周辺分布は一変量分布として振る舞う：

分布関数を求める：

多変量周辺分布は多変量分布のように振る舞う：

分布関数を求める：

各一変量周辺分布に対して特別なモーメントが計算される：

周辺分布のモーメントをもとの分布のモーメントと比較する：

一般的な多変量モーメントは境界モーメントからは求まらないことが多い：

一変量周辺分布の分位関数を計算することができる：

分位関数を求める：

あるいは特別な中央値を求める：

MarginalDistributionから確率変量を生成する：

ヒストグラムを周辺分布の確率密度関数のプロットと比較する：

分布母数を推定する：

三変量確率分布を定義する：

周辺分布を求める：

の共分散行列を求める：

周辺分布の分散は の共分散行列の対角を形成する：

パラメトリック分布  (2)

多くの多変量パラメトリック分布の周辺分布は自動的に簡約される：

一変量周辺分布はBetaDistributionに従う：

多変量周辺分布はDirichletDistributionに従う：

場合によっては，周辺分布が自動的に簡約されないこともある：

一変量周辺分布を簡約するとBinomialDistributionになる：

多変量周辺分布は簡約されない：

結果の周辺分布もまた他の分布と同じように使うことができる：

ノンパラメトリック分布  (3)

EmpiricalDistributionの周辺分布を求める：

周辺分布の累積分布関数：

SmoothKernelDistributionの周辺分布を求める：

HistogramDistributionの周辺分布を求める：

成分のヒストグラムと比較する：

派生分布  (9)

MarginalDistributionの周辺分布を求める：

の第2座標の周辺分布は の第3座標の周辺分布である：

CopulaDistributionの周辺分布を求める：

TruncatedDistributionの周辺分布を求める：

確率密度関数：

MixtureDistributionの周辺分布を求める：

各周辺分布が混合周辺分布である：

成分の周辺分布と比較する：

MixtureDistributionの周辺分布は周辺分布の混合分布である：

両周辺分布の確率密度関数をプロットする：

周辺分布を使って二変量分布を作成する：

もとの分布 の確率密度関数を周辺分布のProductDistributionと比較する：

共分散行列を比較する：

TransformedDistributionの周辺分布を求める：

ParameterMixtureDistributionの周辺分布を求める：

確率密度関数を可視化する：

OrderDistributionの周辺分布を求める：

確率密度関数：

平均：

分散：

QuantityDistributionの周辺分布はQuantityDistributionを与える：

一変量周辺分布：

多変量周辺分布：

自動簡約  (12)

離散パラメトリック分布  (3)

多変量DiscreteUniformDistributionの周辺分布も一様分布に従う：

MultivariatePoissonDistributionの一変量周辺分布はPoissonDistributionに従う：

多変量周辺分布も多変量ポアソン分布に従う：

MultinomialDistributionの一変量周辺分布はBinomialDistributionに従う：

連続パラメトリック分布  (6)

BinormalDistributionの周辺分布はNormalDistributionに従う：

MultinormalDistributionの一変量周辺分布はすべてNormalDistributionに従う：

MultinormalDistributionの多変量周辺分布は多変量正規分布に従う：

多変量UniformDistributionの周辺分布は一様分布に従う：

DirichletDistributionの一次元周辺分布はBetaDistributionに従う：

DirichletDistributionの多変量周辺分布もディリクレ分布に従う：

MultivariateTDistributionの一変量周辺分布はStudentTDistributionに従う：

LogMultinormalDistributionの一変量周辺分布はLogNormalDistributionに従う：

LogMultinormalDistributionの多変量周辺分布もまた対数多変量正規分布に従う：

派生分布  (3)

ProductDistributionの周辺分布は成分分布である：

一次元周辺分布：

二次元周辺分布もまたProductDistributionで定義される：

CopulaDistributionの一変量周辺分布は指定に使われた周辺分布である：

MixtureDistributionの周辺分布は成分の周辺分布の混合分布である：

アプリケーション  (5)

一変量周辺分布を二変量分布とともに可視化する：

一変量周辺分布を可視化する：

結果を共に示す：

中型車の市街地における単位燃料あたりの走行可能距離は二変量正規分布に従う．市街地の走行可能距離の分布を求める：

確率密度関数をプロットする：

市街地の平均走行可能距離を求める：

男性の体重と身長は二変量正規分布に従う．身長の分布を求める：

確率密度関数：

男性の身長の中央値を求める：

下位四分位点を求める：

身長の分布を単位を米にして表す：

3回続けて裏を出すことを目標に公正なコインを3回トスした．2回目または3回目に表が出たという形の失敗数の結合分布を求める：

確率密度関数：

それぞれの種類について平均失敗回数を求める：

両方の種類の失敗数の合計を求める：

2回目または3回目に表が出たことによる失敗数のシミュレーションを行う：

2つの都市 と に完全にキャンパスがまたがる大学がある．このキャンパスでは1日平均10件の交通事故が発生する．両方の都市の1日あたりの事故数を合わせた分布は次のようになる：

それぞれの都市の事故数の分布を求める：

確率密度関数を比較する：

都市 の1日あたりの事故数の30日間のシミュレーションを行う：

特性と関係  (5)

事象が変数すべてに依存しているわけではない場合は周辺分布を使う：

事象の確率を計算する：

関数がすべての変数を含んでいる訳ではない場合の期待値を求める：

個の変数を持つ多変量分布には個の適切な周辺分布がある：

補間変数の極限を取ることで周辺累積分布関数を求める：

周辺累積分布関数 を として計算する：

周辺累積分布関数 を として計算する：

補間変数上で積分することで周辺確率密度関数を得る：

周辺確率密度関数 を として計算する：

周辺確率密度関数 を として計算する：

多変量周辺分布には成分間の相関が保存されている：

第1，第3成分の周辺分布を求める：

周辺分布の共分散は部分行列である：

離散分布について：

の共分散行列：

第2，第3成分の周辺分布を定義する：

の共分散は の共分散の部分行列である：

おもしろい例題  (1)

三変量分布からの6つすべての適切な周辺確率密度関数：

Wolfram Research (2010), MarginalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MarginalDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), MarginalDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MarginalDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "MarginalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MarginalDistribution.html.

APA

Wolfram Language. (2010). MarginalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MarginalDistribution.html

BibTeX

@misc{reference.wolfram_2024_marginaldistribution, author="Wolfram Research", title="{MarginalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MarginalDistribution.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_marginaldistribution, organization={Wolfram Research}, title={MarginalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MarginalDistribution.html}, note=[Accessed: 17-November-2024 ]}