MarginalDistribution

MarginalDistribution[dist,k]

表示多变量分布 dist 中第 k 个坐标的单变量边缘分布.

MarginalDistribution[dist,{k1,k2,…}]

表示坐标 {k1,k2,…} 的多变量边缘分布.

更多信息

  • 分布 dist 可以为离散型或连续型多变量分布.
  • 对于概率密度函数为 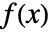的一个离散型多变量分布 dist，MarginalDistribution[dist,{k1,…,km}] 的概率密度函数由 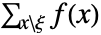给出，其中 ξ={xk1,…,xkm}.
  • 对于概率密度函数为 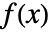的一个连续型多变量分布 dist，MarginalDistribution[dist,{k1,…,km}] 的概率密度函数由 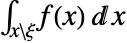给出，其中 ξ={xk1 ,…,xk m }.
  • MarginalDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.

范例

打开所有单元关闭所有单元

基本范例  (3)

一维边缘分布：

二维边缘分布：

边缘分布的使用方法与任何其它分布类似：

范围  (34)

基本用途  (8)

求第二个单变量边缘分布：

多变量边缘分布依赖于给定的坐标顺序：

单变量边缘分布的行为与单变量分布相同：

求分布函数：

多变量边缘分布的行为与多变量分布相同：

求分布函数：

对每个单变量边缘分布，计算特定的矩：

比较边缘分布的矩与原分布的矩：

从边缘矩中通常无法求得一个普通的多变量矩：

对单变量边缘分布可以计算分位数函数：

求分位数函数：

或者特定的中位数：

从 MarginalDistribution 中生成随机变量：

比较直方图与边缘分布的概率密度函数的图线：

估计分布参数：

定义三变量的概率分布：

求边缘分布：

求 的协方差矩阵：

边缘分布的方差形成了 的协方差矩阵的对角线：

参数分布  (2)

许多多变量参数分布的边缘分布自动化简：

单变量边缘分布服从 BetaDistribution：

多变量边缘分布服从 DirichletDistribution：

在某些情况下，边缘分布不会自动化简：

单变量边缘分布化简为一个 BinomialDistribution：

多变量边缘分布不化简：

所得的边缘分布仍然可以以类似其它分布的方式使用：

非参数分布  (3)

求 EmpiricalDistribution 的边缘分布：

边缘分布的累积分布函数：

求 SmoothKernelDistribution 的边缘分布：

求 HistogramDistribution 的边缘分布：

与各分量的直方图比较：

导出分布  (9)

求 MarginalDistribution 的边缘分布：

的第二个边缘分布是 的第三个边缘分布：

求 CopulaDistribution 的边缘分布：

求 TruncatedDistribution 的边缘分布：

概率密度函数：

求 MixtureDistribution 的边缘分布：

每个边缘分布是边缘分布的混合：

与各分量的边缘分布比较：

MixtureDistribution 的边缘分布是边缘分布的混合：

绘制这两个边缘分布的概率密度函数：

利用边缘分布创建一个双变量分布：

比较原分布 的概率密度函数和边缘分布的 ProductDistribution：

比较协方差矩阵：

求 TransformedDistribution 的边缘分布：

求 ParameterMixtureDistribution 的边缘分布：

可视化概率密度函数：

求 OrderDistribution 的边缘分布：

概率密度函数：

均值：

方差：

一个 QuantityDistribution 的边缘分布给出 QuantityDistribution：

单变量边缘分布：

多变量边缘分布：

自动化简  (12)

离散参数分布  (3)

多变量 DiscreteUniformDistribution 的边缘分布服从一个均匀分布：

MultivariatePoissonDistribution 的单变量边缘分布服从 PoissonDistribution：

多变量边缘分布服从多变量泊松分布：

MultinomialDistribution 的单变量边缘分布服从 BinomialDistribution：

连续参数分布  (6)

BinormalDistribution 的边缘分布服从 NormalDistribution：

MultinormalDistribution 的所有单变量边缘分布服从 NormalDistribution：

MultinormalDistribution 的多变量边缘分布是多变量正态分布：

多变量 UniformDistribution 的边缘分布服从均匀分布：

DirichletDistribution 的一维边缘分布服从 BetaDistribution：

DirichletDistribution 的多变量边缘分布服从狄利克雷分布：

MultivariateTDistribution 的单变量边缘分布服从 StudentTDistribution：

LogMultinormalDistribution 的单变量边缘分布服从 LogNormalDistribution：

LogMultinormalDistribution 的多变量边缘分布服从对数多正态分布：

导出分布  (3)

ProductDistribution 的边缘分布是分量分布：

一维边缘分布：

二维边缘分布也由 ProductDistribution 定义：

CopulaDistribution 的单变量边缘分布是用于具体指定中的边缘分布：

MixtureDistribution 的边缘分布是各分量边缘分布的混合：

应用  (5)

可视化单变量边缘分布与双变量分布：

绘制单变量边缘分布：

把结果显示在一起：

一辆中型汽车的城市和高速公路油耗服从双正态分布. 求城市里程数分布：

绘制概率密度函数的图线：

求平均城市油耗：

男性的体重和身高服从双正态分布. 求身高的分布：

概率密度函数：

求男性身高的中位数：

求下四分位数：

以米为单位表示身高分布：

投掷一枚正反面出现概率相同的骰子三次，希望可以出现三个反面.求以第二次投掷或者第三次投掷时出现正面的形式失败的次数的联合分布：

概率密度函数：

求每种失败类型的平均数目：

求这两种失败类型都出现的总数：

模拟由于第二次或者第三次投掷出现正面而失败的次数：

一座大学校园完全位于双城 和 中. 平均说来，在校园内每天有10起交通事故，并且每天在这两个城市中发生的交通事故数目的联合分布为：

求每个城市中交通事故数目的分布：

比较概率密度函数：

模拟30天内 城中每天发生的交通事故的数目：

属性和关系  (5)

如果一个事件不依赖于所有变量，则使用边缘分布：

计算事件概率：

如果函数没有涉及所有变量，求期望：

一个 个变量的多变量分布具有 个适当的边缘分布：

边缘分布的累积分布函数可以通过求互补变量的极限获得：

计算 ，得到边缘累积分布函数 ：

计算 ，得到边缘累积分布函数 ：

一个边缘分布的概率密度函数可以通过对其余互补变量积分获得：

根据 计算边缘概率密度函数 ：

根据 计算边缘概率密度函数 ：

多变量边缘分布保持了分量之间的相关性：

求第一个分量和第三个分量的边缘分布：

边缘分布的协方差是子矩阵 ：

对于一个离散分布：

的协方差矩阵：

定义第二个分量和第三个分量的边缘分布：

的协方差是 的协方差的子矩阵：

巧妙范例  (1)

一个三元分布的全部边缘概率密度函数，共6种：

Wolfram Research (2010)，MarginalDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MarginalDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，MarginalDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MarginalDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "MarginalDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/MarginalDistribution.html.

APA

Wolfram 语言. (2010). MarginalDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MarginalDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_marginaldistribution, author="Wolfram Research", title="{MarginalDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MarginalDistribution.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_marginaldistribution, organization={Wolfram Research}, title={MarginalDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MarginalDistribution.html}, note=[Accessed: 17-November-2024 ]}