NArgMax[f,x]
gives a position xmax at which f is numerically globally maximized.
NArgMax[f,{x,y,…}]
gives a position {xmax,ymax,…} at which f is numerically globally maximized.
NArgMax[{f,cons},{x,y,…}]
gives a position at which f is numerically globally maximized subject to the constraints cons.
NArgMax[…,x∈reg]
constrains x to be in the region reg.




NArgMax
NArgMax[f,x]
gives a position xmax at which f is numerically globally maximized.
NArgMax[f,{x,y,…}]
gives a position {xmax,ymax,…} at which f is numerically globally maximized.
NArgMax[{f,cons},{x,y,…}]
gives a position at which f is numerically globally maximized subject to the constraints cons.
NArgMax[…,x∈reg]
constrains x to be in the region reg.
Details and Options



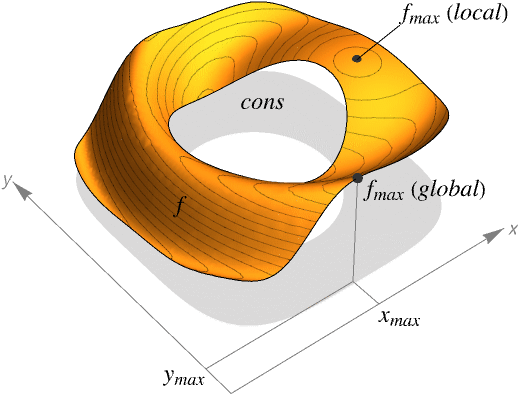
- NArgMax is also known as global optimization (GO).
- NArgMax always attempts to find a global maximum of f subject to the constraints given.
- NArgMax is typically used to find the largest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
- NArgMax returns a list of the form {xmin,ymin,…}.
- NArgMax[…,{x,y,…}] is effectively equivalent to {x,y,…}/.Last[NMaximize[…,{x,y,…},…].
- If f is linear or concave and cons are linear or convex, the result given by NArgMax will be the global maximum, over both real and integer values; otherwise, the result may sometimes only be a local maximum.
- If NArgMax determines that the constraints cannot be satisfied, it returns {Indeterminate,…}.
- NArgMax supports a modeling language where the objective function f and constraints cons are given in terms of expressions depending on scalar or vector variables. f and cons are typically parsed into very efficient forms, but as long as f and the terms in cons give numerical values for numerical values of the variables, NArgMax can often find a solution.
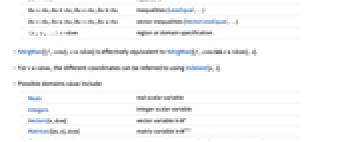
- The constraints cons can be any logical combination of:
-
lhs==rhs equations lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs inequalities (LessEqual, …) lhsrhs, lhsrhs, lhsrhs, lhsrhs vector inequalities (VectorLessEqual, …) {x,y,…}∈rdom region or domain specification - NArgMax[{f,cons},x∈rdom] is effectively equivalent to NArgMax[{f,cons&&x∈rdom},x].
- For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
- Possible domains rdom include:
-
Reals real scalar variable Integers integer scalar variable Vectors[n,dom] vector variable in 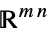
Matrices[{m,n},dom] matrix variable in 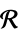
ℛ vector variable restricted to the geometric region 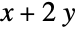
- By default, all variables are assumed to be real.
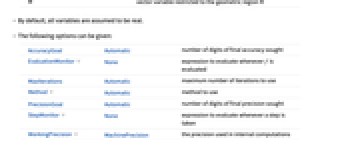
- The following options can be given:
-
AccuracyGoal Automatic number of digits of final accuracy sought EvaluationMonitor None expression to evaluate whenever f is evaluated MaxIterations Automatic maximum number of iterations to use Method Automatic method to use PrecisionGoal Automatic number of digits of final precision sought StepMonitor None expression to evaluate whenever a step is taken WorkingPrecision MachinePrecision the precision used in internal computations - The settings for AccuracyGoal and PrecisionGoal specify the number of digits to seek in both the value of the position of the maximum and the value of the function at the maximum.
- NArgMax continues until either of the goals specified by AccuracyGoal or PrecisionGoal is achieved.
- The methods for NArgMax fall into two classes. The first class of guaranteed methods uses properties of the problem so that, when the method converges, the maximum found is guaranteed to be global. The second class of heuristic methods uses methods that may include multiple local searches, commonly adjusted by some stochasticity, to home in on a global maximum. These methods often do find the global maximum, but are not guaranteed to do so.
- Methods that are guaranteed to give a global maximum when they converge to a solution include:
-
"Convex" use only convex methods "MOSEK" use the commercial MOSEK library for convex problems "Gurobi" use the commercial Gurobi library for convex problems "Xpress" use the commercial Xpress library for convex problems - Heuristic methods include:
-
"NelderMead" simplex method of Nelder and Mead "DifferentialEvolution" use differential evolution "SimulatedAnnealing" use simulated annealing "RandomSearch" use the best local minimum found from multiple random starting points "Couenne" use the Couenne library for non-convex mixed-integer nonlinear problems
Examples
open all close allBasic Examples (4)
Scope (35)
Basic Uses (12)
Maximize ![]() subject to constraints
subject to constraints ![]() :
:
Several linear inequality constraints can be expressed with VectorGreaterEqual:
Use ![]() v>=
v>=![]() or \[VectorGreaterEqual] to enter the vector inequality sign :
or \[VectorGreaterEqual] to enter the vector inequality sign :
An equivalent form using scalar inequalities:
The inequality ![]() may not be the same as
may not be the same as ![]() due to possible threading in
due to possible threading in ![]() :
:
To avoid unintended threading in ![]() , use Inactive[Plus]:
, use Inactive[Plus]:
Use constant parameter equations to avoid unintended threading in ![]() :
:
VectorGreaterEqual represents a conic inequality with respect to the "NonNegativeCone":
To explicitly specify the dimension of the cone, use {"NonNegativeCone",n}:
Maximize ![]() subject to the constraint
subject to the constraint ![]() :
:
Specify the constraint ![]() using a conic inequality with "NormCone":
using a conic inequality with "NormCone":
Maximize the function ![]() subject to the constraint
subject to the constraint ![]() :
:
Use Indexed to access components of a vector variable, e.g. ![]() :
:
Use Vectors[n,dom] to specify the dimension and domain of a vector variable when it is ambiguous:
Specify non-negative constraints using NonNegativeReals (![]() ):
):
An equivalent form using vector inequality ![]() :
:
Specify non-positive constraints using NonPositiveReals (![]() ):
):
An equivalent form using vector inequalities:
Or constraints can be specified:
Domain Constraints (4)
Specify integer domain constraints using Integers:
Specify integer domain constraints on vector variables using Vectors[n,Integers]:
Specify non-negative integer domain constraints using NonNegativeIntegers (![]() ):
):
Specify non-positive integer domain constraints using NonPositiveIntegers (![]() ):
):
Region Constraints (5)
Find the maximum possible distance between two points that are constrained to be in two different regions:
Find the maximum ![]() such that the triangle and ellipse still intersect:
such that the triangle and ellipse still intersect:
Find the circle of maximum radius that contains the given three points:
Using Circumsphere gives the same result directly:
Linear Problems (5)
With linear objectives and constraints when a maximum is found, it is global:
The constraints can be equality and inequality constraints:
Use Equal to express several equality constraints at once:
An equivalent form using several scalar equalities:
Use VectorLessEqual to express several LessEqual inequality constraints at once:
Use ![]() v<=
v<=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
An equivalent form using scalar inequalities:
Use Interval to specify bounds on a variable:
Convex Problems (3)
Use "NonNegativeCone" to specify linear functions of the form ![]() :
:
Use ![]() v>=
v>=![]() to enter the vector inequality in a compact form:
to enter the vector inequality in a compact form:
Maximize ![]() such that
such that ![]() is positive semidefinite:
is positive semidefinite:
Show the maximizer on a plot of the objective function:
Maximize the concave objective function ![]() such that
such that ![]() is positive semidefinite and
is positive semidefinite and ![]() :
:
Transformable to Convex (3)
Maximize the quasi-concave function ![]() subject to inequality and norm constraints. The objective is quasi-concave because it is a product of two non-negative affine functions:
subject to inequality and norm constraints. The objective is quasi-concave because it is a product of two non-negative affine functions:
The maximization is solved by minimizing the negative of the objective, ![]() , that is quasi-convex. Quasi-convex problems can be solved as a parametric convex optimization problem for the parameter
, that is quasi-convex. Quasi-convex problems can be solved as a parametric convex optimization problem for the parameter ![]() :
:
Plot the objective as a function of the level-set ![]() :
:
For a level-set value between the interval ![]() , the smallest objective is found:
, the smallest objective is found:
The problem becomes infeasible when the level-set value is increased:
Maximize ![]() subject to the constraint
subject to the constraint ![]() . The objective is not convex but can be represented by a difference of convex function
. The objective is not convex but can be represented by a difference of convex function ![]() where
where ![]() and
and ![]() are convex functions:
are convex functions:
Plot the region and the minimizing point:
Maximize ![]() subject to the constraints
subject to the constraints ![]() . The constraint
. The constraint ![]() is not convex but can be represented by a difference of convex constraint
is not convex but can be represented by a difference of convex constraint ![]() where
where ![]() and
and ![]() are convex functions:
are convex functions:
Options (7)
AccuracyGoal & PrecisionGoal (2)
This enforces convergence criteria ![]() and
and ![]() :
:
This enforces convergence criteria ![]() and
and ![]() , which is not achievable with the default machine-precision computation:
, which is not achievable with the default machine-precision computation:
Setting a high WorkingPrecision makes the process convergent:
EvaluationMonitor (1)
Method (2)
Some methods may give suboptimal results for certain problems:
The automatically chosen method gives the optimal solution for this problem:
The automatic method choice for this nonconvex problem is method "Couenne":
Plot the objective function along with the global maximum point:
Use method "NelderMead" for problems with many variables when speed is essential:
StepMonitor (1)
Steps taken by NArgMax in finding the maximum of a function:
WorkingPrecision (1)
With the working precision set to ![]() , by default AccuracyGoal and PrecisionGoal are set to half of the working precision:
, by default AccuracyGoal and PrecisionGoal are set to half of the working precision:
Applications (8)
Geometry Problems (4)
Find the half-lengths of the principal axes ![]() that maximize the volume of an ellipsoid with a surface area of at most 1:
that maximize the volume of an ellipsoid with a surface area of at most 1:
The surface area can be approximated by:
Maximize the volume area by minimizing its reciprocal:
This is the sphere. Including additional constraints on the axes lengths changes this:
Find the analytic center of a convex polygon. The analytic center is a point that maximizes the product of distances to the constraints:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
The objective is to maximize ![]() . Since the logarithm function is monotonic, this is equivalent to maximizing
. Since the logarithm function is monotonic, this is equivalent to maximizing ![]() :
:
Solve the unconstrained problem:
Visualize the location of the center:
Find the maximum-area ellipse parametrized as ![]() that can be fitted into a convex polygon:
that can be fitted into a convex polygon:
Each segment of the convex polygon can be represented as intersections of half-planes ![]() . Extract the linear inequalities:
. Extract the linear inequalities:
Applying the parametrization to the half-planes gives ![]() . The term
. The term ![]() . Thus, the constraints are
. Thus, the constraints are ![]() :
:
Maximizing the area is equivalent to maximizing ![]() :
:
Convert the parametrized ellipse into the explicit form as ![]() :
:
Find the largest radius ![]() for
for ![]() non-overlapping circles and their centers that can be contained in a
non-overlapping circles and their centers that can be contained in a ![]() square. The box constraint can be represented as
square. The box constraint can be represented as ![]() :
:
Find the maximum radius ![]() and the circle centers
and the circle centers ![]() :
:
Portfolio Optimization (1)
Find the distribution of capital ![]() to invest in six stocks to maximize return while minimizing risk:
to invest in six stocks to maximize return while minimizing risk:
The return is given by ![]() , where
, where ![]() is a vector of expected return value of each individual stock:
is a vector of expected return value of each individual stock:
The risk is given by ![]() ;
; ![]() is a risk-aversion parameter and
is a risk-aversion parameter and ![]() :
:
The objective is to maximize return while minimizing risk for a specified risk-aversion parameter:
The effect on market prices of stocks due to the buying and selling of stocks is modeled by ![]() , which is modeled by a power cone using the epigraph transformation:
, which is modeled by a power cone using the epigraph transformation:
The weights ![]() must all be greater than 0 and the weights plus market impact costs must add to 1:
must all be greater than 0 and the weights plus market impact costs must add to 1:
Compute the returns and corresponding risk for a range of risk-aversion parameters:
The optimal ![]() over a range of
over a range of ![]() gives an upper-bound envelope on the tradeoff between return and risk:
gives an upper-bound envelope on the tradeoff between return and risk:
Compute the weights for a specified number of risk-aversion parameters:
By accounting for the market costs, a diversified portfolio can be obtained for low risk aversion, but when the risk aversion is high, the market impact cost dominates, due to purchasing a less diversified stock:
Investment Problems (2)
Find the allocation of a maximum of $250,000 of capital to purchase two stocks and a bond such that the return on investment is maximized. Let ![]() be the amount to invest in the two stocks and let
be the amount to invest in the two stocks and let ![]() be the amount to invest in the bond:
be the amount to invest in the bond:
The amount invested in the utilities stock cannot be more than $40,000:
The amount invested in the bond must be at least $70,000:
The total amount invested in the two stocks must be at least half the total amount invested:
The stocks pay a annual dividend of 9% and 4%, respectively. The bond pays a dividend of 5%. The total return on investment is:
The cost with purchasing the stocks and bonds and executing the transactions is ![]() :
:
The optimal amount to be invested can be found by maximizing the profit while minimizing cost:
The total amount invested and the annual dividends received from the investments are:
Find the optimal combination of investments that yields maximum profit. The net present value and the costs associated with each investment are:
Let ![]() be a decision variable such that
be a decision variable such that ![]() if investment
if investment ![]() is selected. The objective is to maximize profits while minimizing costs:
is selected. The objective is to maximize profits while minimizing costs:
There is a maximum $14,000 available for investing:
Solve the maximization problem to get the optimal combination of investments:
Traveling Salesman Problem (1)
Find the path that a salesman should take through ![]() cities such that each city is only visited once, travel cost savings are maximized and distance traveled is minimized. Generate the locations:
cities such that each city is only visited once, travel cost savings are maximized and distance traveled is minimized. Generate the locations:
Let ![]() be the distance between city
be the distance between city ![]() and city
and city ![]() . Let
. Let ![]() be a decision variable such that if
be a decision variable such that if ![]() , the path goes from city
, the path goes from city ![]() to city
to city ![]() :
:
The travel budget to go from one city to another is $15. If two cities are are within 50 miles, the salesman pays $5, and otherwise pays a $10 flat rate. The total savings are:
The objective is to maximize savings while minimizing distance:
The salesman can arrive from exactly one city and can depart to exactly one other city:
The salesman cannot arrive in one city and depart to the same city:
The salesman must travel to all the locations in a single tour:
The decision variable is a binary variable and the dummy variable is ![]() :
:
Properties & Relations (5)
NMaximize gives the maximum value and rules for the maximizing values of the variables:
NArgMax gives a list of the maximizing values:
NMaxValue gives only the maximum value:
Maximizing a function f is equivalent to minimizing -f:
For convex problems, ConvexOptimization may be used to obtain additional solution properties:
For convex problems with parameters, using ParametricConvexOptimization gives a ParametricFunction:
The ParametricFunction may be evaluated for values of the parameter:
Define a function for the parametric problem using NArgMax:
Compare the speed of the two approaches:
Derivatives of the ParametricFunction can also be computed:
For convex problems with parametric constraints, RobustConvexOptimization finds an optimum that works for all possible values of the parameters:
NArgMax may find a maximizer that gives a smaller maximum value for particular values of the parameters:
This minimizer does not satisfy the constraints for all allowed values of ![]() and
and ![]() :
:
The maximum value found for particular values of the parameters is greater than or equal to the robust minimum:
Related Guides
History
Introduced in 2008 (7.0) | Updated in 2014 (10.0) ▪ 2021 (12.3) ▪ 2021 (13.0) ▪ 2022 (13.2) ▪ 2024 (14.1)
Text
Wolfram Research (2008), NArgMax, Wolfram Language function, https://reference.wolfram.com/language/ref/NArgMax.html (updated 2024).
CMS
Wolfram Language. 2008. "NArgMax." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/NArgMax.html.
APA
Wolfram Language. (2008). NArgMax. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NArgMax.html
BibTeX
@misc{reference.wolfram_2025_nargmax, author="Wolfram Research", title="{NArgMax}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NArgMax.html}", note=[Accessed: 20-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_nargmax, organization={Wolfram Research}, title={NArgMax}, year={2024}, url={https://reference.wolfram.com/language/ref/NArgMax.html}, note=[Accessed: 20-February-2026]}