NDSolveValue

NDSolveValue[eqns,expr,{x,xmin,xmax}]

gives the value of expr with functions determined by a numerical solution to the ordinary differential equations eqns with the independent variable x in the range xmin to xmax.

NDSolveValue[eqns,expr,{x,xmin,xmax},{y,ymin,ymax}]

solves the partial differential equations eqns over a rectangular region.

NDSolveValue[eqns,expr,{x,y}∈Ω]

solves the partial differential equations eqns over the region Ω.

NDSolveValue[eqns,u,{t,tmin,tmax},{x,y}∈Ω]

solves the time-dependent partial differential equations eqns over the region Ω.

Details and Options

  • NDSolveValue[eqns,y[x],{x,xmin,xmax}] gives solutions for y[x] rather than for the function y itself.
  • Differential equations must be stated in terms of derivatives such as y'[x], obtained with D, not total derivatives obtained with Dt.
  • Partial differential equations may also be specified using the differential operators Grad (∇), Div (∇.), Laplacian (∇2), and Curl (∇). Typically these operators are used as in Inactive[op] to keep the operator form from evaluating.
  • NDSolveValue solves a wide range of ordinary differential equations as well as many partial differential equations.
  • NDSolveValue can also solve many delay differential equations.
  • In ordinary differential equations, the functions yi must depend only on the single variable x. In partial differential equations, they may depend on more than one variable.
  • The differential equations must contain enough initial or boundary conditions to determine the solutions for the yi completely.
  • Initial and boundary conditions are typically stated in the form y[x0]==c0, y'[x0]==dc0, etc., but may consist of more complicated equations.
  • The c0, dc0, etc. can be lists, specifying that y[x] is a function with vector or general list values.
  • Periodic boundary conditions can be specified using y[x0]==y[x1].
  • The point x0 that appears in the initial or boundary conditions need not lie in the range xmin to xmax over which the solution is sought.
  • In delay differential equations, initial history functions are given in the form y[x/;x<x0]==c0, where c0 is in general a function of x.
  • WhenEvent[event,action] may be included in the equations eqns to specify an action that occurs when event becomes True.
  • Boundary values may also be specified using DirichletCondition and NeumannValue.
  • The differential equations in NDSolveValue can involve complex numbers.
  • NDSolveValue can solve many differential‐algebraic equations, in which some of the eqns are purely algebraic, or some of the variables are implicitly algebraic.
  • The yi can be functions of the dependent variables, and need not include all such variables.
  • The following options can be given:
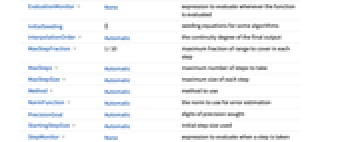
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    CompiledAutomaticwhether expressions should be compiled automatically
    DependentVariables Automaticthe list of all dependent variables
    EvaluationMonitor Noneexpression to evaluate whenever the function is evaluated
    InitialSeeding{}seeding equations for some algorithms
    InterpolationOrder Automaticthe continuity degree of the final output
    MaxStepFraction 1/10maximum fraction of range to cover in each step
    MaxSteps Automaticmaximum number of steps to take
    MaxStepSize Automaticmaximum size of each step
    Method Automaticmethod to use
    NormFunction Automaticthe norm to use for error estimation
    PrecisionGoalAutomaticdigits of precision sought
    StartingStepSize Automaticinitial step size used
    StepMonitor Noneexpression to evaluate when a step is taken
    WorkingPrecision MachinePrecisionprecision to use in internal computations
  • NDSolveValue adapts its step size so that the estimated error in the solution is just within the tolerances specified by PrecisionGoal and AccuracyGoal.
  • The option NormFunction->f specifies that the estimated errors for each of the yi should be combined using f[{e1,e2,…}].
  • AccuracyGoal effectively specifies the absolute local error allowed at each step in finding a solution, while PrecisionGoal specifies the relative local error.
  • If solutions must be followed accurately when their values are close to zero, AccuracyGoal should be set larger, or to Infinity.
  • The default setting of Automatic for AccuracyGoal and PrecisionGoal is equivalent to WorkingPrecision/2.
  • The default setting of Automatic for MaxSteps estimates the maximum number of steps to be taken by NDSolve, depending on start and stop time and an estimate of the step size. Should this not be possible, a fixed number of steps is taken.
  • The setting for MaxStepFraction specifies the maximum step to be taken by NDSolve as a fraction of the range of values for each independent variable.
  • With DependentVariables->Automatic, NDSolve attempts to determine the dependent variables by analyzing the equations given.
  • NDSolveValue typically solves differential equations by going through several different stages depending on the type of equations. With Method->{s1->m1,s2->m2,…}, stage si is handled by method mi. The actual stages used and their order are determined by NDSolve, based on the problem to solve.
  • Possible solution stages are:
  • "TimeIntegration"time integration for systems of differential equations
    "BoundaryValues"ordinary differential equation boundary value solutions
    "DiscontinuityProcessing"symbolic processing for handling of discontinuous differential equations
    "EquationSimplification"simplification of equation form for numerical evaluation
    "IndexReduction"symbolic index reduction for differential algebraic equations
    "DAEInitialization"consistent initialization for differential algebraic equations
    "PDEDiscretization"discretization for partial differential equations
  • With Method->m1 or Method->{m1,s2->m2,…}, the method m1 is assumed to be for time integration, so Method->m1 is equivalent to Method->{"TimeIntegration"->m1}.
  • Possible explicit time integration settings for the Method option include:
  • "Adams"predictor‐corrector Adams method with orders 1 through 12
    "BDF"implicit backward differentiation formulas with orders 1 through 5
    "ExplicitRungeKutta"adaptive embedded pairs of 2(1) through 9(8) Runge–Kutta methods
    "ImplicitRungeKutta"families of arbitrary‐order implicit Runge–Kutta methods
    "SymplecticPartitionedRungeKutta"interleaved Runge–Kutta methods for separable Hamiltonian systems
  • With Method->{"controller",Method->"submethod"} or Method->{"controller",Method->{m1,m2,…}}, possible controller methods include:
  • "Composition"compose a list of submethods
    "DoubleStep"adapt step size by the double‐step method
    "EventLocator"respond to specified events
    "Extrapolation"adapt order and step size using polynomial extrapolation
    "FixedStep"use a constant step size
    "OrthogonalProjection"project solutions to fulfill orthogonal constraints
    "Projection"project solutions to fulfill general constraints
    "Splitting"split equations and use different submethods
    "StiffnessSwitching"switch from explicit to implicit methods if stiffness is detected
  • Methods used mainly as submethods include:
  • "ExplicitEuler"forward Euler method
    "ExplicitMidpoint"midpoint rule method
    "ExplicitModifiedMidpoint"midpoint rule method with Gragg smoothing
    "LinearlyImplicitEuler"linearly implicit Euler method
    "LinearlyImplicitMidpoint"linearly implicit midpoint rule method
    "LinearlyImplicitModifiedMidpoint"linearly implicit Bader‐smoothed midpoint rule method
    "LocallyExact"numerical approximation to locally exact symbolic solution
  • The setting InterpolationOrder->All specifies that NDSolve should generate solutions that use interpolation of the same order as the underlying method used. »

Examples

open allclose all

Basic Examples  (7)

Solve a first-order ordinary differential equation:

Use the solution in a plot:

Use the function and its derivative in a plot:

Find specific values:

NDSolveValue can also directly return the above values:

Second-order nonlinear ordinary differential equation:

Plot the function and its first two derivatives:

Alternatively, substitute the functions to plot directly into NDSolveValue:

System of ordinary differential equations:

This solves the heat equation in one dimension:

Alternative form of equation:

Solve the Poisson equation over a Disk:

Find a minimal surface over a Disk with a sinusoidal boundary condition:

Solve a coupled nonlinear sine-Gordon equation over a region:

Scope  (25)

Ordinary Differential Equations  (7)

Specify any order equation; reduction to normal form is done automatically:

Directly differentiate the solution to make a phase plot:

Directly specify a system of equations:

Solve for a vector-valued function:

Plot the four components of the solution:

Different equivalent ways of specifying a harmonic oscillator as a second-order equation:

As a system of first-order equations:

Using a vector variable with the dimension deduced from the initial condition:

Use matrix-valued variables to compute the fundamental matrix solution:

Compare to the exact solution:

Define a Van der Pol equation:

The solution's "stiff" behavior that the default solver automatically handles:

Other methods may not be able to solve this system:

The solution ysol[x] is continuous, as it integrates the piecewise function once:

The solution ysol[x] is differentiable, whereas ysol'[x] is continuous only:

Partial Differential Equations  (5)

Nonlinear advection-diffusion equation in one dimension:

Define a system of PDEs of mixed parabolic-hyperbolic type:

Nonlinear sine-Gordon equation in two spatial dimensions with periodic boundary conditions:

Plot the solution at the final time:

Plot the time evolution of a radial cross section of the solution:

Solve a wave equation over a region with a slit:

Solve a Poisson equation with periodic boundary conditions on curved boundaries:

Visualize the solution:

Boundary Value Problems  (5)

A nonlinear multipoint boundary value problem:

Solve a nonlinear diffusion equation with Dirichlet and Neumann boundary conditions starting from an initial seed of :

Visualize the result:

Solve a nonlinear equation with Dirichlet boundary conditions starting from an initial seed of :

Visualize the result:

Solve a complex-valued nonlinear reaction equation with Dirichlet boundary conditions;

Visualize the result:

Solve a boundary value problem with a nonlinear load term :

Visualize the result:

Delay Differential Equations  (2)

Solve a delay differential with two constant delays and initial history function :

Discontinuities are propagated from at intervals equal to the delays:

Investigate stability for a linear delay differential equation:

Hybrid and Discontinuous Systems  (5)

A differential equation with a discontinuous right-hand side:

A differential equation with multiple right-hand sides:

A differential equation whose right-hand side changes at regular time intervals:

Reflect a solution across the axis each time it crosses the negative axis:

Periodic solution with sliding mode:

Differential-Algebraic Equations  (1)

A differential equation with an algebraic constraint:

Generalizations & Extensions  (1)

The names of functions need not be symbols:

Options  (29)

AccuracyGoal and PrecisionGoal  (1)

Use defaults to solve a celestial mechanics equation with sensitive dependence on initial conditions:

Higher accuracy and precision goals give a different result:

Increasing the goals extends the correct solution further:

DependentVariables  (1)

Set up a very large system of equations:

Solve for all the dependent variables, but save only the solution for x1:

EvaluationMonitor  (2)

Total number of evaluations:

The distance between successive evaluations; negative distance means a rejected step:

InitialSeedings  (2)

Specify an initial seeding of 0 for a boundary value problem:

Specify an initial seeding that depends on a spatial coordinate:

InterpolationOrder  (1)

Use InterpolationOrder->All to get interpolation the same order as the method:

This is more time consuming than the default interpolation order used:

It is much better in between steps:

MaxStepFraction  (1)

Features with small relative size in the integration interval can be missed:

Use MaxStepFraction to ensure features are not missed, independent of interval size:

MaxSteps  (1)

Integration stops short of the requested interval:

More steps are needed to resolve the solution:

Plot the solution in the phase plane:

MaxStepSize  (2)

The default step control may miss a suddenly varying feature:

A smaller MaxStepSize setting ensures that NDSolveValue catches the feature:

Attempting to compute the number of positive integers less than misses several events:

Setting a small enough MaxStepSize ensures that none of the events are missed:

Method  (12)

TimeIntegration  (5)

Differences between values of at successive steps with the default solution method:

With an explicit Runge–Kutta method, the step size is changed more often:

Difference order of 8:

With a difference order of 3, the steps are much smaller:

Extrapolation tends to take very large steps:

BoundaryValues  (1)

Solve a boundary value problem:

With the default option, the method finds the trivial solution:

Specify different starting conditions for the "Shooting" method to find different solutions:

DiscontinuityProcessing  (1)

NDSolveValue automatically does processing for discontinuous functions like Sign:

If the processing is turned off, NDSolveValue may fail at the discontinuity point:

With some time integration methods, the solution may be very inaccurate:

An equivalent way to find the solution is to use "DiscontinuitySignature":

The solutions are effectively identical:

EquationSimplification  (1)

The solution cannot be completed because the square root function is not sufficiently smooth:

One solution can be found by forming a residual and solving as a DAE system:

The other solution branch can be given by specifying a consistent value of :

IndexReduction  (1)

An index 3 formulation of a constrained pendulum using index reduction:

The default method can only solve index 1 problems:

The problem resulting from symbolic index reduction can be solved:

Solve using reduction to index 0 and a projection method to maintain the constraints:

Plot implicit energy constraint for the two solutions at the time steps:

DAEInitialization  (1)

Use forward collocation for initialization to avoid problems with the Abs term at 0:

PDEDiscretization  (2)

Solutions of Burgers' equation may steepen, leading to numerical instability:

Specify a spatial discretization sufficiently fine to resolve the front:

After the front forms, the solution decays relatively rapidly:

Solve a time-dependent Schrödinger equation on a refined mesh:

Plot the higher-accuracy solution:

NormFunction  (1)

Plot the actual solution error when using different error estimation norms:

A plot of the best solution:

StartingStepSize  (1)

For a very large interval, a short-lived feature near the start may be missed:

Setting a sufficiently small step size to start with ensures that the input is not missed:

StepMonitor  (3)

Plot the solution at each point where a step is taken in the solution process:

Total number of steps involved in finding the solution:

Differences between values of at successive steps:

WorkingPrecision  (1)

Error in the solution to a harmonic oscillator over 100 periods:

When the working precision is increased, the local tolerances are correspondingly increased:

With a large working precision, sometimes the "Extrapolation" method is quite effective:

Applications  (15)

Duffing Equation  (2)

The solution depends strongly on initial conditions:

Lotka–Volterra Equations  (1)

The Lotka–Volterra predator-prey equations [more info]:

Phase plane plot:

Lorenz Equations  (1)

The Lorenz equations [more info]:

Gavrilov–Shilnikov Model  (1)

Look at the appearance of the blue sky catastrophe orbit:

Heat Equation  (2)

Simple model for soil temperature at depth with periodic heating at the surface:

Model a temperature field with a heat source in a rod:

Solve the PDE:

Visualize the solution:

More information about the heat equation and applicable boundary conditions can be found in the Heat Transfer tutorial and the Heat Transfer PDE models guide page.

Wave Equation  (1)

Simple wave evolution with periodic boundary conditions:

Plot the solution:

Wolfram's Nonlinear Wave Equation  (2)

Wolfram's nonlinear wave equation [more info]:

This solves a 2+1-dimensional version of the equation:

n-Body Problems  (1)

Reduced 3-body problem [more info]:

A formulation suitable for a number of different initial conditions:

Nonlinear Schrödinger Equation  (1)

A soliton profile perturbed by a periodic potential:

Mackey–Glass Equation  (1)

View solutions of the Mackey–Glass delay differential equation:

Acoustics Equation  (1)

Define model variables vars for a transient acoustic pressure field with model parameters pars:

Define initial conditions ics of a right-going sound wave :

Set up the equation with a sound hard boundary at the right end:

Solve the PDE:

Visualize the sound field in the time domain:

More information about the wave equation and acoustics boundary conditions can be found in the Acoustics in the Time Domain tutorial and the Acoustics PDE models guide page.

Mass Transport  (1)

Model a 1D chemical species transport through different material with a reaction rate in one. The right side and left side are subjected to a mass concentration and inflow condition, respectively:

del .(-d del c(x))+a c(x)^(︷^( mass transport model )) =|_(Gamma_(x=0))q(x)^(︷^( mass flux value ))

Set up the stationary mass transport model variables vars:

Set up a region :

Specify the mass transport model parameters species diffusivity and a reaction rate active in the region :

Specify a species flux boundary condition:

Specify a mass concentration boundary condition:

Set up the equation:

Solve the PDE:

Visualize the solution:

More information about the mass transport equation and boundary conditions can be found in the Mass Transport tutorial and the MassTransport PDE models guide page.

Properties & Relations  (9)

NDSolveValue gives the solution function, while NDSolve returns the result as a rule:

The following two are equivalent:

NDSolveValue can directly return the result of the solution function at a specified point:

With NDSolve:

NDSolveValue can directly return the solution evaluated at several points:

With NDSolve:

NDSolveValue can directly return the result of any expression involving the solution:

With NDSolve:

If an equation has multiple solutions, NDSolveValue will pick one:

NDSolve will get both solution branches:

Numerically compute values of an integral at different points in an interval:

For functions of the independent variable, NDSolve effectively gives an indefinite integral:

Finding an event is related to finding a root of a function of the solution:

Event location finds the root accurately and efficiently:

This gives as a function of for a differential equation:

Find a root of :

Solve the equivalent boundary value problem:

Use NDSolve as a solver for a SystemModel:

Plot variables from the simulation result:

Use SystemModel to model larger hierarchical models:

Plot the tank levels in the tank system over time:

Possible Issues  (12)

Many NDSolveValue messages have specific message reference pages implemented. See how to access them in the Understand Error Messages workflow.

Multiple Solutions  (1)

For equations with multiple solutions, NDSolveValue will return only one solution:

Use NDSolve to get all the solutions:

Numerical Error  (3)

The error tends to grow as one goes further from the initial conditions:

Find the difference between numerical and exact solutions:

Error for a nonlinear equation:

For high-order methods, the default interpolation may have large errors between steps:

Interpolation with the order corresponding to the method reduces the error between steps:

Differential Algebraic Equations  (2)

Here is a system of differential-algebraic equations:

Find the solution with :

NDSolveValue may change the specified initial conditions if it cannot find the solution with :

NDSolveValue is limited to index 1, but the solution with has index 2:

The default method may not be able to converge to the default tolerances:

With lower AccuracyGoal and PrecisionGoal settings, a solution is found:

The "StateSpace" time integration method can solve this with default tolerances:

Partial Differential Equations  (4)

A large collection of PDE models from various fields with extensive explanation can found in the PDE models overview.

Define a nonlinear PDE:

The spatial discretization is based on the initial value, which varies less than the final value:

By increasing the minimal number of spatial grid points, you can accurately compute the final value:

The plot demonstrates the onset of a spatially more complex solution:

Define a heat equation with an initial value that is a step function:

Discontinuities in the initial value may result in too many spatial grid points:

Setting the number of spatial grid points smaller results in essentially as good a solution:

Define a Laplace equation with initial values:

The solver only works for equations well posed as initial value (Cauchy) problems:

The ill-posedness shows up as numerical instability:

Boundary Value Problems  (1)

This finds a trivial solution of a boundary value problem:

You can find other solutions by giving starting conditions for the solution search:

Neat Examples  (1)

Solve a maze by solving a Laplace equation and computing the gradient of the solution:

Wolfram Research (2012), NDSolveValue, Wolfram Language function, https://reference.wolfram.com/language/ref/NDSolveValue.html (updated 2019).

Text

Wolfram Research (2012), NDSolveValue, Wolfram Language function, https://reference.wolfram.com/language/ref/NDSolveValue.html (updated 2019).

CMS

Wolfram Language. 2012. "NDSolveValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/NDSolveValue.html.

APA

Wolfram Language. (2012). NDSolveValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NDSolveValue.html

BibTeX

@misc{reference.wolfram_2024_ndsolvevalue, author="Wolfram Research", title="{NDSolveValue}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/NDSolveValue.html}", note=[Accessed: 11-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ndsolvevalue, organization={Wolfram Research}, title={NDSolveValue}, year={2019}, url={https://reference.wolfram.com/language/ref/NDSolveValue.html}, note=[Accessed: 11-December-2024 ]}