NDSolveValue

NDSolveValue[eqns,expr,{x,xmin,xmax}]

根据含有独立变量 x 的常微分方程 eqns 的数值解，给出函数表达式 expr 的值，其范围为 xmin 到 xmax.

NDSolveValue[eqns,expr,{x,xmin,xmax},{y,ymin,ymax}]

在矩形区域内求解偏微分方程 eqns.

NDSolveValue[eqns,expr,{x,y}∈Ω]

在区域 Ω 内求解偏微分方程 eqns.

NDSolveValue[eqns,u,{t,tmin,tmax},{x,y}∈Ω]

在区域 Ω 内求解时变偏微分方程 eqns.

更多信息和选项

  • NDSolveValue[eqns,y[x],{x,xmin,xmax}] 给出 y[x] 的解，而不是函数 y 本身.
  • 微分方程必须以导数例如 y'[x] 的形式说明，用 D 获得，而不是用 Dt 得到的总导数.
  • 可以用微分运算符 Grad (∇)、Div (∇.)、Laplacian (∇2) 和 Curl (∇) 来指定偏微分方程. 一般情况下，这些运算符像在 Inactive[op] 中一样，作为算子形式存在而不被计算.
  • NDSolveValue 求解广范围的常微分方程以及许多偏微分方程.
  • NDSolveValue 也可以求解许多时滞微分方程.
  • 在常微分方程中，函数 yi 必须只依赖于单个变量 x. 在偏微分方程中，它们可能依赖多个变量.
  • 微分方程必须包括足够的初始或边界条件，才能完全决定 yi 的解.
  • 初始和边界条件一般以形式 y[x0]==c0、y'[x0]==dc0 等给出，但可能由更复杂的方程组成.
  • c0、dc0 等可以是列表，指定 y[x] 是具有向量或通用列表值的函数.
  • 周期边界条件可用 y[x0]==y[x1] 指定.
  • 初始或边界条件中的 x0 不必位于求解范围 xmin 到 xmax.
  • 在时滞微分方程中，初始历史函数以 y[x/;x<x0]==c0 形式给出，其中 c0 一般是 x 的函数.
  • WhenEvent[event,action] 可能包含在方程 eqns 中，用来指定当 event 变成 True 时发生的 action.
  • 可以用 DirichletCondition 和 NeumannValue 来指定边界值.
  • NDSolveValue 中的微分方程可包含复数.
  • NDSolveValue 可求解许多微分代数方程组，某些 eqns 是纯代数的或某些变量是隐式代数.
  • yi 可以是因变量的函数，不需要包括所有这样的变量.
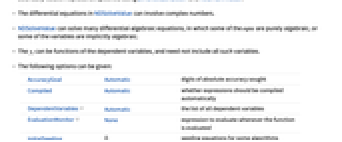
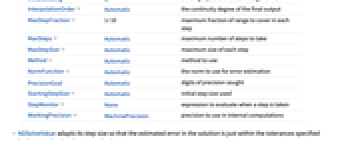
  • 可以给出以下选项：
  • AccuracyGoalAutomatic寻求的绝对精确数字
    CompiledAutomatic表达式是否应该自动编译
    DependentVariables Automatic所有相关变量的列表
    EvaluationMonitor None当计算函数时计算的的表达式
    InitialSeeding{}用于某些算法的播种方程
    InterpolationOrder Automatic最终输出的连续度
    MaxStepFraction 1/10每个步骤中最大的范围比例
    MaxSteps Automatic采用的最大步骤数
    MaxStepSize Automatic每一步的最大尺寸
    Method Automatic使用的方法
    NormFunction Automatic误差估计使用的范数
    PrecisionGoalAutomatic寻求的精确数字
    StartingStepSize Automatic使用的初始步骤大小
    StepMonitor None每采取步骤时计算的表达式
    WorkingPrecision MachinePrecision内部计算使用的精度
  • NDSolveValue 会调整它的步骤大小，因此解中的估计误差恰好在由 PrecisionGoal 和 AccuracyGoal 指定的公差之内.
  • 选项 NormFunction->f 指定每个 yi 的估计误差应使用 f[{e1,e2,…}] 组合.
  • AccuracyGoal 有效的指定在求解中每一步允许的绝对局部误差，其中 PrecisionGoal 指定相对局部误差.
  • 如果当解的值接近零时，必须准确求解的话，AccuracyGoal 应设为大一些，或为 Infinity.
  • AccuracyGoal 和 PrecisionGoal 的 Automatic 的默认设置等同于 WorkingPrecision/2.
  • MaxSteps 的默认设置 Automatic 根据开始和终止时间，以及每个步骤的大小，估计 NDSolve 所需的最大步骤数. 如果结果不可行，则采用固定步骤数.
  • MaxStepFraction 的设置指定由 NDSolve 采取的最大步骤，作为每个独立变量值的范围比例.
  • 当 DependentVariables->Automatic 时，NDSolve 通过分析给定的方程，试图决定相关变量.
  • NDSolveValue 一般通过依赖于方程类型的多个不同阶段求解微分方程. 当 Method->{s1->m1,s2->m2,…}，阶段 si 由方法 mi 处理. 实际使用的阶段和它们的顺序由基于要求解的问题的 NDSolve 决定.
  • 可能的求解阶段为：
  • "TimeIntegration"微分方程组的时间积分
    "BoundaryValues"常微分方程边界值解
    "DiscontinuityProcessing"处理不连续微分方程的符号式处理
    "EquationSimplification"数值计算的方程形式化简
    "IndexReduction"微分代数方程的符号索引化简
    "DAEInitialization"微分代数方程的一致初始化
    "PDEDiscretization"偏微分方程的离散化
  • 当 Method->m1 或 Method->{m1,s2->m2,…}，方法 m1 假设为时间积分，因此 Method->m1 等同于 Method->{"TimeIntegration"->m1}.
  • Method 选项的可能显式时间积分设置包括：
  • "Adams"预测-校正亚当斯法，阶数从1至12
    "BDF"隐式向后差分公式，阶数为1至5
    "ExplicitRungeKutta"2(1) 至 9(8) 自适应嵌入对龙格库塔法
    "ImplicitRungeKutta"任意阶数隐式龙格库塔法系列
    "SymplecticPartitionedRungeKutta"可分哈密顿系统的交错龙格库塔法s
  • 当 Method->{"controller",Method->"submethod"} 或Method->{"controller",Method->{m1,m2,…}}，可能的控制器方法包括：
  • "Composition"构成子方法的列表
    "DoubleStep"双步法自适应步骤尺寸
    "EventLocator"响应指定的事件
    "Extrapolation"使用多项式外推自适应阶数和步骤大小
    "FixedStep"使用常量步骤大小
    "OrthogonalProjection"满足正交约束的投影解
    "Projection"满足一般约束的投影解
    "Splitting"分开方程组和是哦那个不同的子方法
    "StiffnessSwitching"如果检测到刚度从显式切换到隐式
  • 主要用作子方法的方法包括：
  • "ExplicitEuler"向前欧拉方法
    "ExplicitMidpoint"中点规则方法
    "ExplicitModifiedMidpoint"具有 Gragg 平滑的中点规则法
    "LinearlyImplicitEuler"线性隐式欧拉方法
    "LinearlyImplicitMidpoint"线性隐式中点规则法
    "LinearlyImplicitModifiedMidpoint"线性隐式 Bader 平滑中点规则法
    "LocallyExact"数值近似到本地精确符号式解
  • 设置 InterpolationOrder->All 指定 NDSolve 应该产生使用与基本使用方法具有同样阶数的插值的解. »

范例

打开所有单元关闭所有单元

基本范例  (7)

求解一阶常微分方程：

在图中使用解：

在图中使用函数和它的导数：

求指定值：

NDSolveValue 也可以直接给出上述数值：

二阶非线性常微分方程：

绘制函数和它的两个导数：

或者将要绘制的函数直接代入 NDSolveValue：

常微分方程组：

以下求解一维热方程：

方程的其他形式：

求解 Disk 上的泊松方程：

求带有正弦边界条件 Disk 上的最小曲面：

求区域上耦合的非线性正弦-戈登方程：

范围  (25)

常微分方程组  (7)

指定任意阶方程；自动简化为正常形式：

直接对解求导数，绘制相位图：

直接指定方程组：

求解一个向量值函数：

绘制解的四个分量：

指定谐波振荡器为一个二阶方程的不同的方法：

作为一个一阶方程组：

使用一个向量变量，维数从初始条件中导出：

使用矩阵值变量计算基本的矩阵解：

比较精确解：

定义一个 Van der Pol 方程：

默认求解器会自动处理解的“僵硬”行为：

其他方法可能不能求解该方程组：

解 ysol[x] 是连续的，因为它对分段函数只进行一次积分：

解 ysol[x] 是可微的，然而 ysol'[x] 只是连续的：

偏微分方程组  (5)

一维非线性对流扩散方程：

定义混合抛物-双曲型的偏微分方程组：

具有周期性边界条件的两个空间维度的非线性正弦-Gordon 方程：

绘制最终时间的解：

绘制解的径向截面的时间演化：

求带有狭缝区域上的波动方程：

求解曲线边界上带有周期边界条件的泊松方程：

可视化结果：

边界值问题  (5)

非线性多点边界值问题：

求解非线性扩散方程 ，其中狄利克雷和诺伊曼条件开始于 的初始种子：

可视化结果：

求解非线性方程 ，其中狄利克雷和诺伊曼条件开始于 的初始种子：

可视化结果：

求解带有狄利克雷边界条件的复值非线性反应方程 ：

可视化结果：

求解带有非线性负荷项 的边界值问题：

可视化结果：

时滞微分方程  (2)

求解具有两个常量时滞和初始历史函数 的时滞微分：

不连续性在 以等于时滞的间隔传播：

研究线性时滞微分方程的稳定性：

混合及不连续系统  (5)

等式右边不连续的差分方程：

等式右边的值分为多段的差分方程：

等式右边在规则时间间隔时变化的微分方程：

每次当解穿过负 轴时，对其做关于 轴的映射：

具有滑动模式的周期解：

微分代数方程  (1)

具有代数约束的微分方程：

推广和延伸  (1)

函数名称不必是符号：

选项  (29)

AccuracyGoal 与 PrecisionGoal  (1)

使用默认设置求解对初始条件具有敏感依赖性的天体力学方程：

设定更高的准确度和精度给出不同的计算结果：

进一步提高准确度和精度以便更接近正确的解：

DependentVariables  (1)

设置一个很大的方程组：

求解所有相关变量，但只保存 x1 的解：

EvaluationMonitor  (2)

总计算次数：

连续计算间的距离；负距离意味被拒绝的步骤：

InitialSeedings  (2)

为边界值问题指定 0 的初始化种子：

指定依赖于空间坐标的初始化种子：

InterpolationOrder  (1)

使用 InterpolationOrder->All 获取与方法同样阶数的插值：

这比使用默认插值阶数更耗时：

步骤间更好：

MaxStepFraction  (1)

有可能错过积分区间中相对较小的特征：

使用 MaxStepFraction 确保不错过特征，和区间大小无关：

MaxSteps  (1)

由于所需区间不能满足，停止进行积分计算：

需要更多的步骤才能解得答案：

在相位平面绘制解：

MaxStepSize  (2)

默认步骤控制可能错过突然变化的特征：

更小的 MaxStepSize 设置保证 NDSolveValue 获取特征：

试图计算正整数小于 的数目会错过多个事件：

设置足够小的 MaxStepSize 保证不会错过任何事件：

Method  (12)

TimeIntegration  (5)

使用默认求解方法时，相邻步骤间 值的差异：

在显式龙格库塔法中，步骤大小改变的很频繁：

差分阶数为8：

差分阶数为3，步骤更小：

外推法（Extrapolation）趋向于采取很大的步骤：

BoundaryValues  (1)

求解边界值问题：

采用默认选项设置，得出的是平凡解：

为 "Shooting" 解法指定不同的起始条件来求出不同的解：

DiscontinuityProcessing  (1)

NDSolveValue 会自动处理像 Sign 这样的不连续函数：

如果相应的选项被设置为无效的话，碰到断点，NDSolveValue 可能会无法继续进行计算：

对于有些时间积分方法，求得的解会很不准确：

另一个办法是利用 "DiscontinuitySignature" 求解：

解实际上是一样的：

EquationSimplification  (1)

由于平方根函数不够平滑，无法求得全部的解：

通过形成残差，作为 DAE 求解，可以得到一个解：

通过指定一个统一的 的值，可以求得其它解：

IndexReduction  (1)

一个指数3的约束摆问题表述方程，需要用降指数方法：

默认解法只能求解指数1问题：

经过符号指数降阶处理的问题是可解的：

降阶为指数0并使用投影法以满足约束条件：

绘制两个解在时间步长上的隐式能量约束条件：

DAEInitialization  (1)

用前向配置法来初始化以避免在0点处有 Abs 项的问题：

PDEDiscretization  (2)

Bergers 方程的解可能会变陡，出现数值不稳定性问题：

指定足够精细的空间离散，求出前端：

前端形成之后，方程的解开始相对快速的衰减：

在细化网格上求解瞬态薛定谔方程：

绘制更高精度的解：

NormFunction  (1)

绘制使用不同误差估计范数情况下，实际解的误差：

最佳解的图：

StartingStepSize  (1)

对于很大的间隔，接近始端的短暂特征可能错过：

设置足够小的步骤尺寸来开始以保证不会错过输入：

StepMonitor  (3)

在解的过程中接受步骤的每个点上绘制解：

步骤总数包含在求解过程中：

连续步骤上 值间的差分：

WorkingPrecision  (1)

100个周期的谐波振荡器的解的误差：

当增加工作精度，局部公差相应增加：

具有大的工作精度，有时，"Extrapolation" 方法相当有效：

应用  (15)

Duffing 方程  (2)

解强烈依赖于初始条件：

Lotka–Volterra 方程组  (1)

Lotka–Volterra 猎物捕食方程 [更多信息]：

相位平面图：

Lorenz 方程组  (1)

Lorenz 方程组 [更多信息]:

Gavrilov–Shilnikov 模型  (1)

看蓝天灾变轨道的外观：

热方程  (2)

在具有定期表面加热，深度为 处的土壤温度的简单模型：

热源位于棒中，模拟温度场：

解 PDE：

可视化解：

有关热方程和适用的边界条件的更多信息，请参见 Heat Transfer 教程和 Heat Transfer PDE models 指南页面.

波方程  (1)

具有周期边界条件的简单波演化：

绘制解：

Wolfram 非线性波方程  (2)

Wolfram 非线性波方程 [更多信息]：

以下求解方程的 2+1-维度的版本：

n-体问题  (1)

简化的 3-体问题 [更多信息]：

公式化适于不同的初始条件数目：

非线性 Schrödinger 方程  (1)

被周期势能扰动的孤子轮廓：

Mackey–Glass 方程  (1)

查看 Mackey–Glass 时滞微分方程的解：

声学方程  (1)

定义瞬态声压场的模型变量 vars，模型参数为 pars：

定义向右传播的声波 的初始条件 ics：

设置方程，右侧为声硬边界条件：

解 PDE：

可视化时域中的声场：

有关波方程和声学边界条件的更多信息，请参见 Acoustics in the Time Domain 教程和 Acoustics PDE models 指南页面.

物质输运  (1)

给定化学物种在一种材料内的反应速率，模拟一维化学物种穿过不同材料的过程. 右侧和左侧分别受到质量浓度和流入条件的影响：

del .(-d del c(x))+a c(x)^(︷^( mass transport model )) =|_(Gamma_(x=0))q(x)^(︷^( mass flux value ))

设置稳态传质模型变量 vars：

设置区域 ：

指定传质模型参数物质扩散率 和在 区域中的反应速率 ：

指定物种通量边界条件：

指定质量浓度边界条件：

设置方程：

解 PDE：

可视化解：

有关物质输运方程和边界条件的更多信息，请参见 Mass Transport 教程和 MassTransport PDE models 指南页面.

属性和关系  (9)

NDSolveValue 给出解的函数，而 NDSolve 返回的结果是一个规则：

下述两个解是等价的：

NDSolveValue 可直接返回在指定点的解的函数：

来看 NDSolve：

NDSolveValue 可直接返回解在几个点的值：

来看 NDSolve：

NDSolveValue 可直接返回涉及解的任意表达式的结果：

来看 NDSolve：

如果一个方程有多个解，NDSolveValue 会选取其中一个：

NDSolve 则会同时求出两个解：

数值计算在一区间不同点的积分值：

具有独立变量的函数，NDSolve 有效地给出不定积分：

求事件与求解的函数的根相关：

事件位置准确和有效地找到根：

以下给出 作为微分方程 的函数：

求 的根：

求等边界值问题：

使用 NDSolve 作为 SystemModel 的一个求解器：

根据仿真结果绘制变量：

使用 SystemModel 模拟更大型的分层模型：

绘制随着时间的推移储罐系统中的储罐液位：

可能存在的问题  (12)

针对许多 NDSolveValue 消息，有特定的消息参考页面. 请到理解出错消息工作流程中了解怎样访问这些页面.

有多个解  (1)

对于有多个解的方程，NDSolveValue 只会返回一个解：

用 NDSolve 求得所有的解：

数值误差  (3)

当远离初始条件，误差趋于增长：

求数值和精确解间的不同：

非线性方程的误差：

对于高阶方法，默认插值在步骤间可能具有大的误差：

具有对应于方法的阶数的插值减少步骤间的误差：

微分代数方程  (2)

微分代数方程组：

，求方程的解：

设 ，如果还不能求出方程的解，NDSolveValue 可能会改变给定的初始条件：

NDSolveValue 只能求解指数1的方程，但是 时方程指数为2：

默认方法可能无法收敛于缺省容差：

把 AccuracyGoal 和 PrecisionGoal 设为较小的值以后，求出了一个解：

"StateSpace" 时间积分法可以在设置为缺省容差的情况下求出方程的解：

偏微分方程  (4)

在 PDE models overview 中可以找到各个领域的大量 PDE 模型以及详细的说明.

定义一个非线性 PDE：

空间离散化是基于初始值，它变化小于最终值：

通过增加空间网格点的最小数，你可以精确计算最终值：

图演示了一个空间更复杂解的开端：

定义一个热方程，初始值是一个阶跃函数：

初始值的不连续性可能导致太多的空间网格点：

设置更小的空间网格点基本上是一个好的解决方法：

定义具有初始值的拉普拉斯方程：

求解器只适用于具有良好初始值（柯西）问题的方程组：

不适定性显示为数值不稳定性：

边界值问题  (1)

以下求解边界值问题的平常解：

通过给出解搜索的起始条件，可以找到其它解：

巧妙范例  (1)

通过求解拉普拉斯方程并计算该解的梯度解开迷宫问题：

Wolfram Research (2012)，NDSolveValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NDSolveValue.html （更新于 2019 年）.

文本

Wolfram Research (2012)，NDSolveValue，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NDSolveValue.html （更新于 2019 年）.

CMS

Wolfram 语言. 2012. "NDSolveValue." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/NDSolveValue.html.

APA

Wolfram 语言. (2012). NDSolveValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NDSolveValue.html 年

BibTeX

@misc{reference.wolfram_2024_ndsolvevalue, author="Wolfram Research", title="{NDSolveValue}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/NDSolveValue.html}", note=[Accessed: 15-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ndsolvevalue, organization={Wolfram Research}, title={NDSolveValue}, year={2019}, url={https://reference.wolfram.com/language/ref/NDSolveValue.html}, note=[Accessed: 15-November-2024 ]}